SVPWM.rar_SVPWM doc_clark变换_clark变换与SVPWM_doc_空间矢量SVPWM

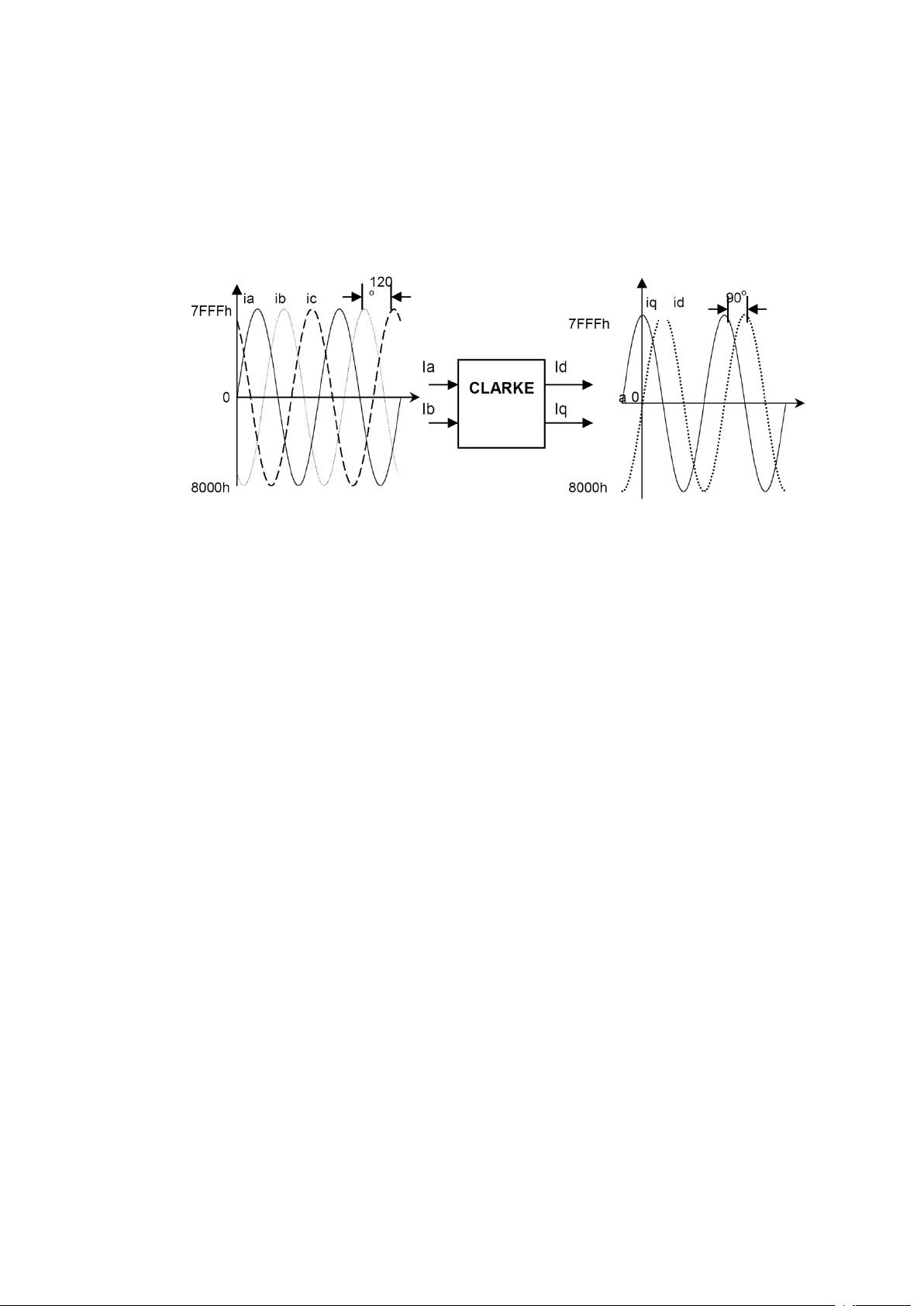
空间矢量脉宽调制（SVPWM，Space Vector Pulse Width Modulation）是一种高级的脉宽调制（PWM）技术，常用于电力电子设备，如电机驱动器和逆变器，以提高效率和功率密度。SVPWM的核心是将三相交流电转换为等效的直流磁场，然后通过优化脉冲宽度来模拟连续的直流电压，从而实现更平滑的输出波形，减少谐波失真。 在SVPWM中，Clark变换和Park变换是两个关键的数学转换工具，它们用于处理三相交流系统中的电压和电流。Clark变换是一种线性变换，它将三相交流系统的a、b、c相电压或电流转换为两相直轴（d）和交轴（q）坐标系的表示，这样可以简化后续的计算。 1. **Clark变换**：Clark变换的公式为： \[ \begin{bmatrix} V_d \\ V_q \\ V_0 \end{bmatrix} = \frac{1}{\sqrt{3}} \begin{bmatrix} 1 & 1 & 1 \\ -\frac{1}{2} & -\frac{1}{2} & \sqrt{3} \\ \frac{1}{2} & -\frac{1}{2} & -\sqrt{3} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix} \] 其中，\( V_d \) 和 \( V_q \) 分别代表直轴和交轴电压，\( V_0 \) 是星点电压，\( V_a \), \( V_b \), \( V_c \) 是三相电压。Clark变换将三相电压转换为对称两相坐标系，有助于消除零序分量，使得处理三相系统更为直观。 2. **Park变换**：在Clark变换之后，Park变换（也称为旋转变换）进一步将两相静止坐标系转换为旋转坐标系，通常以同步电机的转子速度为参考。Park变换公式为： \[ \begin{bmatrix} V_{d'} \\ V_{q'} \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} V_d \\ V_q \end{bmatrix} \] 其中，\( V_{d'} \) 和 \( V_{q'} \) 是旋转坐标系下的电压，\( \theta \) 是根据电机转子位置确定的角度。Park变换使得系统能够根据电机的实际运行状态进行动态控制。 在实际应用中，例如在"例1、CLARK变换的DSP实现"和"例2、PARK变换的DSP实现"中，这些变换通常由数字信号处理器（DSP）执行，因为它们需要快速精确的计算。DSP可以高效地执行这些复杂数学运算，并控制逆变器中的开关器件，以生成SVPWM所需的脉冲序列。 3. **空间矢量算法**：SVPWM算法的核心在于将每个开关周期划分为多个时间片，每个时间片对应一个特定的电压矢量。这些电压矢量在三相逆变器的六个开关状态之间切换，以尽可能接近理想的直流电压。在"例3、空间矢量的算法程序"中，可能包含的是实现这一过程的具体代码。 SVPWM技术结合了Clark变换和Park变换，通过优化脉宽调制策略，实现了高效的电机控制，降低了谐波影响，提高了系统性能。在现代电力电子和电机驱动领域，SVPWM是不可或缺的技术之一。