
混沌的概念:混沌(chaos)又称浑沌,人们通常
用它来描述混乱、杂乱无章、乱七八糟的状态,
在这个意义上它与无序的概念是相同的。
一、混沌的基本概念及特征

1.确定性
�� 在混沌系统中,描述系统演化的动力学方程的确定性
,是指方程(常微分方程、差分方程、时滞微分方程)是非
随机的,不含任何随机项。系统的未来(或过去)状态只与
初始条件及确定的演化规则有关,即系统的演化完全是由
内因决定的,与外在因素无关。这是至关重要的一条限制
,所以我们现在讲的混沌也叫“确定性混沌”。正因为确定
性的系统出现了复杂行为,也叫内随机性,人们才兴奋起
来,才一往倾心地钻研混沌。当然,从长远的观点来看,
人们肯定会研究带有随机项的更复杂系统的非周期运动。
然而,目前由于公众对混沌还有相当的误解,所以我们严
格区分是否为确定性至关重要,还不能笼统地从现象的层
次把一大堆似是而非的东西都称为混沌。总之,混沌概念
的狭义化总比泛化好些。现在我们考虑的混沌主要是一种
时间演化行为,不直接涉及空间分布变化,所以暂不考虑
偏微分方程。
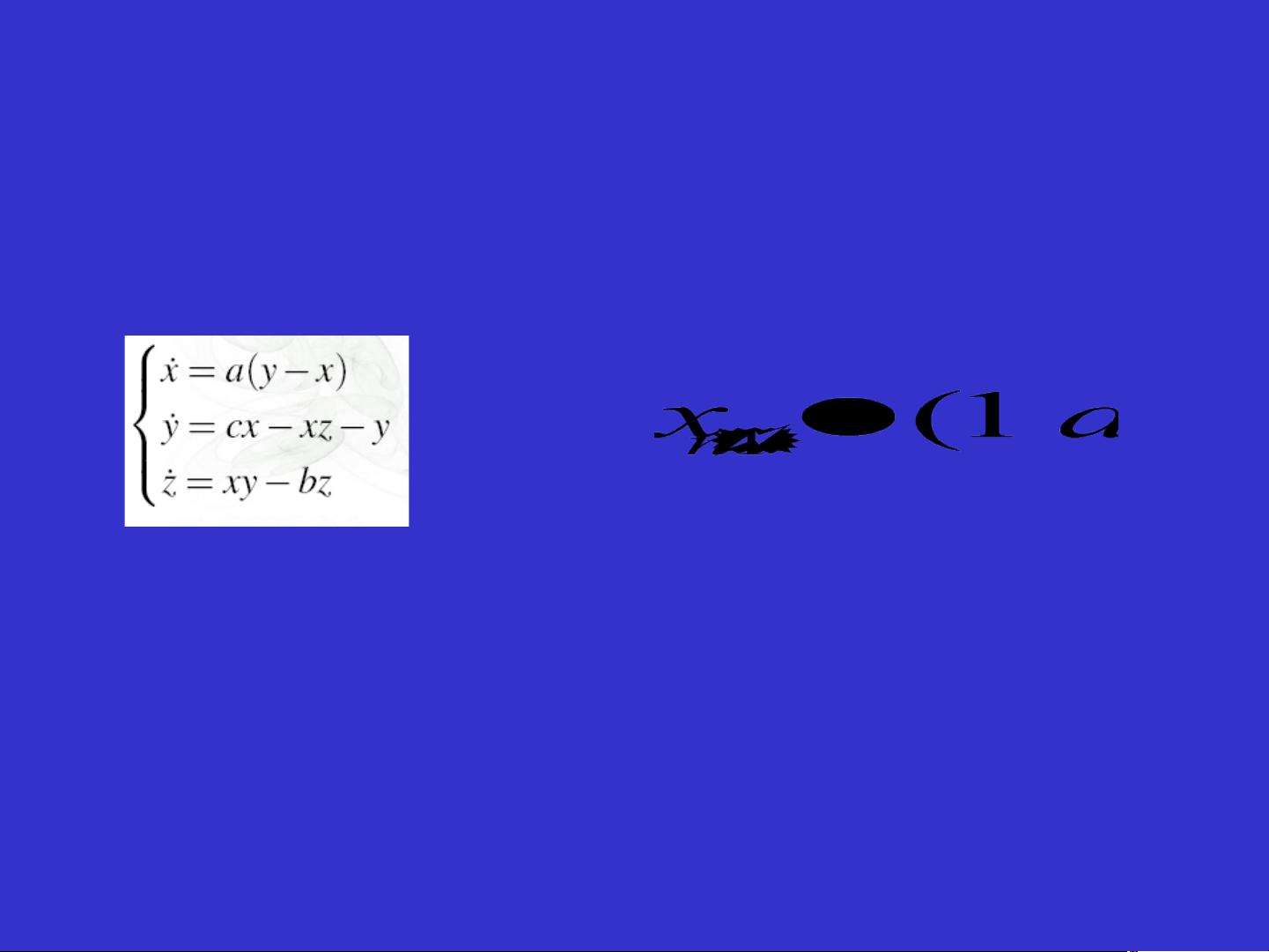
例:
Lorenz系统 Logistic 映射

2.非线性
�� 产生混沌的系统一定含有非线性因素,有了非线性未必产
生混沌,但没有非线性是肯定产生不了混沌的。也就是说,非
线性是产生混沌的必要条件。从功能上看,非线性是通过线性
来定义的,设G1和G2是任意两个(向量)函数,a和b是任意两个
常数,若算子乙满足如下叠加原理:
L(aGl+bG2) =aL(G1)+ bL(G2),
则称L是线性算子,否则L是非线性算子。包含非线性算子的系
统称为非线性系统。应当注意的是线性与非线性也不是绝对分
明的。对于某些复杂现象,在一定条件下,既可以把它视为非
线性现象也可以把它视为线性现象,这与人们看问题的角度和
所关心的变量的时空尺度不同有关。现在看来,非线性是普遍
存在的,多数问题不能通过线性的办法或线性化的办法来解决
,因而直接面对非线性是不可避免的。



















