BFGS.zip_BFGS的matlab程序_bfgs matlab_connecteddvb_swept6kc_拟牛顿

2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
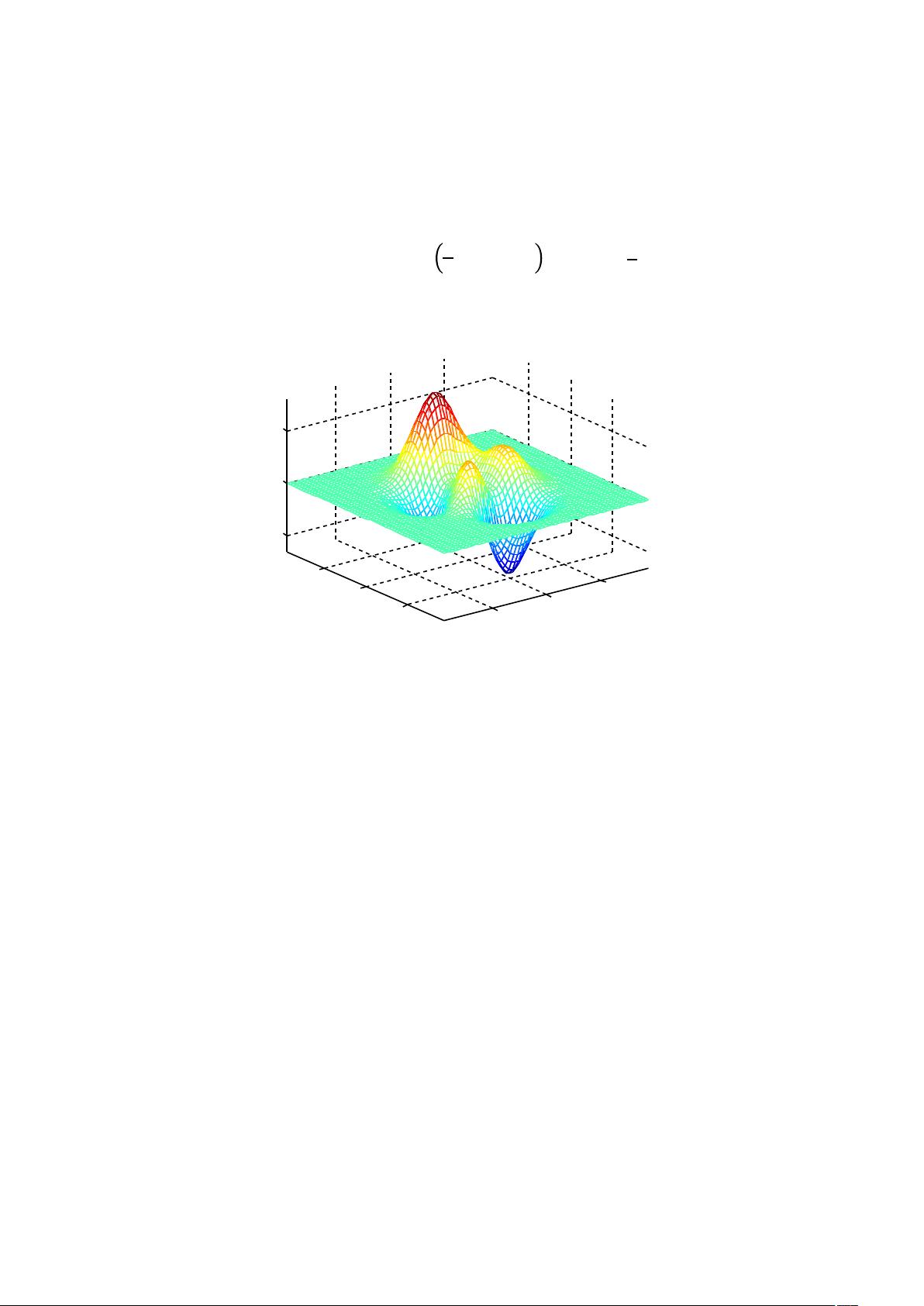
**拟牛顿法(BFGS)简介** 拟牛顿法是一种在优化领域广泛应用的迭代算法,主要用于求解无约束的连续二次可微函数的最小值问题。BFGS(Broyden-Fletcher-Goldfarb-Shanno)是拟牛顿法中最著名的一种,它在1970年由四位数学家提出,包括Broyden、Fletcher、Goldfarb和Shanno。BFGS算法基于梯度下降策略,并通过近似Hessian矩阵来改善搜索方向,使得在每一步迭代中能够更接近最优解。 **MATLAB中的BFGS实现** MATLAB是一个强大的数学计算软件,提供了许多内置的优化工具箱,其中包括了BFGS算法的实现。在MATLAB中使用BFGS算法,可以借助内置的`fminunc`函数,这是一个通用的无约束优化函数,它允许用户选择不同的优化算法,其中包括BFGS。用户需要提供目标函数和初始猜测值,`fminunc`会自动处理其余的细节,如迭代过程和Hessian矩阵的更新。 **MATLAB编程实现BFGS** 实现BFGS算法通常涉及以下几个关键步骤: 1. **目标函数定义**:你需要定义一个函数来表示你要优化的目标。这个函数应该返回一个标量值,表示当前点的目标函数值。 2. **梯度计算**:BFGS算法依赖于目标函数的梯度,因此你需要提供梯度函数的计算。这可以通过手动计算或者使用MATLAB的`gradient`函数自动计算。 3. **初始点选择**:选择一个合适的初始点作为优化的起始位置。 4. **调用BFGS算法**:使用MATLAB的`fminunc`函数,设置算法选项为'quasi-newton'或'BFGS',然后传入目标函数、梯度函数和初始点。 5. **迭代与结果分析**:`fminunc`会返回最优解的位置和目标函数的最小值。你可以根据返回的结果分析优化过程和结果的准确性。 **文件"connecteddvb"和"swept6kc"** 在提供的文件列表中,“connecteddvb”和“swept6kc”可能是特定的优化问题实例或者相关的辅助数据文件。这些文件可能包含了一些用于测试BFGS算法的示例问题,例如连接的双变量问题(Connected Double Variable Problem)或者某种特定的6节点电路模型(可能与“swept6kc”有关)。要理解这些文件的用途,你需要查看它们的内容,将它们与BFGS算法的实现相结合,以便在MATLAB环境中运行并验证算法的效果。 **总结** BFGS算法在MATLAB中的应用为解决优化问题提供了一个高效且实用的工具。通过理解BFGS的基本原理和MATLAB中的实现方法,我们可以利用这种强大的算法来解决各种实际的优化挑战。同时,结合具体的实例文件,可以进一步加深对算法性能和适用性的认识。
 BFGS.zip (2个子文件)
BFGS.zip (2个子文件)  BFGS
BFGS  bfgs3.m 981B
bfgs3.m 981B BFGS算法求解peaks函数极小值.docx 431KB
BFGS算法求解peaks函数极小值.docx 431KB- 1

- 粉丝: 86
- 资源: 1万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0