www.unicore.co.ua Unicore Systems Ltd. Page 1 of 17
FFT/IFFT 256 IP core
Pipelined FFT/IFFT 256 points (Fast Fourier Transform)
IP Core User Manual
G
G
E
E
N
N
E
E
R
R
A
A
L
L
I
I
N
N
F
F
O
O
R
R
M
M
A
A
T
T
I
I
O
O
N
N
The FFT256 User Manual contains description of the FFT256 core architecture to explain its
proper use.
FFT256 soft core is the unit to perform the Fast Fourier Transform (FFT). It performs one
dimensional 256 – complex point FFT. The data and coefficient widths are adjustable in the range
8 to 16.
F
F
E
E
A
A
T
T
U
U
R
R
E
E
S
S
Key features
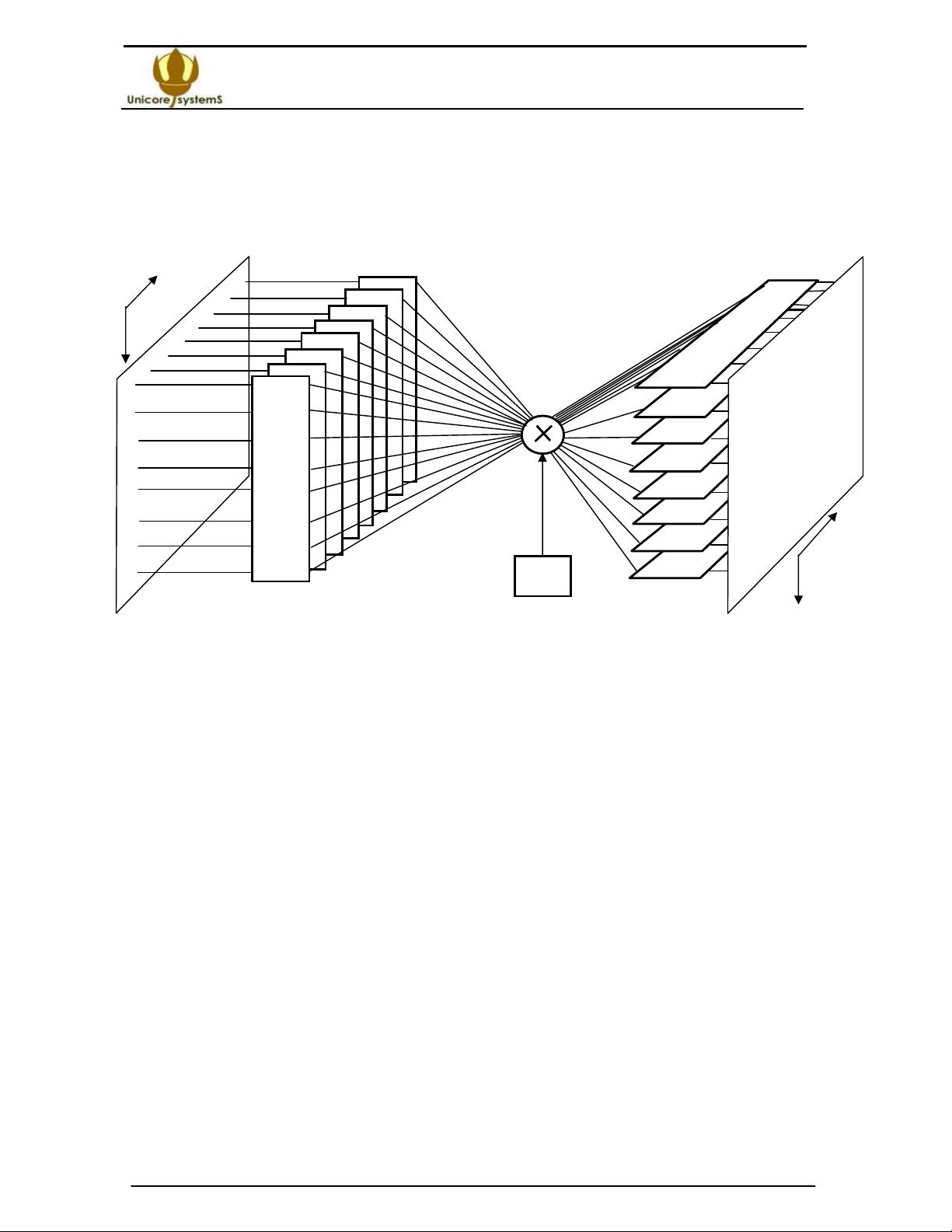
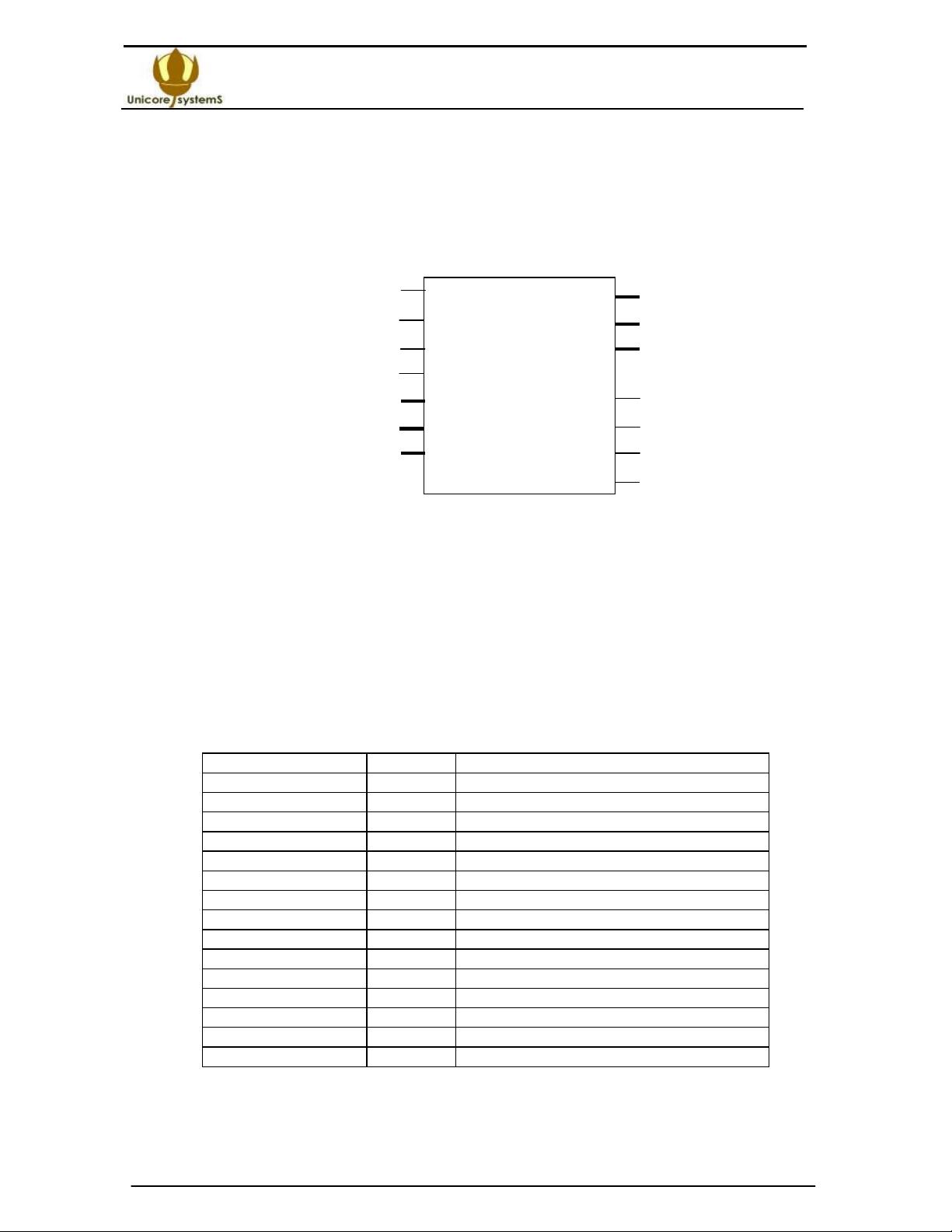
• 256 -point radix-8 FFT.
• Forward and inverse FFT.
• Pipelined mode operation, each result is outputted in one clock cycle, the latent delay from
input to output is equal to 580 clock cycles (839 clock cycles when the direct output data
order), simultaneous loading/downloading supported.
• Input data, output data, and coefficient widths are parametrizable in range 8 to 16 and
more.
• Two and three data buffers are selected.
• FFT for 10 bit data and coefficient width is calculated on Xilinx XC4SX25-12 FPGA at 250
MHz clock cycle, and on Xilinx XC5SX25-12 FPGA at 300 MHz clock cycle, respectively.
• FFT unit for 10 bit data and coefficients, and 2 data buffers occupies 1652 CLB slices, 4
DSP48 blocks, and 2,5 kbit of RAM in Xilinx XC4SX25 FPGA, and 670 CLB slices 4
DSP48E blocks, and 2,5 kbit of RAM in Xilinx XC5SX25 FPGA, data buffers are
implemented on the distributed RAM.
Unicore Systems Ltd
60-A Saksaganskogo St
Office 1
Kiev 01033
Ukraine
Phone: +38-044-289-87-44
Fax: : +38-044-289-87-44
E-mail: o.uzenkov@unicore.co.ua
URL: www.unicore.co.ua
