Factor graphs, belief propagation and variational__inference.pdf

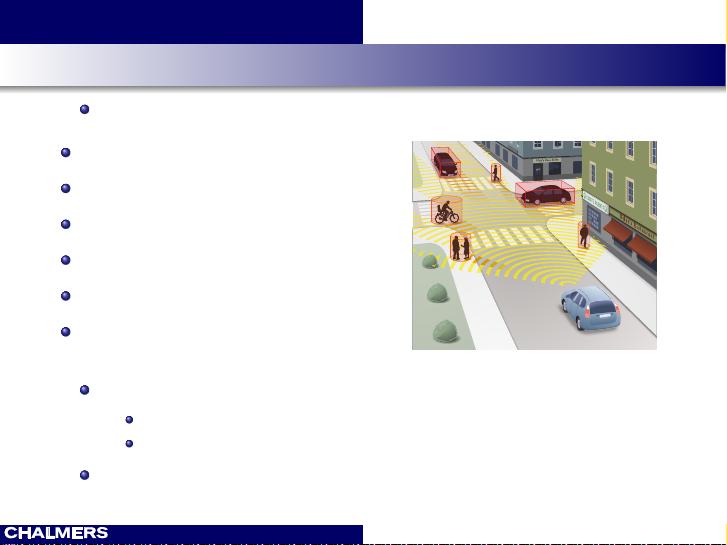
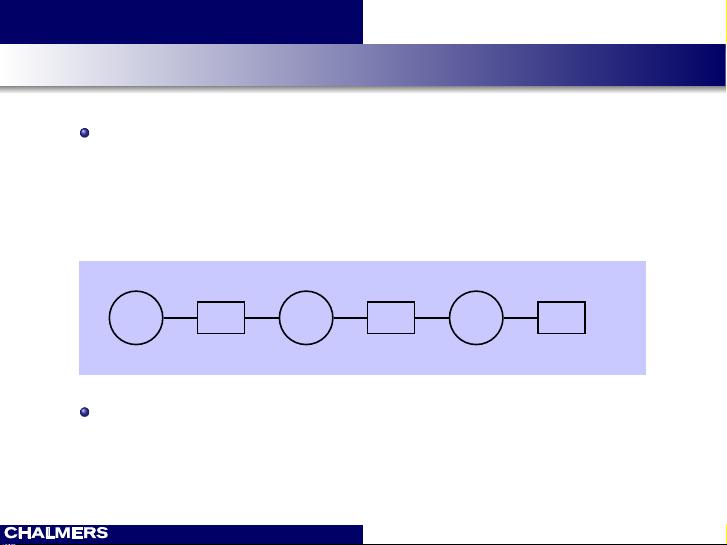
因子图（Factor Graphs）、信念传播（Belief Propagation）和变分推断（Variational Inference）是概率图模型（Probabilistic Graphical Models, PGMs）中三种重要的概念，广泛应用于诸如自动驾驶、协作定位、语音处理、通信系统和图像分割等领域。这些模型的主要目的是揭示问题结构中的条件独立性，并利用这种结构设计可解的推理算法。 因子图（Factor Graphs）是一种双部分图，用于表示联合概率分布中各个因素之间的关系。它们将变量节点（Variable Nodes）与因子节点（Factor Nodes）连接起来，变量节点代表随机变量，因子节点则封装了关于这些变量的局部概率信息。通过因子图，我们可以直观地看到变量间的依赖关系，将一个复杂的多变量函数分解为简单的局部函数，这对于理解和设计高效的算法至关重要。 在因子图上，两个重要的问题通常被关注：一是如何有效地执行算法，特别是在树状结构的因子图上；二是如何处理含有环的因子图。对于树形因子图，我们可以应用消息传递算法，如求和乘积算法（Sum-Product Algorithm，也称贝叶斯网络算法或信念传播），它能有效地进行概率推理，计算变量的后验概率。然而，当因子图包含环时，简单的消息传递就不再适用，需要更复杂的方法来处理。 信念传播是一种在因子图上进行近似推理的方法，它通过在变量节点和因子节点之间传递消息来估算变量的信念分布。尽管这种方法对于树形图可以得到精确解，但在有环图中只能提供近似解，但其计算效率高，常用于实际问题的求解。 变分推断是一种用来近似难以直接计算的后验概率分布的方法。在贝叶斯框架下，我们试图找到一个易于处理的概率分布，使得它与后验分布之间的差异最小，这个差异通常用Kullback-Leibler散度衡量。通过优化这个目标函数，我们可以得到一个对后验分布的近似表示，这在处理大型或者复杂的概率模型时非常有用。 学习因子图、信念传播和变分推断的知识后，你应该能够根据函数的因子分解构建因子图，理解利用问题结构的重要性，了解在无环因子图上求和乘积算法的工作原理，并掌握变分贝叶斯的基本思想。这些工具和技术是解决实际问题，特别是那些涉及大量不确定性和复杂关系的问题时的关键。通过深入理解和应用这些概念，你可以更有效地处理各种信息处理和决策任务。