
1
Multipath and Doppler Effects and Models
There are two parts in this lecture.
• In Part I, we will first introduce the mutipath propagation effects and
Doppler frequency shift/spread effects.
• In Part II, we will briefly introduce multipath and Doppler channel models.

2
Background: Overviews on Wireless Channel Modeling
We need to ask the following three important questions while designing a wireless
communication link:
1. Fading & Power Loss:
Is the signal to interference plus noise ratio (SINR) large enough for the receiver
to detect the transmitted signal?
2. Signal Distortion:
Can the signal distortion be ignored, predicted or removed so that we know how
to recover the transmitted information at the receiver?
3. Time Variation:
Can the receiver adapt faster enough to the variations of the above two features
(SINR & signal distortion)?
A complete wireless channel model should provide quantitative measures of SINR,
signal distortion and time variation.
For SINR (referred in question 1), we need only to consider the time invariant
transmission loss at a single frequency (that is the RF carrier frequency). The
frequency and time dependent properties of signal can be addressed in answering
questions 2 and 3.
Signal distortion (referred in question 2) is caused by the frequency dependent
variations of the received signal strength and phase. The primary source of
frequency dependent variations is multipath propagation. Here, we need only to
consider time invariant situations and leave the time varying features to question 3.
Motions of receivers, transmitters or wireless environments generate Doppler
effects. With Doppler effects, signal frequencies shift and spread. These Doppler
effects will cause time variations in the received signal strength and wave shape.
This kind of time varying features is usually random and can be modeled as
stochastic processes.
In order to addressing these three important issues, we divide wireless channel modeling
into three parts:
• Transmission loss
-single frequency (or narrowband signal)
-time invariant environment (or short observation time period)
• Frequency dependent channel impulse response or transfer function
-multiple frequencies (or broadband signal)
-time invariant environment (or short observation time period)
• Time varying channel impulse response or transfer function
-multiple frequencies (or broadband signal)

3
-time varying environment (or long observation time period)
We have discussed transmission loss (including path loss, short term fading and long
term fading) of a single frequency response in time invariant environments in the
previous lecture. Both frequency dependent and time varying features of a channel
impulse response (or transfer function) will be introduced in this lecture.
4
Part I: Multipath and Doppler Effects
After studying this note, students will be able to
1. Understand multipath channel effects in both time and frequency domains
2. Understand Doppler effects in both time and frequency domains
3. Understand multipath and Doppler effects in both time and frequency domains
I. Multipath Channel Effects: Time Invariant Case (No Doppler effects)
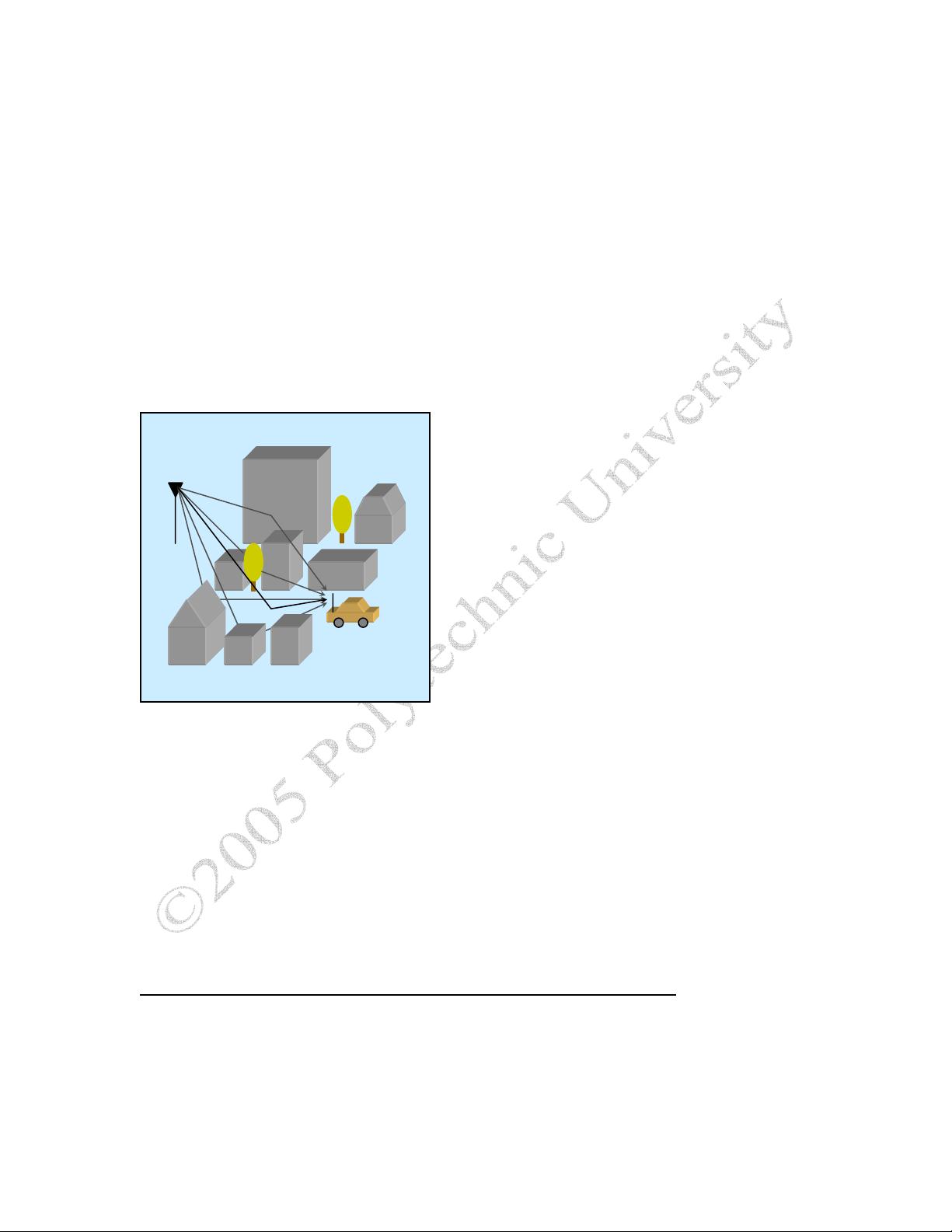
In wireless communication environments, a signal transmitted from the transmitter
reaches the receiver through many different paths as illustrated in Figure 1.
Let s(t) is the transmitted signal. The received signal can then be written as a sum of
multipath arrivals:
123
1
( ) ( ), ....
L
ii L
i
yt ast
τ
τττ τ
=
=−≤≤≤≤
∑
(1)
Here, L is the total number of multipath arrivals, a
i
and
τ
i
are the amplitude and arrival
time of the i
th
ray, respectively.
A. s(t) is a time harmonic (i.e., single frequency or sinusoidal) signal
Consider the transmitted signal ( )
jt
st e
ω
= . Then, the received signal is
()
11
( ) ( ) with ( )
n n
LL
jt j
jt
nn
nn
yt ae H e H ae
ω
τωτ
ω
ωω
−−
==
== =
∑∑
(2)
Fi
g
ure 1: Multi
p
ath
p
ro
p
a
g
ation

5
Here,
()H
ω
is defined as the transfer function of the multipath environment. Note that
the receiver signal y(t) remains as a
time harmonic signal with the same angular
frequency
ω
as the transmitted signal s(t). Thus, no distortion in wave shape has
occurred during the transmission of s(t) through a time invariant multipath environment.
However, the magnitude of the signal has been modified. The new magnitude is
()H
ω
which is a function of angular frequency
ω
.
We use the following matlab code to generate the Figure 2:
========================================================
clear all;
% amplitudes of 7 multipath arrivals
a=[0.6154 0.7919 0.9218 0.7382 0.1763 0.4057 0.9355];
% arrival times of 7 multipath arrivals
t=[0.9169 0.4103 0.8936 0.0579 0.3529 0.8132 0.0099];
i=0; % frequency index
for omega=0:0.05:100; % angular freuencies
multipath_arrival=a.*exp(j*omega*t);
i=i+1;
abs_H(i)=abs(sum(multipath_arrival)); % the i-th transfer function
end
omega=0:0.05:100;
plot(omega, abs_H)
ylabel('amplitude of transfer function')
xlabel('angular freuency')
title('frequency dependent multipath fading')
Here, we use 7 multipath arrivals. The amplitudes and arrival times of these seven
multipath arrivals are randomly chosen. From Figure 2, the magnitude of received signal
fluctuates as angular frequency changes. For some frequencies, the 7 multipath arrivals
interfere destructively and yield small
()H
ω
. For other frequencies, the 7 multipath
arrivals interfere constructively and yield large
()H
ω
. This phenomenon is called
multipath fading. Figure 2 shows that multipath fading is frequency dependent. Other
kinds of fading will be discussed in future lectures.
















