
Adaptive Grids for
Clustering Massive Data
Sets
∗
Harsha Nagesh
†
, Sanjay Goil
‡
, and Alok Choud-
hary
§
Clustering is a key data mining problem. Density and grid based technique is
a popular way to mine clusters in a large multi-dimensional space wherein clusters
are regarded as dense regions than their surroundings. The attribute values and
ranges of these attributes characterize the clusters. Fine grid sizes lead to a huge
amount of computation while coarse grid sizes result in loss in quality of clusters
found. Also, varied grid sizes result in discovering clusters with different cluster
descriptions. The technique of Adaptive grids enables to use grids based on the data
distribution and does not require the user to specify any parameters like the grid
size or the density thresholds. Further, clusters could be embedded in a subspace
of a high dimensional space. We propose a modified bottom-up subspace clustering
algorithm to discover clusters in all possible subspaces. Our method scales linearly
with the data dimensionality and the size of the data set. Experimental results
on a wide variety of synthetic and real data sets demonstrate the effectiveness of
Adaptive grids and the effect of the modified subspace clustering algorithm. Our
algorithm explores at-least an order of magnitude more number of subspaces than
the original algorithm and the use of adaptive grids yields on an average of two
orders of magnitude speedup as compared to the method with user specified grid
size and threshold.
∗
This work was supported in part by NSF Young Investigator Award CCR-9357840, NSF
CCR-9509143 and Department of Energy ASCI/ASAP program
†
Mr.Harsha Nagesh, Bell-labs Research, Murray Hill, NJ, harsha@research.bell-labs.com
‡
Dr. Sanjay Goil, Sun Microsystems Inc., sanjay.goil@eng.sun.com
§
Prof. Alok Choudhary, Department of ECE, Northwestern University, choudhar@ece.nwu.edu
1

2
1 Introduction
The ability to identify interesting patterns in large scale consumer data empowers
business establishments to leverage on the information obtained. Clustering process
is a data mining technique which finds such patterns, previously unknown in large
scale data, embedded in a large multi-dimensional space. Clustering techniques
find application in several fields. Clustering web documents based on web logs has
been studied in [1], customer segmentation based on similarity of buying interests
is explored as collaborative filtering in [2], [3] explores the detection of clusters
in geographic information systems. Clustering algorithms need to address several
issues. Scalability of these algorithms with the data base size is as important as
their scalability with the dimensionality of the data sets. Effective representation
of the detected clusters is as important as cluster detection. Simplicity in reporting
clusters among those found improves the usability of the algorithm. Further, most
clustering algorithms require key input parameters from the user which are hard to
determine and also greatly control the process of cluster detection. Clusters could
also be embedded in a subspace of the total data space. Detection of clusters in all
possible subspaces results in an exponential algorithm as the number of subspaces is
exponential in the data dimension. Most of the earlier works in statistics and data
mining [4, 5] operate and find clusters in the whole data space. Many clustering
algorithms [3, 6, 5] require user input of several parameters like the number of
clusters, average dimensionality of the cluster, etc. which are not only difficult to
determine but are also not practical for real-world data sets.
We use a grid and density based approach for cluster detection in subspaces.
Density based approaches regard clusters as high density regions than their sur-
roundings. In a grid and density approach a multi-dimensional space is divided into
a large number of hyper-rectangular regions and regions which have more points
than a specified threshold are identified as dense. Finally dense hyper-rectangular
regions that are adjacent to each other are merged to find the embedded clusters.
The quality of results and the computation requirements heavily depend on the
number of bins in each dimension. Hence, determination of bin sizes automati-
cally based on the data distribution greatly helps in finding correct clusters of high
quality and reduces the computation substantially.
1.1 Contributions
In this paper we present MAFIA
1
, a scalable subspace clustering algorithm using
adaptive computation of the finite intervals (bins) in each dimension, which are
merged to explore clusters in higher dimensions. Adaptive grid sizes improves the
clustering quality by concentrating on the portions of the data space which have
more points and thus are more likely to be part of a cluster region enabling minimal
length DNF expressions, important for interpreting results by the end-user. MAFIA
does not require any key user inputs and takes in only the strength of the clusters
that needs to be discovered in the given data set. Further, we present a modi-
fied bottom-up algorithm for cluster detection in all possible subspaces previously
1
Merging of Adaptive Finite Intervals

3
unexplored by other subspace clustering algorithms. We describe recent work on
clustering techniques in databases in Section 2. Density and grid based clustering
is presented in Section 3, where we describe subspace clustering as introduced by
[7] and also describe our approach of using adaptive grids. Section 4 presents the
modified subspace clustering algorithm with a theoretical analysis. Finally, Section
5 presents the performance evaluation on a wide variety of synthetic and real data
sets with large number of dimensions, highlighting both scalability of the algorithms
and the quality of the clustering. Section 6 concludes the paper.
2 Related Work
Clustering algorithms have long been studied in statistics [8], machine learning
[9], pattern recognition, image processing [10] and databases. k-means, k-mediods,
CLARANS [11], BIRCH [5], CURE [12] are some of the earlier works. However,
none of these algorithms detect clusters in subspaces. PROCLUS [6], a subspace
clustering algorithm finds representative cluster centers in an appropriate set of
cluster dimensions. It needs the number of clusters, k, and the average cluster
dimensionality, l, as input parameters, both of which are not possible to be known
a-priori for real data sets. Density and grid based approaches regard clusters as
regions of data space in which objects are dense and are separated by regions of low
object density [13]. The grid size determines the computations and the quality of
the clustering. CLIQUE, a density and grid based approach for high dimensional
data sets [7], detects clusters in the highest dimensional subspaces taking the size
of the grid and a global density threshold for clusters as inputs. The computation
complexity and the quality of clustering is heavily dependent on these parameters.
ENCLUS [14], an entropy based subspace clustering algorithm requires a prohibitive
amount of time to just discover interesting subspaces in which clusters are embedded
and requires entropy thresholds as inputs, which is not intuitive for the user.
3 Density and Grid based Clustering
Density based approaches regard clusters as high density regions than their sur-
roundings. A common way of finding high-density regions in the data space is
based on the grid cell densities [13]. A histogram is constructed by partitioning the
data space into a number of non-overlapping regions and then mapping the data
points to each cell in the grid. Equal length intervals are used in [7] to partition
each dimension, which results in uniform volume cells. The number of points inside
the cell with respect to the volume of the cell can be used to determine the density
of the cell. Clusters are unions of connected high density cells. Two k-dimensional
cells are connected if they have a common face in the k-dimensional space or if
they are connected by a common cell. Creating a histogram that counts the points
contained in each unit is infeasible in high dimensional data as the number of hyper-
rectangles is exponential in the dimensionality of the data set. Subspace clustering
further complicates the problem as it results in an explosion of such units. One
needs to create histograms in hyper-rectangles formed in all possible subspaces. A
bottom-up approach of finding dense units and merging them to find dense clusters
in higher dimensional subspaces has been proposed in CLIQUE [7]. Each dimension

4
is divided into a user specified number of intervals, . The algorithm starts by deter-
mining 1-dimensional dense units by making a pass over the data. In [7] candidate
dense cells in any k dimensions are obtained by merging the dense cells in (k − 1)
dimensions which share the first (k − 2) dimensions. A pass over data is made to
find which of the candidate dense cells are actually dense. The algorithm terminates
when no more candidate dense cells are generated. In [7] candidate dense units are
pruned based on a minimum description length technique to find the dense units
only in interesting subspaces. However, as noted in [7] this could result in missing
some dense units in the pruned subspaces. In order to maintain the high quality of
clustering we do not use this pruning technique.
3.1 Adaptive Grids
We propose an adaptive interval size in which bins are determined based on the data
distribution in a particular dimension. The size of the bin and hence number of
bins in each dimension in turn determine the computation and quality of clustering.
Finer grids leads to an explosion in the number of candidate dense units (CDUs),
while coarser grids leads to fewer bins, and regions with noise data might also get
propagated as dense cells. Also, a user defined uniform grid size may fail to detect
many clusters or may yield very poor quality results. A single pass over the data is
done in order to construct a histogram in every dimension. Algorithm 3.1 describes
the steps of the adaptive grid technique. The domain of each dimension is divided
into fine intervals, each of size x. The size of each bin, x, is selected such that each
dimension has a minimum of 1000 fine bins. If the range of the dimension is from
m to n then we set the number of bins in that dimension to be max(1000, (n −
m)) and correspondingly find the value of x. We assume that all attributes have
been normalized to the same base quantity while finding m, n and hence x. The
maximum of the histogram value within a window is taken to reflect the window
value. Adjacent windows whose values differ by less than a threshold percentage, β,
are merged together to form larger windows ensuring that we divide the dimensions
into variable sized bins which capture the data distribution. However, in dimensions
where data is uniformly distributed this results in a single bin and indicates much
less likelihood of finding a cluster. However, we split the domain into a small fixed
number of partitions, set a high threshold as this dimension is less likely to be part
of a cluster and collect statistics for these bins to examine further. This technique
greatly reduces the computation time by limiting the degree of bin contribution
from non-cluster dimensions . Variable sized bins are assigned a variable threshold.
A variable sized bin is likely to be part of a cluster if it has a significantly (which we
call cluster dominance factor α [15]) greater number of points than it would have
had, had the data been uniformly distributed in that dimension. Thus, for a bin of
size a in a dimension of size D
i
we set its threshold to be
αaN
D
i
, where N is the total
number of data points.
Effect of Adaptive Grids on Computation
Figure 1 shows the histogram of data in two dimensions. Figure 1(a) shows the user
defined uniform sized grid used in the approach of [7] resulting in a large number
of CDUs (rectangles in the figure). With the increase in data set size, each pass
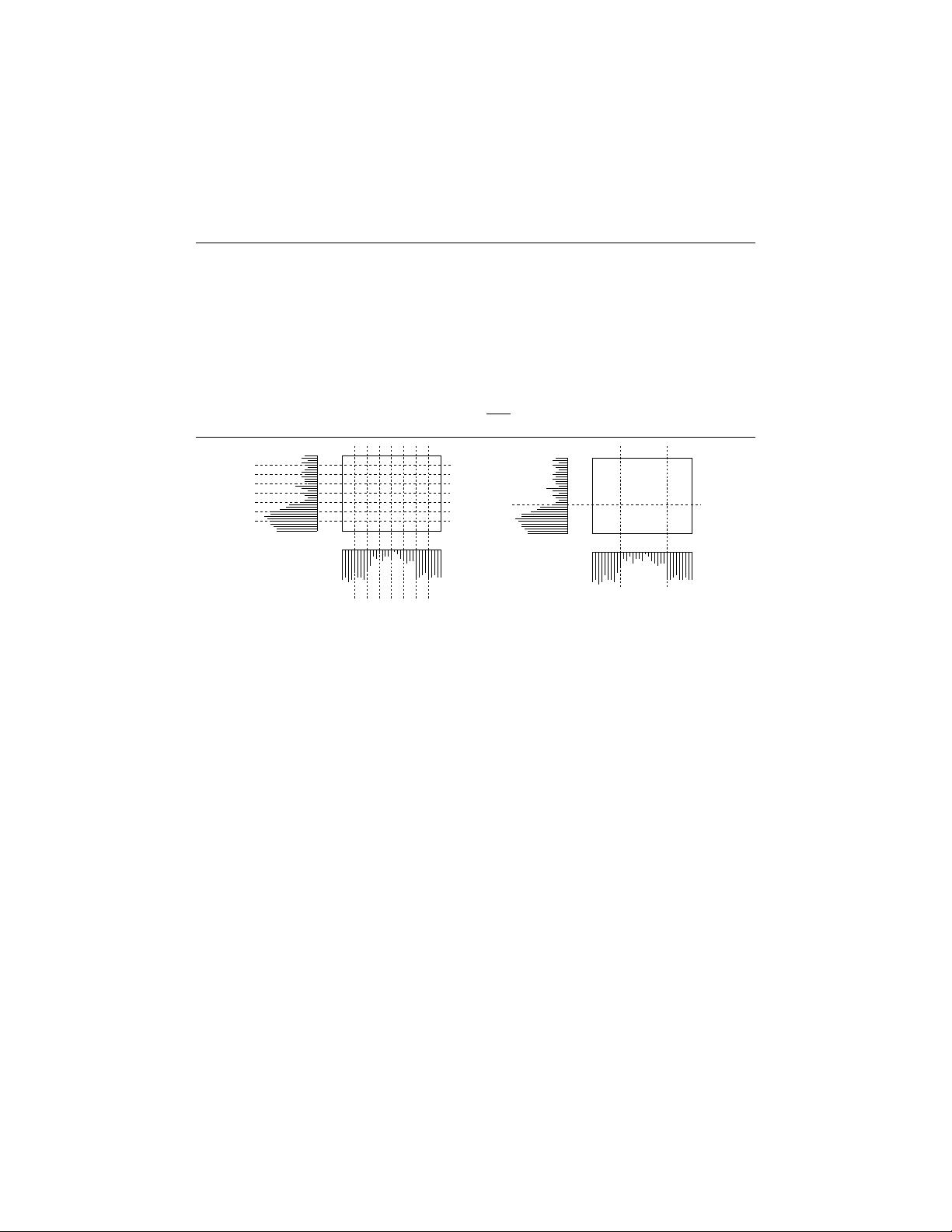
5
Algorithm 3.1 Adaptive Grid Computation
D
i
- Domain of A
i
N - Total number of data points in the data set
a - Size of a generic bin
for each dimension A
i
,i ∈ (1,...d)
Divide D
i
into windows of some small size x
Compute the histogram for each unit of A
i
, and set the value of
the window to the maximum in the window
From left to right merge two adjacent units if they are within a threshold β
/* Single bin implies an equi-distributed dimension */
if(number of bins == 1)
Divide the dimension A
i
into a fixed number of equal partitions.
Compute the threshold of each bin of size a as
αaN
D
i
end
(a) (b)
Figure 1. (a) Uniform grid size (b) Adaptive grid size
over the data in the bottom-up algorithm results in evaluating a large number of
candidate dense units. However, as seen in Figure 1(b) adaptive grids makes use
of the data distribution and computes the minimum number of bins as required in
each dimension resulting in very few CDUs.
Effect of Adaptive Grids on Quality of Clustering
Figure 2 shows a ’plus’ shaped cluster (abcdefghijkl) as discovered by [7] and
our algorithm using adaptive grids. The cluster reported by CLIQUE, pqrs, is
shown in Figure 2(a). Parts of the cluster discovered by [7] are not in the original
defined cluster abcdefghijkl and also parts of the original cluster are thrown away
as outliers. MAFIA uses adaptive grid boundaries and so the cluster definitions are
minimal DNF expressions representing the clusters accurately. MAFIA develops
grid boundaries very close to the boundaries of the cluster and reports abcdefghijkl
shown in Figure 2(b) as the cluster with the DNF expression (l, y) ∧(m, z) ∧ (n, y) ∧
(m, x) ∧ (m, y).
4 MAFIA Implementation
MAFIA consists mainly of the following steps. The algorithm starts by making a
pass over the data in chunks of B records to enables scaling to out-of-core data
sets. A histogram of the data is built in each dimension as elaborated in Algorithm
3.1. The adaptive finite intervals in every dimension is determined and the bin sizes
















