MATLAB eXtended Finite Element Method
(MXFEM)
User's Guide
Matthew Jon Pais
Structural and Multidisciplinary Optimization Group
Mechanical and Aerospace Engineering Department
University of Florida
Gainesville, FL 32611
April 30, 2010
2
Table of Contents
Chapter 1: Introduction ................................................................................... 3
Chapter 2: eXtended Finite Element Method .................................................4
Chapter 3: Level Set Method .......................................................................... 6
Chapter 4: Fracture Mechanics .......................................................................8
Chapter 5: Reanalysis....................................................................................10
Chapter 6: Use of MXFEM...........................................................................12
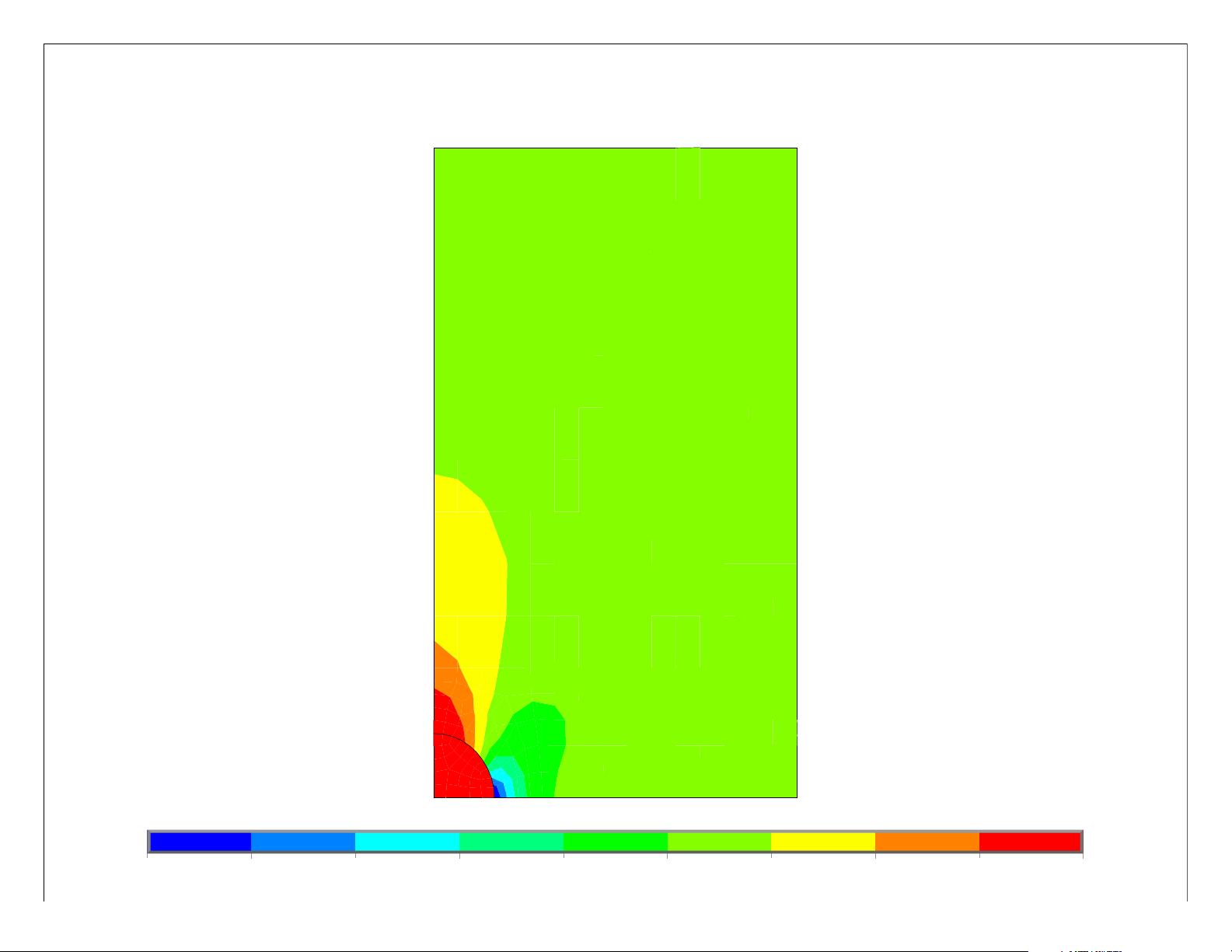
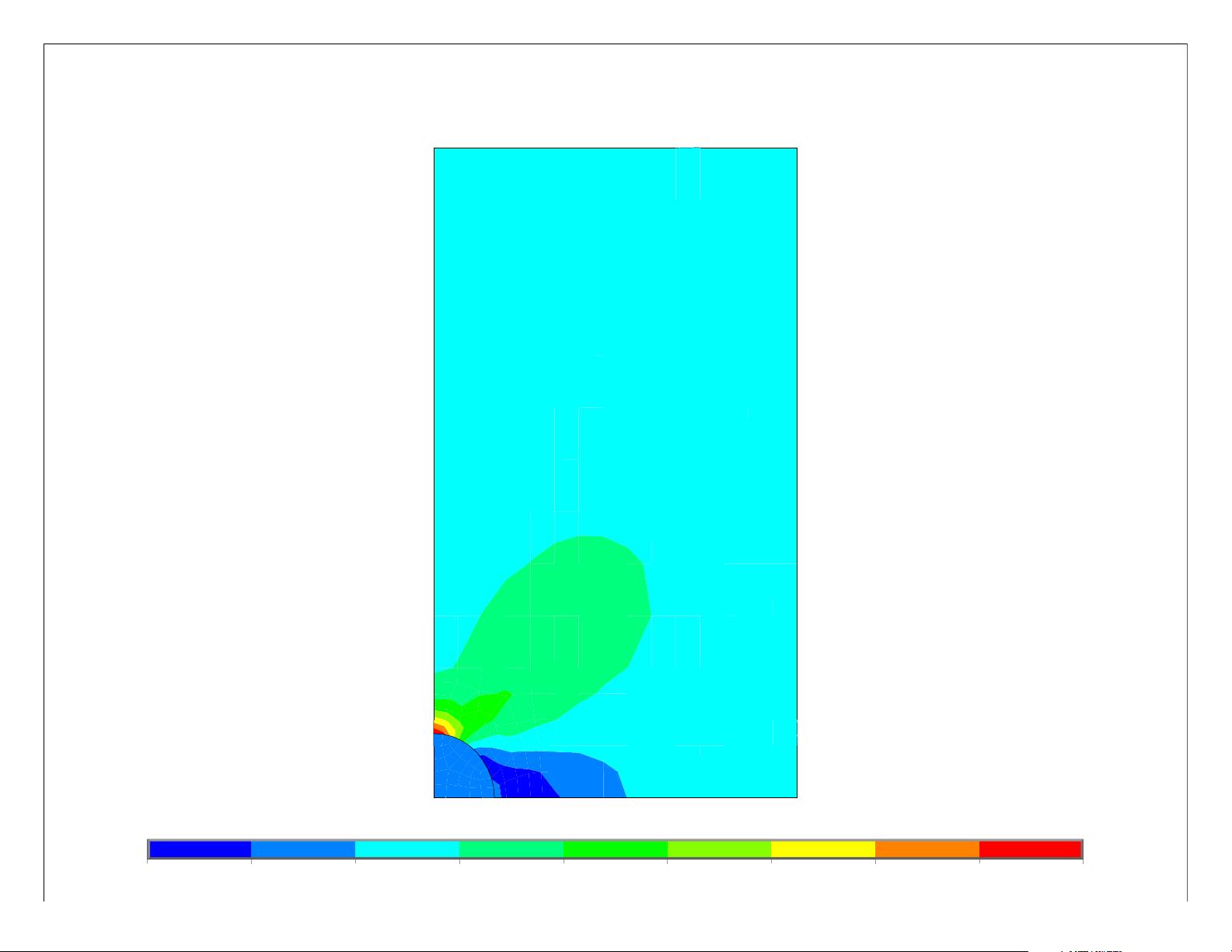
Chapter 7: Examples .....................................................................................17
1. Center Crack in a Finite Plate Under Uniaxial Tension ....................................... 17
2. Edge Crack in a Finite Plate Under Uniaxial Tension.......................................... 17
3. Circular Inclusion in a Finite Plate ....................................................................... 18
4. Circular Void in a Finite Plate .............................................................................. 18
5. Paris Crack Growth Law....................................................................................... 18
6. Crack Growth in Presence of a Hard/Soft Inclusion............................................. 18
7. Crack Initiation Angle for Crack Initiating from a Hole in a Plate ...................... 19
Appendix: Auxiliary Stress Fields ................................................................20
References .....................................................................................................21

3
Chapter 1: Introduction
Modeling crack growth in a traditional finite element framework is a challenging engineering task.
Originally the finite element framework was modified to accommodate the discontinuities that are caused
by phenomena such as cracks, inclusions and voids. The finite element framework is not well suited for
modeling crack growth because the domain of interest is defined by the mesh. At each increment of crack
growth, at least the domain surrounding the crack tip must be remeshed such that the updated crack
geometry is accurately represented.
Here, a simple two-dimensional plane stress and plane strain XFEM implementation within
MATLAB is presented. The extended finite element method (XFEM) along with the level set method can
be used to alleviate many of the inconveniences of using the finite element method (FEM) to model the
evolution of a crack. Special enrichment functions are added to the traditional finite element framework
through the partition of unity framework. For modeling the strong discontinuity of a cracked body two
enrichment functions are used. The Heaviside step function represents the discontinuity away from the
crack tip, and the linear elastic asymptotic crack tip displacement fields are used to account for
discontinuity at the crack tip. The crack is represented independent of the mesh by the enrichment functions
which allows for the crack geometry to be updated without a need to create/update a new mesh on the
domain. In addition, enrichment functions for a bimaterial crack are presented. For the case of a material
interface, an enrichment function is used which combines distance from the weak discontinuity and the
absolute value function. Finally, for a void, a step function is used such that the global displacement
approximation equals zero within the void.
Crack growth was modeled by combining the maximum circumferential stress criterion for predicting
the direction of crack growth. Either a constant crack growth increment or the Paris law is used to
incrementally grow a crack. The stress intensity factors needed for these models were calculated using the
domain form of the J-integral interaction integrals.

4
Chapter 2: eXtended Finite Element Method
The extended finite element method
1,2
(XFEM) allows discontinuities to be represented independent
of the finite element mesh by exploiting the partition of unity finite element method
3
(PUFEM). Arbitrarily
oriented discontinuities can be modeled independent of the finite element mesh by enriching all elements
cut by a discontinuity using enrichment functions satisfying the discontinuous behavior and additional
nodal degrees of freedom. In general the approximation of the displacement field in XFEM takes the
following form:
h
( ) N ( ) ( )
d
I I I
I I
x x xυ
∈Ω ∈Ω
= +
∑ ∑
u u a
(2.1)
where
Ω
is the entire domain and
d
Ω
is the domain containing discontinuities. In Eq. (2.1),
N ( )
I
x
are the
traditional finite element shape function,
( )
x
υ
is the discontinuous enrichment function, and
I
u
,
I
a
are
the traditional and enriched degrees of freedom (DOF). Note that where
d
Ω Ω = ∅
∩
the enrichment
function
( )
x
υ
vanishes. As the discontinuities are not defined by the finite element mesh the level set
method is used to track the discontinuities. The approximation in Eq. (2.1) does not satisfy interpolation
property; i.e.,
( )
h
I I
x
≠
u u
due to enriched degrees of freedom. A common practice to satisfy the
interpolation property in implementations of XFEM is to 'shift' the enrichment function
4
such that
( ) ( ) ( )
I I
x x x
υ υ
ϒ = −
. (2.2)
where
( )
I
x
ϒ
is the shifted enrichment function for the i
th
node and
( )
I
x
υ
is the value of
( )
x
υ
at the i
th
node. Thus, the interpolation property is recovered as the shifted enrichment function
( )
I
x
ϒ
vanishes at
the node. Here lower case variables are used to represent the unshifted enrichment functions.
Crack Enrichment
For the modeling of a crack in a homogeneous material, two different enrichment schemes are
employed. For an element completely cut by a crack the Heaviside
2
enrichment function is used such that
Above Crack
Below Crack
1
h( )
1
x
+
=
−
. (2.3)
Thus a discontinuity is explicitly added to an element cut by a crack.
For the case of an element containing the crack tip the functions originally introduced by Fleming
5
for
the representing crack tip displacement fields in the element-free Galerkin (EFG) method and repeated by
Belytschko
1
are repeated. The near tip displacement field takes the form of the following four functions
1 4
( ), sin , cos , sin cos , sin cos
2 2 2 2
x r r r r
α α
θ θ θ θ
φ θ θ
= −
=
(2.4)
where
r
and
θ
are the polar coordinates in the local crack-tip coordinate system. Note that the crack tip
enrichment functions in Eq. (2.4) introduces a discontinuity across the crack in the element containing the
tip, while the Heaviside function in Eq. (2.3) does in the elements cut by the crack. When a node would be
enriched by both Eqs. (2.3) and (2.4), only Eq. (2.4) is used.
Bimaterial Crack Enrichment
For the case of a bimaterial crack, the enrichment functions introduced by Sukumar
6
are used. Due to
the oscillatory nature of the singularity a more complex near tip displacement field is required which takes
the form of

5
( ) ( )
{
( ) ( )
( ) ( )
( ) ( )
( ) ( )
- -
1 12
-
- -
( ), cos log e sin , cos log e cos ,
2 2
cos log e sin , cos log e cos ,
2 2
cos log e sin sin , cos log e cos sin ,
2 2
sin log e sin , sin log e cos ,
2 2
sin log e sin , sin log e
2
x r r r r
r r r r
r r r r
r r r r
r r r r
εθ εθ
α α
εθ εθ
εθ εθ
εθ εθ
εθ εθ
θ θ
φ ε ε
θ θ
ε ε
θ θ
ε θ ε θ
θ θ
ε ε
θ
ε ε
= −
=
( ) ( )
}
cos ,
2
sin log e sin sin , cos log e cos sin
2 2
r r r r
εθ εθ
θ
θ θ
ε θ ε θ
(2.5)
where
r
and
θ
are polar coordinates in the local crack tip coordinate system and
ε
is a constant which is
a bimaterial constant given by
1 1
log
2 1
β
ε
π β
−
=
+
(2.6)
where
β
is the second Dundurs
7
parameter given by
(
)
(
)
( ) ( )
1 2 2 1
1 2 2 1
1 2 1 2
1 1
v v
v v
µ µ
β
µ µ
− − −
=
− + −
(2.7)
where
µ
is the shear modulus and
v
is Poisson's ratio. Please refer to the paper by Sukumar
6
for the
derivatives of these enrichment functions with respect to the global coordinate system.
Inclusion Enrichment
Sukumar
8
was the first to try and represent a material interface using an enrichment in XFEM. This
enrichment took the form
( ) ( )
I I
I
x N x
ψ ζ
=
∑
(2.8)
where
I
ζ
are the nodal level set values for the material interface level set function. This solution however,
lead to issues with blending between the enriched and unenriched elements. To improve the convergence
rate a minimization problem was formulated which improved the convergence.
Moës
9
then addressed the problem using a modified absolute value enrichment where
( ) ( ) ( )
I I I I
I I
x N x N x
ψ ζ ζ
= −
∑ ∑
. (2.9)
This enrichment was shown to have optimal convergence. In addition, note that the enrichment function
goes to zero at all nodes such that it does not need to be shifted like many other enrichment functions.
Void Enrichment
Voids
8,10
have been modeled independent of the finite element mesh using a different enrichment
strategy which takes the form of
( ) V( ) N ( )
h
I I
I
x x x
∈Ω
=
∑
u u
(2.10)
where
V( )
x
is the void enrichment taking a value of 0 inside the void and 1 outside the void. In two-
dimensions, integration is performed only in the portion of an element containing material and nodes with
support completely within in void are fixed.



















