Semi-SupervisedSparseRepresentationBased资源-CSDN文库

需积分: 9 44 浏览量 2018-01-28 15:43:48 上传评论收藏 3.92MB PDF 举报

资源推荐

资源详情

资源评论

IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 26, NO. 5, MAY 2017 2545

Semi-Supervised Sparse Representation Based

Classiﬁcation for Face Recognition With

Insufﬁcient Labeled Samples

Yuan Gao, Jiayi Ma, and Alan L. Yuille, Fellow, IEEE

Abstract—This paper addresses the problem of face recogni-

tion when there is only few, or even only a single, labeled examples

of the face that we wish to recognize. Moreover, these examples

are typically corrupted by nuisance variables, both linear (i.e.,

additive nuisance variables, such as bad lighting and wearing

of glasses) and non-linear (i.e., non-additive pixel-wise nuisance

variables, such as expression changes). The small number of

labeled examples means that it is hard to remove these nuisance

variables between the training and testing faces to obtain good

recognition performance. To address the problem, we propose a

method called semi-supervised sparse representation-based clas-

siﬁcation. This is based on recent work on sparsity, where faces

are represented in terms of two dictionaries: a gallery dictionary

consisting of one or more examples of each person, and a variation

dictionary representing linear nuisance variables (e.g., different

lighting conditions and different glasses). The main idea is that:

1) we use the variation dictionary to characterize the linear

nuisance variables via the sparsity framework and 2) prototype

face images are estimated as a gallery dictionary via a Gaussian

mixture model, with mixed labeled and unlabeled samples in

a semi-supervised manner, to deal with the non-linear nuisance

variations between labeled and unlabeled samples. We have done

experiments with insufﬁcient labeled samples, even when there is

only a single labeled sample per person. Our results on the AR,

Multi-PIE, CAS-PEAL, and LFW databases demonstrate that

the proposed method is able to deliver signiﬁcantly improved

performance over existing methods.

Index Terms— Gallery dictionary learning, semi-supervised

learning, face recognition, sparse representation based classiﬁ-

cation, single labeled sample per person.

I. INTRODUCTION

ACE Recognition is one of the most fundamental prob-

lems in computer vision and pattern recognition. In the

Manuscript received September 12, 2016; revised January 3, 2017; accepted

February 13, 2017. Date of publication February 28, 2017; date of current

version April 1, 2017. This work was supported in part by the National

Natural Science Foundation of China under Grant 61503288, in part by

the China Postdoctoral Science Foundation under Grant 2016T90725, and

in part by the NSF Award CCF under Grant 1317376. The associate editor

coordinating the review of this manuscript and approving it for publication was

Prof. Amit K. Roy Chowdhury. (Corresponding author: Jiayi Ma.)

Y. Gao is with the Electronic Information School, Wuhan University, Wuhan

430072, China, and also with the Tencent AI Laboratory, Shenzhen 518057,

China (e-mail: ethan.y.gao@gmail.com).

J. Ma is with the Electronic Information School, Wuhan University, Wuhan

430072, China (e-mail: jyma2010@gmail.com).

A. L. Yuille is with the Department of Statistics, University of California

at Los Angeles, Los Angeles, CA 90095 USA, and also with the Department

of Cognitive Science, Department of Computer Science, Johns Hopkins

University, Baltimore, MD 21218 USA (e-mail: yuille@stat.ucla.edu).

Color versions of one or more of the ﬁgures in this paper are available

online at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/TIP.2017.2675341

past decades, it has been extensively studied because of its

wide range of applications, such as automatic access con-

trol system, e-passport, criminal recognition, to name just

a few. Recently, the Sparse Representation based Classiﬁ-

cation (SRC) method, introduced by Wright et al. [1], has

received a lot of attention for face recognition [2]–[5]. In SRC,

a sparse coefﬁcient vector was introduced in order to represent

the test image by a small number of training images. Then

the SRC model was formulated by jointly minimizing the

reconstruction error and the 

-norm on the sparse coefﬁcient

vector [1]. The main advantages of SRC have been pointed

out in [1] and [6]: i) it is simple to use without carefully

crafted feature extraction, and ii) it is robust to occlusion and

corruption.

One of the most challenging problems for practical face

recognition application is the shortage of labeled samples [7].

This is due to the high cost of labeling training samples by

human effort, and because labeling multiple face instances

may be impossible in some cases. For example, for terrorist

recognition, there may be only one sample of the terrorist,

e.g. his/her ID photo. As a result, nuisance variables (or

so called intra-class variance) can exist between the testing

images and the limited amount of training images, e.g. the

ID photo of the terrorist (the training image) is a standard

front-on face with neutral lighting, but the testing images

captured from the crime scene can often include bad lighting

conditions and/or various occlusions (e.g. the terrorist may

wear a hat or sunglasses). In addition, the training and testing

images may also vary in expressions (e.g. neutral and smile) or

resolution. The SRC methods may fail in these cases because

of the insufﬁciency of the labeled samples to model nuisance

variables [8]–[12].

In order to address the insufﬁcient labeled samples problem,

Extended SRC (ESRC) [13] assumed that a testing image

equals a prototype image plus some (linear) variations. For

example, a image with sunglasses is assumed to equal to

the image without sunglasses plus the sunglasses. Therefore,

ESRC introduced two dictionaries: (i) a gallery dictionary con-

taining the prototype of each person (these are the persons to

be recognized), and (ii) a variation dictionary which contains

nuisance variations that can be shared by different persons

(e.g. different persons may wear the same sunglasses). Recent

improvements on ESRC can give good results for this problem

even when the subject only has a single labeled sample

(namely the Single Labeled Sample Per Person problem,

i.e. SLSPP) [14]–[17].

See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

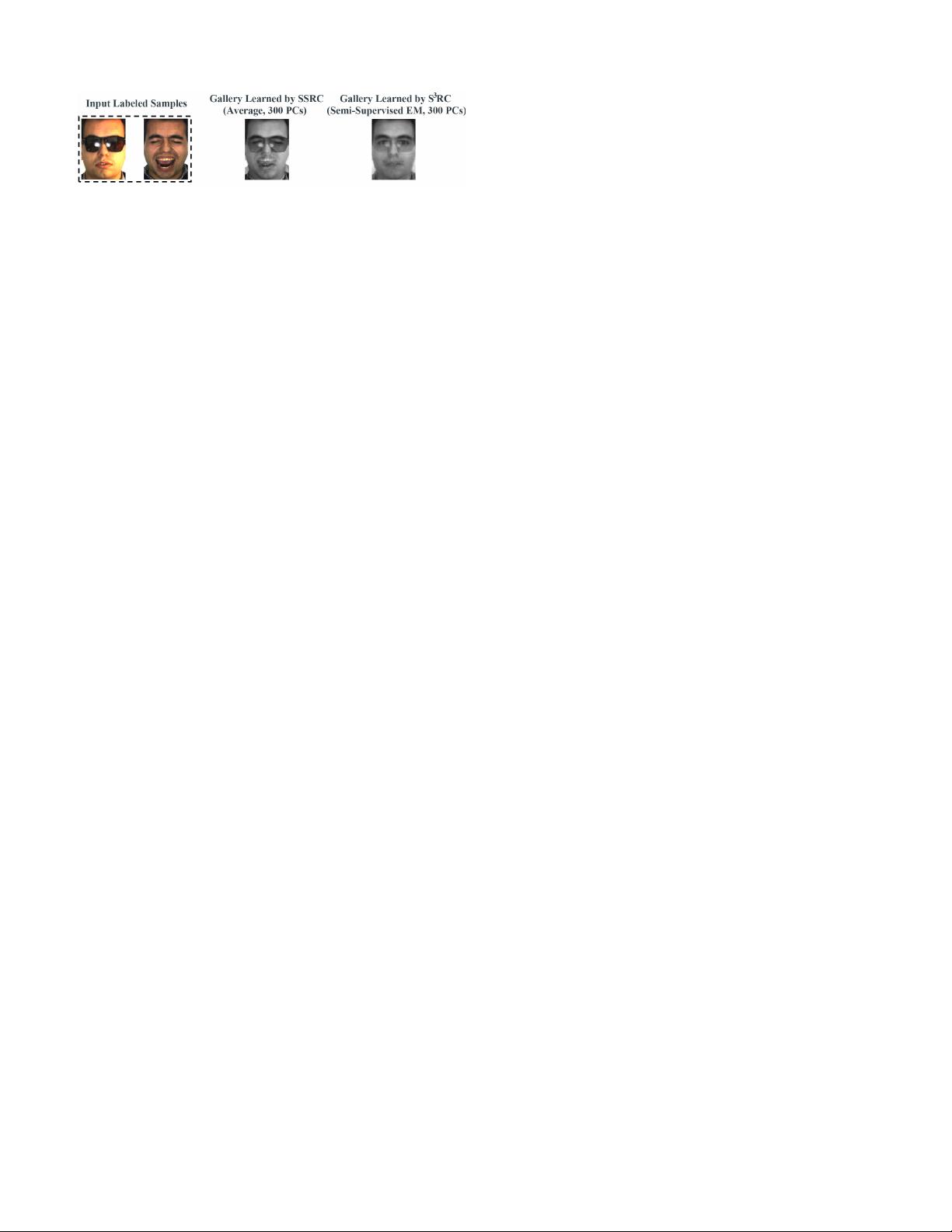
2546 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 26, NO. 5, MAY 2017

Fig. 1. Comparisons of the gallery dictionaries estimated by SSRC

(i.e. the mean of the labeled data) and our method (i.e. one Gaussian centroid

of GMM by semi-supervised EM initialized by the labeled data mean) using

ﬁrst 300 Principal Components (PCs, dimensional reduction by PCA). This

illustrates that our method can estimate a better gallery dictionary with very

few labeled images which contains both linear (i.e. occlusion) and non-linear

(i.e. smiling) variations. The gallery from our method is learned by 5 semi-

supervised EM iterations.

However, various non-linear nuisance variables also exist

in human face images, which makes prototype images hard

to obtain. In other words, the nuisance variables often occur

pixel-wise, which are not additive and cannot shared by dif-

ferent persons. For example, we cannot simply add a speciﬁc

variation to a neutral image (i.e. the labeled training image)

to get its smile images (i.e. the testing images). Therefore,

the limited number of training images may not yield a good

prototype to represent the testing images, especially when

non-linear variations exist between them. Attempts were to

learn the gallery dictionary (i.e. better prototype images) in

Superposed SRC (SSRC) [18]. However, it requires multiple

labeled samples per subject, and still used simple linear

operations (i.e. averaging the labeled faces w.r.t each subject)

to get the gallery dictionary.

In this paper, we propose a probabilistic framework called

Semi-Supervised Sparse Representation based Classiﬁcation

RC) to deal with the insufﬁcient labeled sample problem

in face recognition, even when there is only one labeled

sample per person. Both linear and non-linear variations

between the training labeled and the testing samples are

considered. We deal with the linear variations by a variation

dictionary. After eliminated the linear variation (by simple

subtraction), the non-linear variation is addressed by pursuing

a better gallery dictionary (i.e. better prototype images) via

a Gaussian Mixture Model (GMM). Speciﬁcally, in our pro-

posed S

RC, the testing samples (without label information)

are also exploited to learn a better model (i.e. better prototype

images) in a semi-supervised manner to eliminate the non-

linear variation between the labeled and unlabeled samples.

This is because the labeled samples are insufﬁcient, and

exploiting the unlabeled samples ensures that the learned

gallery (i.e. the better prototype) can well represent the testing

samples and give better results. An illustrative example which

compares the prototype image learned from our method and

the existing SSRC is given in Fig. 1. Clearly from Fig. 1,

we can see that, with insufﬁcient labeled samples, a better

gallery dictionary is learned by S

RC that can well address the

non-linear variations. Also Figs. 8 and 12 in the later sections

show that the learned gallery dictionary of our method can well

represent the testing images for better recognition results.

In brief, since the linear variations can be shared by different

persons (e.g. different persons can wear the same sunglasses),

therefore, we model the linear variations by a variation dictio-

nary, where the variation dictionary is constructed by a large

pre-labeled database which is independent of the training or

testing. Then, we rectify the data to eliminate linear variations

using the variation dictionary. After that, a GMM is applied to

the rectiﬁed data, in order to learn a better gallery dictionary

that can well represent the testing data which contains non-

linear variation from the labeled training. Speciﬁcally, all

the images from the same subject are treated as a Gaussian

with its Gaussian mean as a better gallery. Then, the GMM

is optimized to get the mean of each Gaussian using the

semi-supervised Expectation-Maximization (EM) algorithm,

initialized from the labeled data, and treating the unknown

class assignment of the unlabeled data as the latent variable.

Finally, the learned Gaussian means are used as the gallery

dictionary for sparse representation based classiﬁcation. The

major contributions of our model are:

• Our model can deal with both linear and non-linear

variations between the labeled training and unlabeled

testing samples.

• A novel gallery dictionary learning method is proposed

which can exploit the unlabeled data to deal with the

non-linear variations.

• Existing variation dictionary learning methods are com-

plementary to our method, i.e. our method can be applied

to other variation dictionary learning method to achieve

improved performance.

The rest of the paper is organized as follows. We ﬁrst sum-

marize the notation and terminology in the next subsection.

Section II describes background material and related work.

SSRC and ESRC are described in Section III. In Section IV,

starting with the insufﬁcient training samples problem, we

introduce the proposed S

RC model, discuss the EM opti-

mization, and then we extend S

RC to the SLSPP problem.

Extensive simulations have been conducted in Section V,

where we show that by using our method as a classiﬁer,

further improved performance can be achieved using Deep

Convolution Neural Network (DCNN) features. Section VI

discusses the experimental results, and is followed by con-

cluding remarks in Section VII.

A. Summary of Notation and Terminology

In this paper, capital bold and lowercase bold symbols are

used to represent matrices and vectors, respectively. 1

∈ R

d×1

denotes the unit column vector, and I is the identity matrix.

|| · ||

, || · ||

denote the 

, 

, and Frobenius norms,

respectively. ˆa is the estimation of parameter a.

In the following, we demonstrate the promising performance

of our method on two problems with strictly limited labeled

data: i) the insufﬁcient uncontrolled gallery samples problem

without generic training data, and ii) the SLSPP problem

with generic training data. Here, uncontrolled samples are

images containing nuisance variables such as different illu-

mination, expression, occlusion, etc. We call these nuisance

variables as intra-class variance in the rest of the paper. The

generic training dataset is an independent dataset w.r.t the

training/testing dataset. It contains multiple samples per person

to represent the intra-class variance. In the following, we use

the insufﬁcient training samples problem to refer to the former

problem, and the SLSPP problem is short for the latter one.

GAO et al.:S

RC FOR FACE RECOGNITION WITH INSUFFICIENT LABELED SAMPLES 2547

We do not distinguish the terms training/gallery/labeled sam-

ples, testing/unlabeled samples in the following. But note that

the gallery samples and gallery dictionary are not identical.

The latter means the learned dictionary for recognition.

The promising performance of our method is obtained

by estimating the prototype of each person as the gallery

dictionary, and the prototype is estimated using both labeled

and unlabeled data. Here, the prototype means a learned image

that represents the discriminative features of all the images

from a speciﬁc subject. There is only one prototype for each

subject. Typically, the prototype can be the neutral image of a

speciﬁc subject without occlusion and obtained under uniform

illumination. Our method learn the prototype by estimating

the true centroid for both labeled and unlabeled data of each

person, thus we do not distinguish the prototype and true

centroid in the following.

II. R

ELATED WORK

The proposed method is a Sparse Representation based

Classiﬁcation (SRC) method. Many research works have been

inspired by the original SRC method [1]. In order to learn a

more discriminative dictionary, instead of using the training

data itself, Yang et al. introduced the Fisher discrimination

criterion to constrain the sparse code in the reconstructed

error [19], [20]. Ma et al. learned another discriminative dic-

tionary by imposing low-rank constraints on it [21]. Following

these approaches, a model unifying [19] and [21] was proposed

by Li et al. [22], [23]. Alternatively, Zhang et al. proposed

a model to indirectly learn the discriminative dictionary

by constraining the coefﬁcient matrix to be low-rank [24].

Chi and Porikli incorporated SRC and Nearest Subspace

Classiﬁer (NSC) into a uniﬁed framework, and balanced them

by a regularization parameter [25]. However, this category of

methods need sufﬁcient samples of each subject to construct

an over-complete dictionary for modeling the variations of the

uncontrolled samples [8]–[10], and hence is not suitable for the

insufﬁcient training samples problem and the SLSPP problem.

Recently, ESRC was proposed to address the limitations of

SRC when the number of samples per class is insufﬁcient

to obtain an over-complete dictionary, where a variation dic-

tionary is introduced to represent the linear variation [13].

Motivated by ESRC, Yang et al. proposed the Sparse Variation

Dictionary Learning (SVDL) model to learn the variation

dictionary V, more precisely [14]. In addition to model-

ing the variation dictionary by a linear illumination model,

Zhuang et al. [15], [16] also integrated auto-alignment into

their method. Gao et al. [26] extended the ESRC model by

dividing the image samples into several patches for recogni-

tion. Wei and Wang proposed robust auxiliary dictionary learn-

ing to learn the intra-class variation [17]. The aforementioned

methods did not learn a better gallery dictionary to deal with

non-linear variation, therefore good prototype images (i.e. the

gallery dictionary) were hard to obtain. To address this issue,

Deng et al. proposed SSRC to learn the prototype images as

the gallery dictionary [18]. But this uses only simple linear

operations to estimate the gallery dictionary, which requires

sufﬁcient labeled gallery samples and it is still difﬁcult to

model the non-linear variation.

There are semi-supervised learning (SSL) methods

which use sparse/low-rank techniques. For example,

Yan and Wang [27] used sparse representation to construct

the weight of the pairwise relationship graph for SSL.

He et al. [28] proposed a nonnegative sparse algorithm

to derive the graph weights for graph-based SSL. Besides

the sparsity property, Zhuang et al. [29], [30] also imposed

low-rank constraints to estimate the weight matrix of the

pairwise relationship graph for SSL. The main difference

between them and our proposed method S

RC is that the

previous works used sparse/low-rank technologies to learn

the weight matrix for graph-based SSL, which are essentially

SSL methods. By contrast our method aims at learning a

precise gallery dictionary in the ESRC framework, and the

gallery dictionary learning was assisted by probability-based

SSL (GMM), which is essentially a SRC method. Also

note that as a general tool, GMM has been used for face

recognition for a long time since Wang and Tang [31].

However, to the best of our knowledge, GMM has not been

previously used for gallery dictionary learning in SRC based

face recognitions.

III. S

EMI-SUPERVISED SPARSE REPRESENTATION BASED

CLASSIFICATION WITH EM ALGORITHM

In this section, we present our proposed S

RC method

in detail. Firstly, we introduce the general SRC formulation

with the gallery plus variation framework, in which the linear

variation is directly modeled by the variation dictionary. Then,

we prove that, after eliminating linear variations of each

sample (which we call rectiﬁcation), the rectiﬁed data (both

labeled and unlabeled) from one person can be modeled

as a Gaussian to learn the non-linear variations. Following

this, the whole rectiﬁed dataset including both labeled and

unlabeled samples are formulated by a GMM. Next, initialized

by the labeled data, the semi-supervised EM algorithm is

used to learn the mean of each Gaussian as the prototype

images. Then, the learned gallery dictionary is used for face

recognition by the gallery plus variation framework. After that,

we describe the way to apply S

RC to the SLSPP problem.

Finally, the overall algorithm is summarized.

We use the gallery plus variation framework to address

both linear and non-linear variations. Speciﬁcally, the linear

variation (such as illumination changes, different occlusions)

is modeled by the variation dictionary. After eliminating

the linear variation, we address the non-linear variation

(e.g. expression changes) between the labeled and unla-

beled samples by estimating the centroid (prototype) of each

Gaussian of the GMM. Note that GMM learn the class centroid

(prototype) by semi-supervised clustering, i.e. we only use

the ground truth label as supervised information, the class

assignment of the unlabeled data is treated as the latent

variable in EM and updated iteratively during learning the

class centroid (prototype).

A. The Gallery Plus Variation Framework

The SRC with gallery plus variation framework has been

applied to the face recognition problem as follows. The

剩余15页未读，继续阅读

评论收藏

内容反馈

weixin_41623626

粉丝: 0
资源: 2

Semi-Supervised Sparse Representation Based

最新资源