2014斯坦福大学机器学习mkv视频 Lecture2.pptx

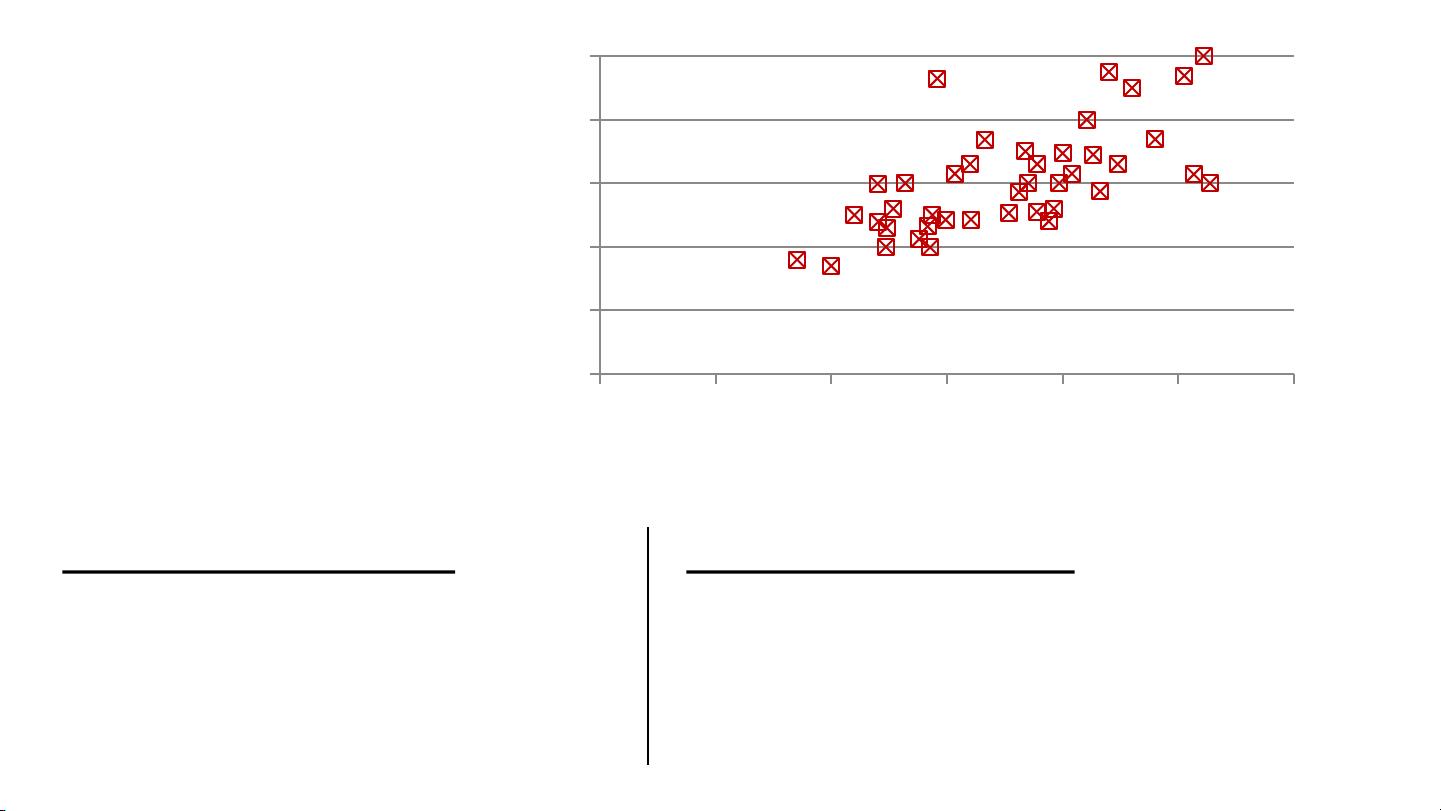
《机器学习基础：线性回归》 在机器学习领域，线性回归是一种基本且重要的算法，主要用于预测连续数值型的输出结果。本讲主要讲解单变量线性回归，由斯坦福大学的Andrew Ng教授授课，内容涉及模型表示、成本函数以及参数选择。 一、线性回归模型表示 线性回归模型通常用来建立输入特征（x）与输出目标（y）之间的关系。在单变量线性回归中，我们假设存在一个线性的函数h，将输入变量x映射到输出变量y。以房价预测为例，假设输入是房屋的面积（x，单位为平方英尺），输出是房价（y，单位为千美元）。模型可以表示为： \[ h(x; \theta) = \theta_0 + \theta_1 x \] 其中，\(\theta_0\) 和 \(\theta_1\) 是模型的参数，分别称为截距和斜率。在训练数据集上，我们有多个房屋的价格样本，这些样本构成了我们的训练集。 二、成本函数 成本函数（也称为损失函数或代价函数）是衡量模型预测值与实际值之间差异的度量。在单变量线性回归中，我们采用均方误差作为成本函数，公式为： \[ J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 \] 这里，\(m\) 是训练样例的数量，\(h_\theta(x^{(i)})\) 是模型对第i个样例的预测值，\(y^{(i)}\) 是第i个样例的实际价格。 三、参数选择 目标是找到使成本函数最小化的参数 \(\theta_0\) 和 \(\theta_1\)。这可以通过梯度下降法或正规方程等优化算法实现。梯度下降通过迭代更新参数，逐步减小成本函数，直到达到局部最小值或全局最小值。而正规方程则直接求解最小化成本函数的最优参数，适用于样本数量不大的情况。 四、直观理解成本函数 成本函数的直观解释是，它计算了所有训练样例预测值与真实值之差的平方和的平均值。当模型预测值接近实际值时，成本降低；反之，如果预测误差较大，成本上升。通过调整模型参数，我们希望使所有样例的预测误差尽可能小，从而降低整体的成本。 总结，单变量线性回归是机器学习中用于预测连续变量的基础模型，它通过拟合直线来描述输入与输出的关系，并通过成本函数来评估模型的性能。通过学习和优化这个模型，我们可以更好地理解和掌握机器学习中的基本概念和方法。