没有合适的资源?快使用搜索试试~ 我知道了~
Matlab有关多目标遗传算法和多目标优化-多目标遗传算法.pdf
需积分: 43 84 下载量 113 浏览量
2019-08-12
22:14:17
上传
评论 10
收藏 318KB PDF 举报
温馨提示
Matlab有关多目标遗传算法和多目标优化-多目标遗传算法.pdf 有关多目标遗传算法,,希望对大家有用。 Figure20.jpg Figure21.jpg
资源推荐
资源详情
资源评论

Multiob jective Optimization of Trusses using Genetic Algorithms
Carlos A. Co ello Co ello
y
Alan D. Christiansen
z
y
Engineering Design Centre, University of Plymouth, Plymouth, PL4 8AA, UK
z
Department of Computer Science, Tulane University, New Orleans, LA 70118, USA
Abstract:
In this paper we propose the use of the genetic algorithm (GA) as a tool to solve multiobjective
optimization problems in structures. Using the concept of min-max optimum, a new GA-based multiobjective
optimization technique is proposed and two truss design problems are solved using it. The results produced by
this new approach are compared to those produced by other mathematical programming techniques and GA-based
approaches, proving that this technique generates better trade-os and that the genetic algorithm can be used as a
reliable numerical optimization tool.
Keywords
:
genetic algorithms, multiob jective optimization, vector optimization, multicriteria optimization,
structural optimization, truss optimization
1 Intro duction
In most real-world problems, several goals must b e satised simultaneously in order to obtain an optimal
solution. The multiple ob jectives are typically conicting and non-commensurable, and must b e satised simul-
taneously. For example, we might want to b e able to minimize the total weight of a truss while minimizing
its maximum deection and maximizing its maximum allowable stress. The common approach in this sort of
problem is to cho ose one ob jective (for example, the weight of the structure) and incorp orate the other ob jectives
as constraints. This approach has the disadvantage of limiting the choices available to the designer, making the
optimization pro cess a rather dicult task.
Another common approach is the combination of all the ob jectives into a single ob jective function. This
technique has the drawback of mo delling the original problem in an inadequate manner, generating solutions that
will require a further sensitivity analysis to b ecome reasonably useful to the designer.
A more appropriate approach to deal with multiple ob jectives is to use techniques that were originally designed
for that purpose in the eld of Op erations Research. Work in that area started a century ago, and many approaches
have b een rened and commonly applied in economics and control theory.
This paper addresses the imp ortance of multiob jective structural optimization and reviews some of the basic
concepts and part of the most relevant work in this area. Also, we discuss the suitability of a heuristic technique
inspired by the mechanics of natural selection (the genetic algorithm, or GA) to solve multiob jective optimization
problems. We also intro duce a new metho d, based on the concept of min-max optimum. The new metho d
is compared with other GA-based multiob jective optimization metho ds and some mathematical programming
techniques. We show that the new metho d is capable of nding b etter trade-os among the comp eting ob jectives.
Our approach is tested on two well-known truss optimization problems. We p erform these tests with a computer
program called MOSES, which was develop ed by the authors to exp eriment with new and existing multiob jective
optimization algorithms.
This work was done while the author was at Tulane University.
1

2 Previous Work on Multiob jective Structural Optimization
The rst application of multiob jective optimization concepts in structural mechanics app eared in a 1968 pap er
by Krokosky [35]. In this early pap er, Krokosky devised a method that accommo dates the designer's preference
of the design requirements. In his approach, Krokosky required the most desirable and least desirable values
of each of the decision variables and the dierent levels of desirability of various combinations of such decision
variables provided through a ranking matrix. Krokosky adopted a random search technique to nd the b est
trade-o correlating the dierent ob jectives (i.e., desired values of the decision variables) in terms of the a priori
chosen design parameters. This technique happ ens to b e computationally inecient and impractical b ecause it is
sometimes very dicult, or even imp ossible, to get all the requirements in terms of one quantity [45]. Krokosky's
approach was later applied to the optimal design of sandwich panels [55]. Rao et al. [45] used utility theory to
overcome some of the drawbacks of Krokosky's approach when dealing with optimal material choice problems.
Stadler [58] noted the scientic application of the concept of Pareto optimality to problems of natural structural
shap es. He used this concept to compute optimal initial shap es of uniform shallow arches. Rao et al. [47, 48]
showed signicant work in multiob jective structural optimization with uncertain parameters. Rao was one of the
rst to p oint out the imp ortance of incorp orating concepts from game theory into structural optimization, and used
several mathematical programming techniques such as global criterion, utility function, goal programming, goal
attainment, b ounded ob jective function and lexicographic metho ds, to solve multiob jective structural optimization
problems. A more extended analysis of the use of game theory as a design to ol may b e found in [61], although
no applications are included.
Carmichael [7] prop osed the use of the
"
-constraint metho d to the multiob jective optimum design of trusses.
A more formal treatment of the sub ject wass given by Koski and Silvennoinen [33], who prop osed a numerical
metho d that generates the Pareto optimal set of an isostatic truss, based on the exact solution of bicriterion
subproblems. An extension to this work was published later [34] by the same authors. In this latter pap er the
authors prop osed the scalarization of the original multiob jective optimization problem by using norm metho ds
and the reduction of the dimension of the problem by a partial weighting metho d. They used trusses (b oth
isostatic and hyp erstatic) to illustrate these metho ds.
Fu and Frangopol [19] formulated a multiob jective structural optimization technique based on structural reli-
ability theory. This approach was illustrated solving a hyperstatic truss and a frame system. El-Sayed et al. [12]
used linear goal-programming techniques with successive linearizations to solve nonlinear structural optimization
problems. Their application was a three bar truss with uncertainties in b oth load magnitude and direction.
Ha jela and Shih [29] presented a slight variation of the global criterion approach, used in conjunction with
a branch and b ound algorithm, to solve multiob jective optimization problems that involve a mix of continuous,
discrete and integer design variables. A simply supp orted I-b eam and a comp osite laminated b eam were included
to exemplify their approach. Another variant of the global criterion approach was suggested by Saravanos and
Chamis [52] to design lightweight, low-cost comp osite structures. Tseng and Lu [60] applied goal programming,
compromise programming and the surrogate trade-o metho d to the selection of system parameters and large
scale structural design optimization problems.
Grandhi et al. [25] presented a reliability-based decision criterion approach for multiob jective optimization
of structures with a large numb er of design variables and constraints. Lounis and Cohn [38] used a pro jected
Lagrangian algorithm to transform the multiob jective optimization of prestressed concrete structures into a single-
ob jective optimization problem.
Finally, the b o ok by Eschenauer et al. [13] is a very valuable guide to some of the most relevant work in
multiob jective design optimization in the last few years. Go o d surveys on multiob jective structural optimization
may b e found in Stadler [59], Duckstein [11] and Co ello [10].
3 Basic Concepts
Multiob jective optimization (also called multicriteria optimization, multiperformance or vector optimization)
can b e dened as the problem of nding [41]:
a vector of decision variables which satises constraints and optimizes a vector function whose elements
2
F
f
f
f f(x (x
(x
(x
1
*
)
1
*
)
2
)
2
)
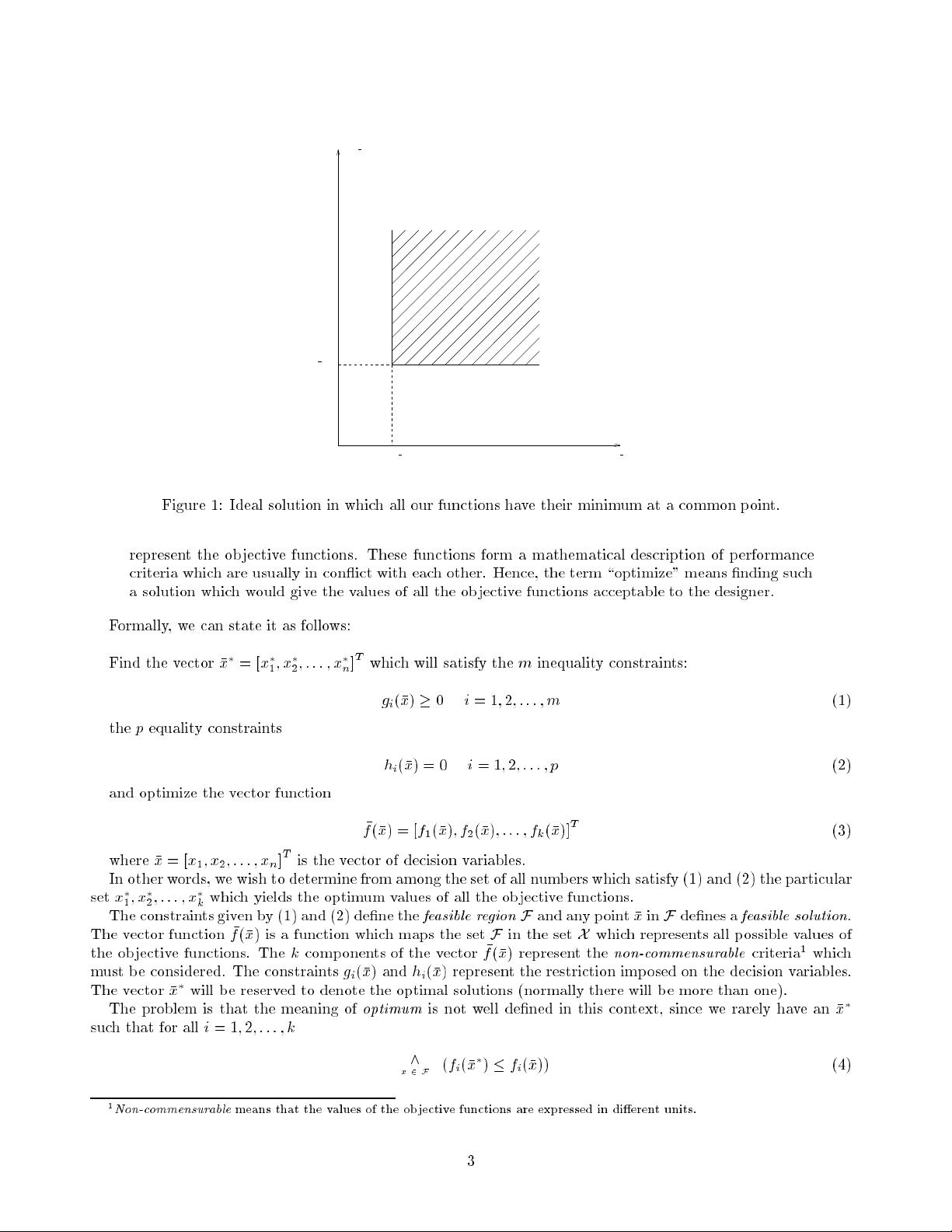
Figure 1: Ideal solution in which all our functions have their minimum at a common p oint.
represent the ob jective functions. These functions form a mathematical description of performance
criteria which are usually in conict with each other. Hence, the term \optimize" means nding such
a solution which would give the values of all the ob jective functions acceptable to the designer.
Formally, we can state it as follows:
Find the vector
x
= [
x
1
; x
2
; : : : ; x
n
]
T
which will satisfy the
m
inequality constraints:
g
i
(
x
)
0
i
= 1
;
2
; : : : ; m
(1)
the
p
equality constraints
h
i
(
x
) = 0
i
= 1
;
2
; : : : ; p
(2)
and optimize the vector function
f
(
x
) = [
f
1
(
x
)
; f
2
(
x
)
; : : : ; f
k
(
x
)]
T
(3)
where
x
= [
x
1
; x
2
; : : : ; x
n
]
T
is the vector of decision variables.
In other words, we wish to determine from among the set of all numb ers which satisfy (1) and (2) the particular
set
x
1
; x
2
; : : : ; x
k
which yields the optimum values of all the ob jective functions.
The constraints given by (1) and (2) dene the
feasible region
F
and any p oint
x
in
F
denes a
feasible solution
.
The vector function
f
(
x
) is a function which maps the set
F
in the set
X
which represents all p ossible values of
the ob jective functions. The
k
comp onents of the vector
f
(
x
) represent the
non-commensurable
criteria
1
which
must b e considered. The constraints
g
i
(
x
) and
h
i
(
x
) represent the restriction imp osed on the decision variables.
The vector
x
will be reserved to denote the optimal solutions (normally there will be more than one).
The problem is that the meaning of
optimum
is not well dened in this context, since we rarely have an
x
such that for all
i
= 1
;
2
; : : : ; k
^
x
2 F
(
f
i
(
x
)
f
i
(
x
)) (4)
1
Non-commensurable
means that the values of the ob jective functions are expressed in dierent units.
3

If this was the case, then
x
would b e a desirable solution, but we normally never have a situation like this, in
which all the
f
i
(
x
) have a minimum in
F
at a common p oint
x
. An example of this ideal situation is shown in
Figure 1. However, since this situation rarely happ ens in real-world problems, then we have to establish a certain
criteria to determine what would b e considered as an \optimal" solution.
3.1 Pareto Optimum
The concept of
Pareto optimum
was formulated by Vilfredo Pareto in 1896 [42], and constitutes by itself the
origin of research in multiob jective optimization. We say that a p oint
x
2 F
is
Pareto optimal
if for every
x
2 F
either,
^
i
2
I
(
f
i
(
x
) =
f
i
(
x
)) (5)
or, there is at least one
i
2
I
such that
f
i
(
x
)
> f
i
(
x
) (6)
In words, this denition says that
x
is Pareto optimal if there exists no feasible vector
x
which would decrease
some criterion without causing a simultaneous increase in at least one criterion. Unfortunately, the Pareto
optimum almost always gives not a single solution, but rather a set of solutions called
non-inferior
or
non-
dominated
solutions.
3.2 Pareto Front
The minima in the Pareto sense are going to b e in the b oundary of the design region, or in the lo cus of the
tangent p oints of the ob jective functions. This region is called the
Pareto Front
. In general, it is not easy to nd
an analytical expression of the line or surface that contains these p oints, and the normal pro cedure is to compute
the points
F
k
and their corresponding
f
(
F
k
). When we have a sucient amount of these, we may proceed to
take the nal decision.
3.3 Min-Max Optimum
The idea of stating the
min-max optimum
and applying it to multiob jective optimization problems, was taken
from game theory, which deals with solving conicting situations. The min-max approach to a linear mo del was
prop osed by Jutler [40] and Solich [40]. It has been further develop ed by Osyczka [39], Rao [46] and Tseng and
Lu [60].
The min-max optimum compares relative deviations from the separately attainable minima. Consider the
i
th
ob jective function for which the relative deviation can b e calculated from
z
0
i
(
x
) =
j
f
i
(
x
)
?
f
0
i
j
j
f
0
i
j
(7)
or from
z
00
i
(
x
) =
j
f
i
(
x
)
?
f
0
i
)
j
j
f
i
(
x
)
j
(8)
It should b e clear that for (7) and (8) we have to assume that for every
i
2
I
and for every
x
2 F
,
f
i
(
x
)
6
= 0.
If all the ob jective functions are going to b e minimized, then equation (7) denes function relative increments,
whereas if all of them are going to b e maximized, it denes relative decrements. Equation (8) works conversely.
Let
z
(
x
) = [
z
1
(
x
)
; : : : ; z
i
(
x
)
; : : : ; z
k
(
x
)]
T
b e a vector of the relative increments which are dened in
R
k
. The
comp onents of the vector
z
(
x
) will b e evaluated from the formula
8
i
2
I
(
z
i
(
x
)) =
max
f
z
0
i
(
x
)
; z
00
i
(
x
)
g
(9)
4
剩余25页未读,继续阅读
资源评论

weixin_39840650
- 粉丝: 413
- 资源: 1万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功