ExploringStructuralConsistencyinGraphRegularizedJointSpectral-SpatialSparseCodingforHyperspectralImageClassification资源-CSDN文库

95 浏览量 2021-02-22 00:24:42 上传评论收藏 1.69MB PDF 举报

Exploring Structural Consistency in Graph Regularized Joint Spectral-Spatial Sparse Coding for Hyperspectral Image Classification 在超光谱图像分类领域中，谱间和空间数据的分布对于描述和识别图像中的不同材料和物体是至关重要的。此外，跨波段一致的空间结构有助于捕捉物体的固有结构信息。这意味着，在使用稀疏编码方法重建图像时，需要考虑三个属性：不同地面物体的分布导致在不同空间位置有不同的编码系数；由于不同物体材料的反射特性不同，局部空间结构在不同波段间略有变化；最后也是最重要的是，必须在各个波段间强制保持某种结构一致性，以反映同一物体在图像的各个波段上位于同一空间位置的事实。基于以上考虑，本文提出了一种新颖的联合谱-空间稀疏编码模型，用于探索超光谱图像分类中的结构一致性。对于每个波段图像，我们采用稀疏编码步骤来重建波段图像中的结构。这允许生成不同的字典来表征波段间的图像变化。同时，我们强制在不同波段的相同空间位置保持相同的编码系数，以维持波段间的结构一致性。为了进一步提升模型的区分能力，我们将图拉普拉斯稀疏约束融入模型中，以确保在字典生成步骤中保持谱间一致性。实验结果表明，所提出的方法在性能上优于一些最先进的谱-空间稀疏编码方法。我们需要了解超光谱成像是一种遥感技术，它可以在成百上千的连续光谱波段中捕获图像，从而提供了关于地球表面材料和物体非常丰富的光谱信息。与传统的多光谱成像相比，超光谱成像的一个关键优势是其提供的高光谱分辨率，这使得区分和识别地面上不同类型的物质变得更加精确。稀疏编码是一种信号处理方法，其核心思想是通过一个稀疏基来表示信号，使表示中大部分系数都为零或接近零，而只有少数系数是非零的。在超光谱图像分类的应用中，稀疏编码可以用来重构图像，同时提取图像中的有效特征。结构一致性是图像处理中的一个重要概念，特别是在多模态图像融合或图像序列处理中，指的是在多个图像中保持相同物体或结构在空间和光谱上的对应关系。在超光谱图像的上下文中，结构一致性意味着在不同波段上物体应该具有相同的边缘、形状和纹理特征。接下来，图拉普拉斯稀疏约束是一个图信号处理的概念，它利用图结构来表示数据，并应用图拉普拉斯算子来增强数据的局部特性。在这个超光谱图像分类的模型中，图拉普拉斯正则化器被用来确保在字典生成过程中保持光谱一致性，这有助于模型更好地学习和保持不同波段之间光谱特征的一致性。本文提出的联合谱-空间稀疏编码模型不仅关注图像的空间结构，而且考虑了不同波段之间的结构关系。这意味着模型不仅仅是独立地从每个波段中提取特征，而是通过在波段之间施加约束，来保留和利用同一物体在各个波段上的一致性信息。这有助于减少分类错误，并提高分类的准确性。为了验证该模型的有效性，作者进行了实验，并将结果与现有的几种最先进的谱-空间稀疏编码方法进行了比较。实验结果表明，所提出的模型在分类准确率上优于这些对比方法，从而证明了结构一致性考虑在超光谱图像分类中的重要性。这篇文章对超光谱图像分类的研究做出了有意义的贡献，特别是在提升分类准确性方面，通过考虑波段间结构的一致性以及引入图拉普拉斯正则化来强化光谱一致性。这种方法不仅在理论上具有创新性，而且在实践中展示了较高的应用价值。

资源推荐

资源详情

资源评论

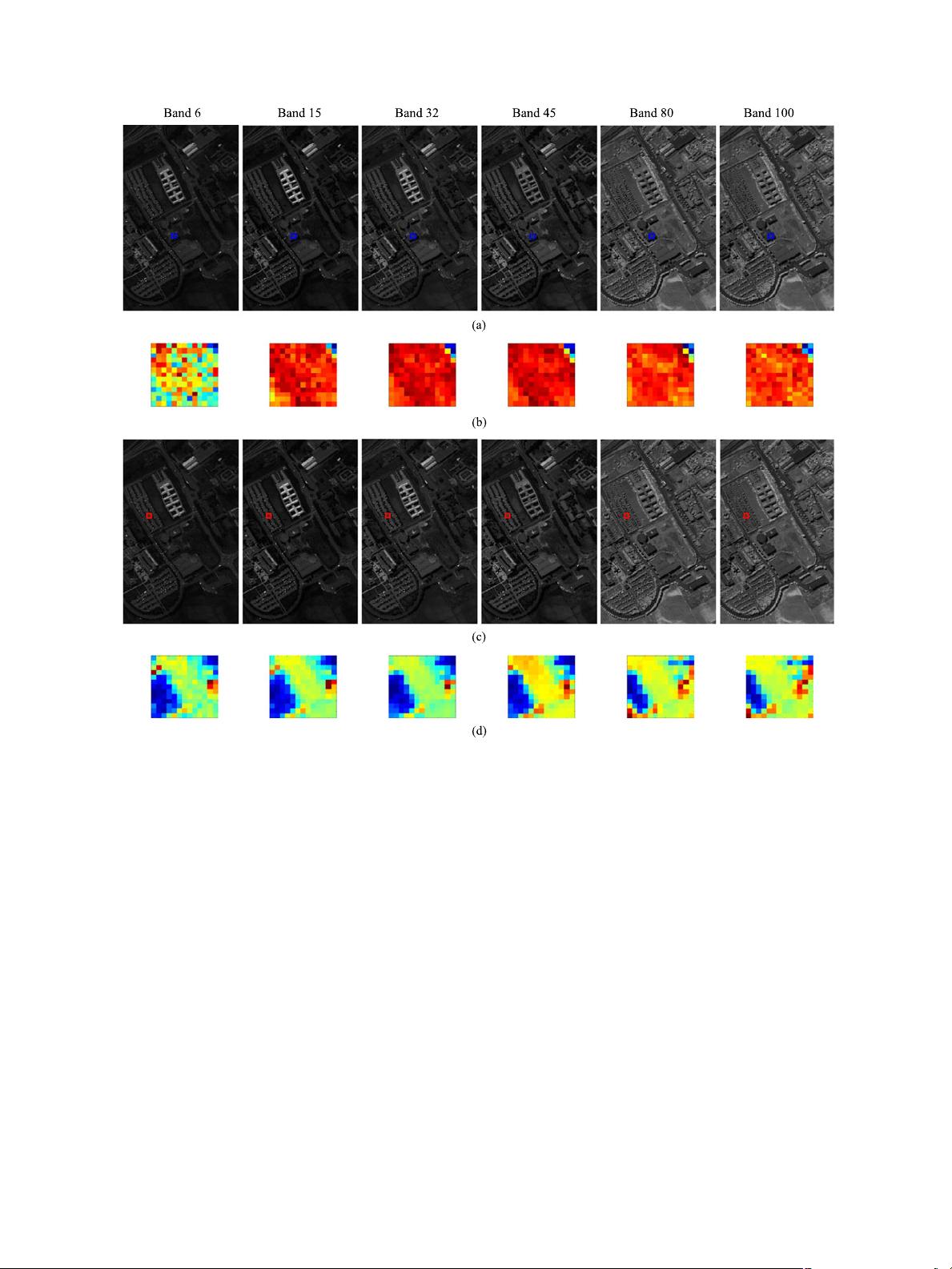
IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING, VOL. 10, NO. 3, MARCH 2017 1151

Exploring Structural Consistency in Graph

Regularized Joint Spectral-Spatial Sparse Coding

for Hyperspectral Image Classiﬁcation

Changhong Liu, Jun Zhou, Senior Member, IEEE, Jie Liang, Yuntao Qian, Member, IEEE, Hanxi Li,

and Yongsheng Gao, Senior Member, IEEE

Abstract—In hyperspectral image classiﬁcation, both spectral

and spatial data distributions are important in describing and iden-

tifying different materials and objects in the image. Furthermore,

consistent spatial structures across bands can be useful in captur-

ing inherent structural information of objects. These imply that

three properties should be considered when reconstructing an im-

age using sparse coding methods. First, the distribution of different

ground objects leads to different coding coefﬁcients across the spa-

tial locations. Second, local spatial structures change slightly across

bands due to different reﬂectance properties of various object ma-

terials. Finally and more importantly, some sort of structural con-

sistency shall be enforced across bands to reﬂect the fact that the

same object appears at the same spatial location in all bands of

an image. Based on these considerations, we propose a novel joint

spectral-spatial sparse coding model that explores structural con-

sistency for hyperspectral image classiﬁcation. For each band im-

age, we adopt a sparse coding step to reconstruct the structures in

the band image. This allows different dictionaries be generated to

characterize the band-wise image variation. At the same time, we

enforce the same coding coefﬁcients at the same spatial location

in different bands so as to maintain consistent structures across

bands. To further promote the discriminating power of the model,

we incorporate a graph Laplacian sparsity constraint into the

model to ensure spectral consistency in the dictionary generation

step. Experimental results show that the proposed method outper-

forms some state-of-the-art spectral-spatial sparse coding methods.

Index Terms—Graph Laplacian regularizer, hyperspectral im-

age, sparse coding, structural consistency.

Manuscript received April 15, 2016; revised July 9, 2016 and August 10,

2016; accepted August 11, 2016. Date of publication September 8, 2016; date

of current version February 13, 2017. This work was supported by the Australian

Research Council Linkage under Project LP150100658, the National Natural

Science Foundation of China under Grant 61571393, Grant 61462042, Grant

61365002, and Grant 61262036, and the Visiting Scholars Special Funds from

Young and Middle-aged Teachers Development Program for Universities in

Jiangxi Province. (Corresponding author: Jun Zhou.)

C. Liu and H. Li are with the School of Computer and Information Engineer-

ing, Jiangxi Normal University, Nanchang 330022, China (e-mail: ahong286@

126.com; hanxi.li@nicta.com.au).

J. Zhou is with the School of Information and Communication Technol-

ogy, Grifﬁth University, Brisbane, QLD 4111, Australia (e-mail: jun.zhou@

grifﬁth.edu.au).

J. Liang is with the School of Engineering, Australian National University,

Canberra, ACT 0200, Australia (e-mail: jie.liang@anu.edu.au).

Y. Qian is with the Institute of Artiﬁcial Intelligence, College of

Computer Science, Zhejiang University, Hangzhou 310027, China (e-mail:

ytqian@zju.edu.cn; yuntaoq@yahoo.com.cn).

Y. Gao is with the School of Engineering, Grifﬁth University, Brisbane, QLD

4111, Australia (e-mail: yongsheng.gao@grifﬁth.edu.au).

Color versions of one or more of the ﬁgures in this paper are available online

at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/JSTARS.2016.2602305

I. INTRODUCTION

EMOTE sensing hyperspectral images (HSI) are acquired

in hundreds of bands to measure the reﬂectance of earth

surface, discriminate various materials, and classify ground ob-

jects. HSI classiﬁcation aims at assigning each pixel with one

thematic class in a scene [1]. Various machine learning models

have been proposed for this purpose, such as Bayesian model [1],

random forest [2], neural networks [3], support vector machines

(SVM) [4]–[7], sparse representation [8]–[13], and deep learn-

ing [14], [15].

Many HSI classiﬁcation methods make prediction based on

the spectral response at a single pixel [6], [8], [9], [16]–[19].

While spectral information is essential in image classiﬁcation

and material identiﬁcation, information extracted from spatial

domain is very useful to discriminate various targets made of

the same materials [20], [21]. To address this need, spectral-

spatial HSI classiﬁcation approaches have been reported, each

type of approach exploring and exploiting different ways to in-

tegrate spatial features with spectral features. Mura et al. and

Ghamisi et al. proposed mathematical morphology methods to

analyze spatial relationships between pixels using structured el-

ements [22], [23]. Markov random ﬁeld methods considered

spatial information by adding to the objective function a term

that deﬁnes spatial correlations in the prior model [24], [25].

Qian et al. developed three-dimensional (3-D) discrete wavelet

transform to extract 3-D features along spectral and spatial di-

mensions simultaneously [26]. Moreover, many researchers pro-

posed sparse representation methods to include spatial sparsity

constraints or Kernel function to integrate spectral and spatial

features [10], [12], [27]–[31].

Among these approaches, sparse representation-based

classiﬁers have achieved the state-of-the-art performance [27],

[32]. They provide an effective way of modeling the spatial

neighborhood relationship and the distribution of atoms in the

spectral or spatial domain, so that both spectral and spatial

information can be seamlessly integrated and modeled. In

sparse representation, a test sample is treated as a linear

combination of atoms from training s amples or a learned

dictionary. A sparse regularization term is normally included

to learn a discriminative representation of images [33]–[35].

Recently, structured sparsity priors are also incorporated into

reconstruction methods [12], [36]–[39]. These include joint

sparsity constraint [40], group sparsity constrain [41], graph

See http://www.ieee.org/publications

standards/publications/rights/index.html for more information.

1152 IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING, VOL. 10, NO. 3, MARCH 2017

Fig. 1. Consistent structures in the University of Pavia dataset. (a) Pixel (362, 149) in bands 6, 15, 32, 45, 80, and 100 for the “Bitumen” class. (b) 13 ×13

patches centered at pixel (362, 149). (c) Pixel (251, 76) in bands 6, 15, 32, 45, 80, and 100 for the “Bricks” class. (d) 13 × 13 patches centered at pixel (251, 76).

Laplacian sparsity constraint [36], low-rank constraint [42],

and low-rank group sparsity constraint [12]. Graph Laplacian

sparsity constraint is based on the spatial dependencies between

the neighboring pixels [12], [36]. It preserves the local manifold

structure so that if two data points are close in their original

data space, the sparse representations of these two data points

are also close to each other in the new data space.

Although spectral-spatial analysis has been studied inten-

sively in HSI classiﬁcation, how to explore the local structural

information has not been adequately addressed. To get a deeper

understanding of the structural information embedded in a hy-

perspectral image, we use the University of Pavia image in

Fig. 1 as an example. In the ﬁrst row, bands 6, 15, 32, 45, 80,

and 100 are displayed. In the second and fourth rows, small

patches extracted from neighborhoods around pixels (362, 149)

and (251, 76) are displayed, respectively. Three observations can

be obtained from this ﬁgure. First, various land cover classes

have different distributions in the spatial domain. This happens

in all bands. Second, local spatial structures change slightly

across different bands. This is due to the distinct reﬂectance

properties of object materials at different light wavelength. As a

consequence, the extracted Gabor features at the same location

in different bands also change slightly. Finally and more im-

portantly, some sort of structural consistency can be observed

across bands, as the ground objects at each location are consis-

tent in all bands. Such consistency has been proved to be useful

in hyperspectral image denoising [43]. In general, image repre-

sentation and classiﬁcation models shall be able to address all

these observations.

Motivated by the above observations, we propose a novel

joint spectral-spatial framework to explore structural consis-

tency along all bands in the s parse coding model. For each

band image, image patches or 2-D image features centered

at pixels are ﬁrst extracted from local neighborhood, which

contain local structures of the central pixels. Then a sparse

coding step is adopted to reconstruct the structures in the band

images. This allows different dictionaries to be generated to

characterize the band-wise image variation. At the same time,

LIU et al.: EXPLORING STRUCTURAL CONSISTENCY IN GRAPH REGULARIZED JOINT SPECTRAL-SPATIAL SPARSE CODING 1153

consistent structures across bands are maintained by enforcing

the same coding coefﬁcients at t he same spatial location in

different bands. To further promote the discriminating power of

the model, a graph Laplacian sparsity constraint is incorporated

into the model to ensure spectral consistency in the dictionary

generation step. At last, the learned coefﬁcients are fed into the

classiﬁer for pixel-wise classiﬁcation.

The contribution of this paper lies in two aspects. First, we

propose a novel joint spectral-spatial s parse coding framework,

which can explore the structural consistency along all bands and

integrate the spectral information and spatial structures into a

sparse coding framework. Under this framework, 2-D structural

features can be applied to HSI classiﬁcation effectively and di-

rectly, and the learned coefﬁcients inherently contain both s pec-

tral characteristics and spatial structures of HSI images. Second,

we extend this model by including a graph regularization term to

preserve the spectral relations between data points. This allows

better relationship between data to be modeled, which improves

the classiﬁcation performance.

The rest of this paper is organized as follows. In Section II, we

review related work on sparse representation-based hyperspec-

tral image classiﬁcation. In Section III, we ﬁrst brieﬂy introduce

the basic sparse coding model. Then we describe the proposed

method that preserves structural consistency, its graph-based

extension, and the optimization algorithm for learning sparse

coefﬁcient and dictionaries. Experimental results are presented

in Section IV. We conclude our work and point out future re-

search direction in Section V.

II. R

ELATED WORK

Recently, sparse representation has been widely used in HSI

classiﬁcation. It allows spectral information be combined with

spatial information, so that discriminative image representation

can be achieved. Some of them directly extract the spectral-

spatial features and then feed these features into the sparse rep-

resentation model. Qian et al. extracted a 3-D discrete wavelet

transform (3-D-DWT) texture features to capture geometrical

and statistical spectral-spatial structures and then applied them

to the sparse representation model [26]. He et al. proposed an

minimization-based spectral-spatial classiﬁcation method. A

spatial translation invariant wavelet sparse representation [13]

was adopted in the model. Yang et al. combined Gabor spa-

tial features and nonparametric weighted spectral features, and

then applied sparse representation to describe the HSI [11]. To

selected the most representative Gabor cube features for im-

age classiﬁcation, Jia et al. proposed to use Fisher discrimina-

tion criterion and a multitask joint sparse representation frame-

work [31].

Structured sparsity constraints [12], [36], [40]–[42] are of-

ten incorporated into sparse representation to improve the per-

formance of HSI classiﬁcation. These methods explore the

spatial dependencies between neighboring pixels, or the inher-

ent structure of dictionary, or both [12]. For example, Lapla-

cian constraint has been incorporated into the sparse recovery

optimization problem such that the reconstructed neighboring

pixels have similar spectral characteristics [44]. In [26], Qian

et al. used sparsity constraints to help selecting the discriminant

features from a pool of 3-D-DWT texture features. Low rank

sparse representation methods have also been proposed to ex-

plore the spatial correlations of neighboring pixels [12], [45].

The sparse representation is further extended into kernel-

ized or joint sparse form to exploit the spatial correlation

across neighboring pixels. Chen et al. used simultaneous sub-

space pursuit method, simultaneous orthogonal matching pur-

suit (SOMP), and their kernelized extension for spectral-spatial

HSI classiﬁcation [10], [44]. He et al. utilized empirical mode

decomposition and morphological wavelet transform to extract

spectral-spatial features, which were then integrated by a sparse

multitask learning method [28]. Liu et al. proposed a neighbor-

ing ﬁltering Kernel sparse representation for enhanced classiﬁ-

cation of HSIs [27]. The relationship between pixels in a local

neighborhood can also be modeled by structural similarity [29],

graph embedding [32], and set-to-set distance [46]. When joint

sparse representation is concerned, Zhang et al. constructed mul-

tiple features and enforced pixels in a small region to share the

same sparsity pattern for each type of feature [47]. Wang et al.

presented a spatial-spectral derivative-aided Kernel joint sparse

representation, which considered high order spatial context and

distinct spectral information [30].

Most aforementioned methods combine spectral informa-

tion with spatial information using spatial constraints, complex

spectral-spatial features, or joint sparse form of neighborhood

pixels, and then make classiﬁcation by minimizing the residual

between a testing sample and the reconstructed image. Unlike

the sparse representation procedure, Farani and Rabiee [48] pro-

posed a sparse coding method for HSI classiﬁcation, which used

a spatially weighted sparse unmixing approach as a front-end

and the learned sparse codes as the input to a linear SVM. Simi-

lar to this work, in our method, we also use learned sparse codes

as inputs to the the classiﬁer. This is done by ﬁrst extracting

2-D spatial features from local neighborhoods and the learning

band-wise distinct dictionary. Finally, we force the same spatial

location in different bands share the same coding coefﬁcients to

capture the structural consistency along all bands.

III. SCSC

FOR HSI CLASSIFICATION

In an HSI, the distributions of spatial structures vary in dif-

ferent spatial locations, but are closely related to each other in

different bands. Such structural consistency has been shown in

Fig. 1. Considering the spatial correlation along the spectral

dimension, we construct a joint spectral-spatial sparse coding

model with structural consistency by assigning the same coef-

ﬁcient in the same position of different bands. The modeling

process also preserves the distinct band characteristics by pro-

ducing band-wise dictionaries. The framework of the proposed

SCSC method is shown in Fig. 2.

At each pixel, local spatial feature is ﬁrst extracted band by

band. Though any type of 2-D feature can be used here, we

adopted a s imple solution by extracting image patch centered at

the pixel. Then, the dictionaries on all bands are trained individ-

ually and simultaneously with the same coefﬁcient across bands.

That is to say, the bth dictionary is learned only using the spatial

剩余13页未读，继续阅读

评论收藏

内容反馈

weixin_38750007

粉丝: 4
资源: 920

Exploring Structural Consistency in Graph Regularized Joint Spec...

最新资源

Exploring Structural Consistency in Graph Regularized Joint Spec...

Paper Reading — 《Spectral-Spatial Attention Networks for Hyperspectral Image Classification》

Hyperspectral Image Classification by Spatial-Spectral Derivative-Aided Kernel Joint Sparse Representation

classification of hyperspectral image data

Exploring the Road to 6G： ABC-Foundation for Intelligent Mobile

Exploring-Arduino-Tools-and-Techniques-for-Engineering-Wizardry-1st-Edition

Exploring Faster-than-Nyquist for Satellite Direct Broadcasting

机器学习论文合集（pdf格式）.zip

Programming 32-bit Microcontrollers in C Exploring the PIC32

Exploring the Road to 6G： ABC-Foundation for Intelligent Mobile Networks.pdf

Web Data Mining - Exploring Hyperlinks, Contents, and Usage Data-2007

CLIPDraw - Exploring Text-to-Drawing Synthesis through Language-Image Encoders

现代数字通信论文1

Exploring C++ 11(2nd Edition 2013)-master_C++11_

expect教程大全(exploring expect、expect教程中文版等7本教程)

Exploring Expect (A Tcl-based Toolkit for Automating Interactive Programs)

Art-Exploring-the-New-Android-KitKat-Runtime

Practical Machine Learning and Image Processing

Data-driven Graphic Design Creative Coding for Visual Communication

Exploring the location of object deleted by seam-carving

Bidirectional Rapidly-exploring Random Trees_random_RRT_rrtmatla

Exploring Randomly Wired Neural Networks for Image Recognition

Exploring Arduino- Tools and Techniques for Engineering Wizardry

Ubuntu Hacks - Tips and Tools for Exploring, Using, and Tuning Linux

最新资源