没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
微分相位衬度计算机层析成像法(DPC-CT)是一种新的X射线无损检测方法。与传统方法相比,该方法在检测弱吸收物质时优势明显。但DPC-CT技术需要进行多次扫描后才能获取足够的样品信息,这必将导致很长的辐射时间和巨大的辐射剂量。因此,研究在稀疏角度条件下的DPC-PC重建算法就显得尤为重要。分析了DPC-CT的特点,在凸集投影(POCS)的理论框架下,将L1范数、曲波系数约束和经典的代数迭代算法(ART)相结合提出了一种适合DPC-CT的重建算法。数值模拟和实验的结果表明,该方法可以根据少量投影数据获得较好的重建结果。
资源推荐
资源详情
资源评论

书书书
第
34
卷
第
1
期
光
学
学
报
Vol.34
,
No.1
2014
年
1
月
犃犆犜犃犗犘犜犐犆犃犛犐犖犐犆犃
犑犪狀狌犪狉
狔
,
2014
基于
犔
1
范数和曲波系数双约束的稀疏角度
微分相位衬度计算机层析成像重建方法
李梦婕
李
镜
孙
怡
(大连理工大学信息与通信工程学院,辽宁 大连
116024
)
摘要
微分相位衬度计算机层析成像法(
DPCCT
)是一种新的
X
射线无损检测方法。与 传 统 方 法 相 比,该 方 法 在
检测弱吸收物质时优势明显。但
DPCCT
技术需要进行多次扫描后才能获取足够的样品 信 息,这必将导致很长的
辐射时间和巨大的辐射剂量。因此,研究 在 稀 疏 角 度 条 件 下 的
DPCPC
重 建 算 法 就 显 得 尤 为 重 要。 分 析 了
DPC
CT
的特点,在凸集投影(
POCS
)的理论框架下,将
犔
1
范数、曲波系数约束和经典的代数迭代算法(
ART
)相 结 合 提
出了一种适合
DPCCT
的重建算法。数值模拟和实验的结果表明,该方法可以根据少量投 影 数 据 获 得 较 好 的 重 建
结果。
关键词
成像系统;微分相位衬度计算机层析成像;稀疏表达;凸集投影法;
犔
1
范数;曲波变换
中图分类号
O434.19
文献标识码
A
犱狅犻
:
10.3788
/
犃犗犛201434.0111003
犛
狆
犪狉狊犲犃狀
犵
狌犾犪狉犇犻犳犳犲狉犲狀狋犻犪犾犘犺犪狊犲犆狅狀狋狉犪狊狋犆狅犿
狆
狌狋犲犱犜狅犿狅
犵
狉犪
狆
犺
狔
犚犲犮狅狀狊狋狉狌犮狋犻狅狀犝狊犻狀
犵
犔
1
犖狅狉犿 犪狀犱犆狌狉狏犲犾犲狋犆狅狀狊狋狉犪犻狀狋狊
犔犻犕犲狀
犵犼
犻犲
犔犻犑犻狀
犵
犛狌狀犢犻
(
犛犮犺狅狅犾狅
犳
犐狀
犳
狅狉犿犪狋犻狅狀犪狀犱犆狅犿犿狌狀犻犮犪狋犻狅狀犈狀
犵
犻狀犲犲狉犻狀
犵
,
犇犪犾犻犪狀犝狀犻狏犲狉狊犻狋
狔
狅
犳
犜犲犮犺狀狅犾狅
犵狔
,
犇犪犾犻犪狀
,
犔犻犪狅狀犻狀
犵
116024
,
犆犺犻狀犪
)
犃犫狊狋狉犪犮狋
犇犻犳犳犲狉犲狀狋犻犪犾
狆
犺犪狊犲犮狅狀狋狉犪狊狋犮狅犿
狆
狌狋犲犱狋狅犿狅
犵
狉犪
狆
犺
狔
(
犇犘犆犆犜
)
犻狊犪狀狅狏犲犾犡狉犪
狔
犻狀狊
狆
犲犮狋犻狅狀犿犲狋犺狅犱狑犺犻犮犺犺犪狊
狅犫狏犻狅狌狊犪犱狏犪狀狋犪
犵
犲犻狀犱犲狋犲犮狋犻狀
犵
狑犲犪犽犪犫狊狅狉
狆
狋犻狅狀狊狌犫狊狋犪狀犮犲犮狅犿
狆
犪狉犲犱 狑犻狋犺犮狅狀狏犲狀狋犻狅狀犪犾犆犜狉犲犮狅狀狊狋狉狌犮狋犻狅狀 犿犲狋犺狅犱狊.
犎狅狑犲狏犲狉
,
犇犘犆犆犜狌狊狌犪犾犾
狔
狀犲犲犱狋狅狊犮犪狀 犿犪狀
狔
狋犻犿犲狊犻狀狅狉犱犲狉狋狅狅犫狋犪犻狀犲狀狅狌
犵
犺狉犲犳狉犪犮狋犻狅狀犪狀
犵
犾犲犻狀犳狅狉犿犪狋犻狅狀
,
狑犺犻犮犺
犾犲犪犱狊狋狅 狌狀犪犮犮犲
狆
狋犪犫犾
狔
犾狅狀
犵
犲狓
狆
狅狊狌狉犲狋犻犿犲 犪狀犱 犺狌
犵
犲 犡狉犪
狔
犱狅狊犲狊.犜犺狌狊
,
狋犺犲狊狋狌犱
狔
狅犳狊
狆
犪狉狊犲 犪狀
犵
狌犾犪狉 犇犘犆犆犜
狉犲犮狅狀狊狋狉狌犮狋犻狅狀犪犾
犵
狅狉犻狋犺犿犻狊
狆
犪狉狋犻犮狌犾犪狉犾
狔
犻犿
狆
狅狉狋犪狀狋.犃犳狋犲狉犪狀犪犾
狔
狕犻狀
犵
狋犺犲犮犺犪狉犪犮狋犲狉犻狊狋犻犮狊狅犳狋犺犲犇犘犆犆犜.犅犪狊犲犱狅狀狋犺犲
狋犺犲狅狉犲狋犻犮犪犾犳狉犪犿犲狑狅狉犽狅犳
狆
狉狅
犼
犲犮狋犻狅狀狅狀犮狅狀狏犲狓狊犲狋
(
犘犗犆犛
),
犪狉犲犮狅狀狊狋狉狌犮狋犻狅狀犪犾
犵
狅狉犻狋犺犿犳狅狉犇犘犆犆犜犻狊
狆
狉狅
狆
狅狊犲犱犫
狔
犮狅犿犫犻狀犻狀
犵
犔
1
狀狅狉犿
,
犮狌狉狏犲犾犲狋犮狅犲犳犳犻犮犻犲狀狋犮狅狀狊狋狉犪犻狀狋犪狀犱 犱犪狊狊犻犮犪犾犪犾
犵
犲犫狉犪狉犲犮狅狀狊狋狉狌犮狋犻狅狀狋犲犮犺狀犻
狇
狌犲
(
犃犚犜
)
.犜犺犲
狀狌犿犲狉犻犮犪犾狊犻犿狌犾犪狋犻狅狀犪狀犱犲狓
狆
犲狉犻犿犲狀狋犪犾狉犲狊狌犾狋狊狊犺狅狑狋犺犪狋狋犺犲
狆
狉狅
狆
狅狊犲犱犪犾
犵
狅狉犻狋犺犿犮犪狀狊犻
犵
狀犻犳犻犮犪狀狋犾
狔
犻犿
狆
狉狅狏犲狋犺犲犻犿犪
犵
犲
狇
狌犪犾犻狋
狔
狅犳狋犺犲狊
狆
犪狉狊犲犪狀
犵
狌犾犪狉犇犘犆犆犜狉犲犮狅狀狊狋狉狌犮狋犻狅狀狊.
犓犲
狔
狑狅狉犱狊
犻犿犪
犵
犻狀
犵
狊
狔
狊狋犲犿狊
;
犱犻犳犳犲狉犲狀狋犻犪犾
狆
犺犪狊犲犮狅狀狋狉犪狊狋犮狅犿
狆
狌狋犲犱狋狅犿狅
犵
狉犪
狆
犺
狔
;
狊
狆
犪狉狊犲犲狓
狆
狉犲狊狊犻狅狀
;
狆
狉狅
犼
犲犮狋犻狅狀狅狀
犮狅狀狏犲狓狊犲狋
;
犔
1
狀狅狉犿
;
犮狌狉狏犲犾犲狋
犗犆犐犛犮狅犱犲狊
110.6955
;
100.3010
;
100.6950
;
200.3050
;
040.7480
收稿日期:
20130726
;收到修改稿日期:
20130816
基金项目:国家自然科学基金(
61071210
)
作者简介:李梦婕(
1989
—),女,硕士研究生,主要从事图像处理方面的研究。
Email
:
lm
j
men
g
1
@
126.com
导师简介:孙
怡(
1964
—),女,博士,教授,主要从事光电信息检测、图像处理与模式识别等方面的研究。
Email
:
lslwf
@
dlut.edu.cn
(通信联系人)
1
引
言
对于弱吸收物 质,
X
射线 相 衬成 像 方 法 使 用 折
射信息,而不是衰减信息作为成像信号,这样可以提
供更加丰富的关于物体内部结构的信息。到现在为
止,
X
射线相衬成像技术已经发展出
4
大类方法:干
涉成像法、衍射增强成像法(
DEI
)、相位传播 法和光
栅成像法。在这些 方 法中,后 两 种方 法 的优 势 在于
它们都可以采用宽 带 非单 色 光源
,而 前 两种 方 法则
01110031
光
学
学
报
对射线的平行性与相干性要求非常高。但相较于光
栅成像法,相位传播法 对 光源 的 空间 相 干性 有 较高
的要求,因此被局限于功率较低的微焦点源,光栅成
像法较好地解决了 这 个问 题,显示 出 较强 的 应用 前
景。干涉成像法可以测量
X
射线的 相位分 布,相 位
传播法可以测量
X
射线相 位的二 阶梯度 分布,衍 射
增强成像法和 光 栅 成 像 法 则 可 以 测 量
X
射 线 相 位
的一阶梯度分布
。因 此,衍射 增强 成 像法 和 光栅 成
像法常被统称为微分相位衬度 (
DPC
)成像法,而基
于这两种成像方 法 的计 算 机断 层 成像 (
CT
)技 术 称
为
DPCCT
。无 论 是
DEI
还 是 光 栅 成 像 法 所 得 到
的都不是直接的相 位 信息,而 是 包含 相 位信 息 的投
影像,均需要对物体进行多次扫描,通过信息分离方
法来得到相位的一 阶 导数 信 息,而此 过程 必 将导 致
极大的辐射剂量与过长的辐射时间。因此研究稀疏
角度下的 重 建 算 法 对
DPCCT
有 着 重 要 意 义。 目
前,
DPCCT
重建算法大致可分为两大类,第一类算
法主张恢复出物体的相位项
δ
[
1-2
]
,第二类算法主张
恢复出相位项梯度
δ
[
3-4
]
,本文针对第二 类算法 展
开研究。
与传统
CT
类 似,
DPCCT
也 可 以 归 结 为 求 解
线性方程组的问 题。 在稀 疏 角度 条 件下,由 于 数据
量的缺失,观测数据个数远小于待恢复的像素个数。
此时,满足该方程组的解有无穷多个,而待重建图像
只是这些解当中 的 一个。因 此,往往 需要 加 入恰 当
的约束条件,从满足方 程 组的 解 当中 选 择一 个 满足
约束条件的解。或者说需要将该问题归结为约束优
化问题。基于集 合 理论 的 凸集 投 影法 (
POCS
)
[
5
]
是
约束优化问题的一 个 著名 方 法,这种 理论 将 观测 数
据一致性以及其他 约 束条 件 视为 若 干集 合,解空 间
就是这些集合的 交 集。 值 得 一提 的 是,约束 条件 往
往需要根据具体问题的特点选择。众所周知,在图
像处理领域
,小波变换因具备良好的多分辨率特性、
时频局域性以及对光滑奇异性函数的最优逼近性等
特征而得到了 广泛 的 应用。然 而在 大 多数 情 况下,
函数的奇异性(边缘不连续的线状特征)不仅仅是点
奇异,更多的则表现为线奇异、面奇异。在这种情况
下,小波变换已不能精 确 地表 达 图像 边 缘线 段 的方
向及线状特征等
,因 此 小波 变 换会 在 边缘 或 细节 位
置出现模糊
。为了提取高维函数的奇异性这类有效
信息,
Candes
等
[
6-7
]
利 用 多 尺 度 几 何 分 析 的 思 想,
相继提出了第一代 和 第二 代 曲波,并 构 造了 曲 波的
紧框架,对于具有光滑奇异性曲线的目标函数,曲波
变换提供了稳定的、高效的和近乎最优的表示,可以
有效地区分曲线和噪声
[
8-9
]
。本文根据
DPCCT
的
特点,将
犔
1
范数约束和曲波变换系数约束作为约束
条件,结合经典的代数迭代算 法(
ART
)提出了适 用
于相位项 梯 度
δ
重 建 的
ART
犔
1
Curvelet
算 法。
仿真和 实 验 结 果 证 明 了 在 均 方 误 差 意 义 下
ART
犔
1
Curvelet
算法的 重 建 精 度 优 于
ART
和 基 于
犔
1
范数约束 的 代 数 迭 代 算 法 (
ART
犔
1
),能 更 好 地 重
建图像边缘,消除斑点状噪声,在相同的迭代次数下
拥有比
ART
犔
1
算法
[
10
]
更好的重建效果,但曲波变
换消耗 了 大 量 的 时 间,重 建 时 间 大 于
ART
犔
1
算
法。
2
数学物理模型
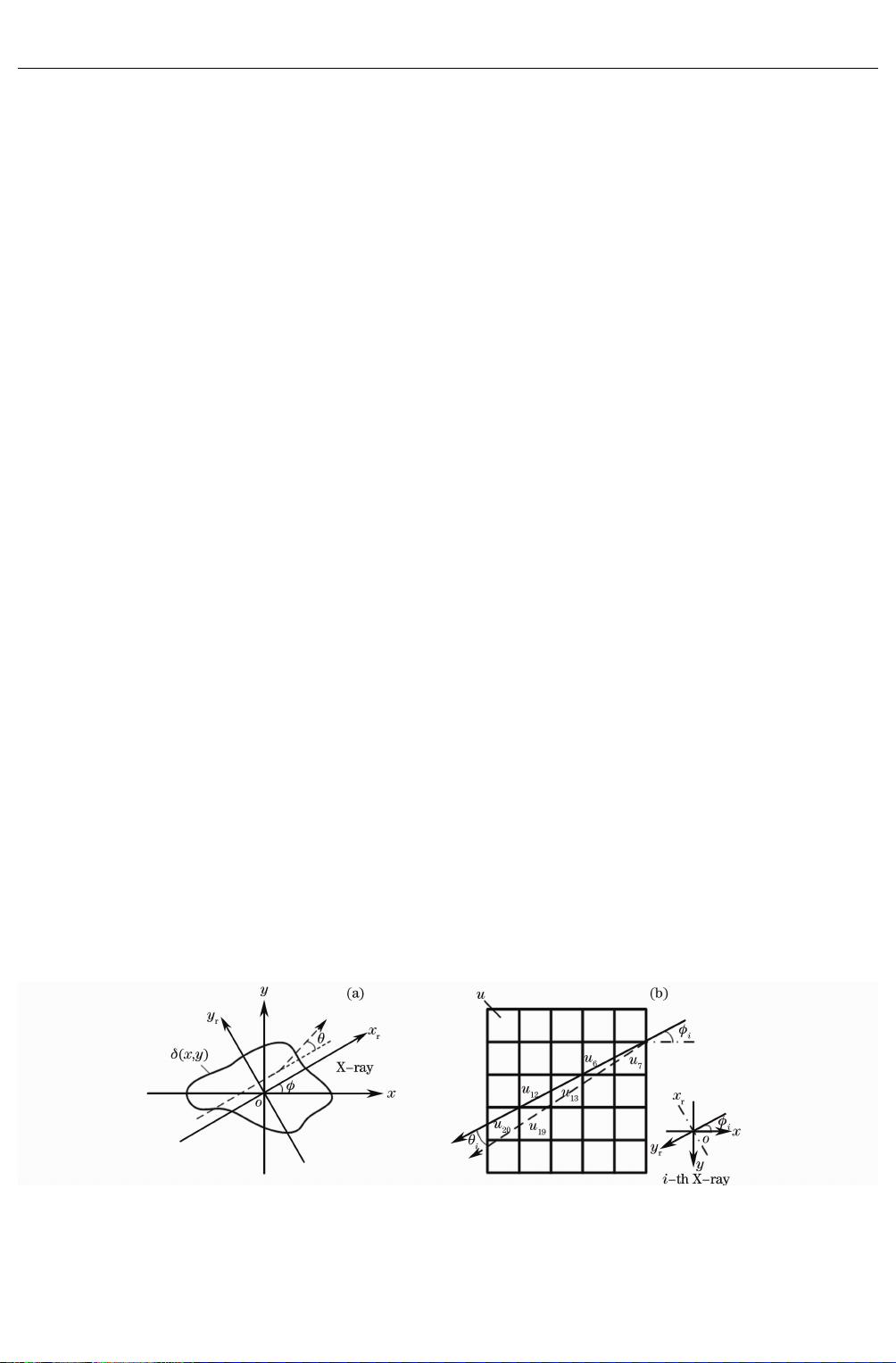
通过二维空间模型来说明微分相位衬度的成像
模型,如图
1
(
a
)所 示。图 中
狓狅
狔
为 固 定 坐 标 系;
狓
r
狅
狔
r
为旋转坐标系;
X
射线的传播方向为
狓
r
轴正
方向;
为射线与
狓
轴正方向的夹角;
θ
为射线穿过物
体后在二维平面内的折射角
;
δ
(
狓
,
狔
)函数代表物体
相位项在二维平面
狓狅
狔
上的分布函数。
图
1
折射作用示意图。(
a
)连续域;(
b
)离散域
Fi
g
.1 Sketchoftherefraction.
(
a
)
Continuousdomain
;(
b
)
discretedomain
物体对
X
射 线 的 折 射 和 吸 收 可 由 复 合 折 射 率
狀
=
1
-
δ
+
i
β
来描述,其中
δ
称为相位项,
β
称为吸收
项。根据 图
1
(
a
)所示的几 何关系,
X
射线经 过物 体
后的折射角
θ
与相位项梯度
δ
的关系可归结为
01110032
剩余11页未读,继续阅读
资源评论

weixin_38732425
- 粉丝: 6
- 资源: 941
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功