python中matplotlib实现最小二乘法拟合的过程详解

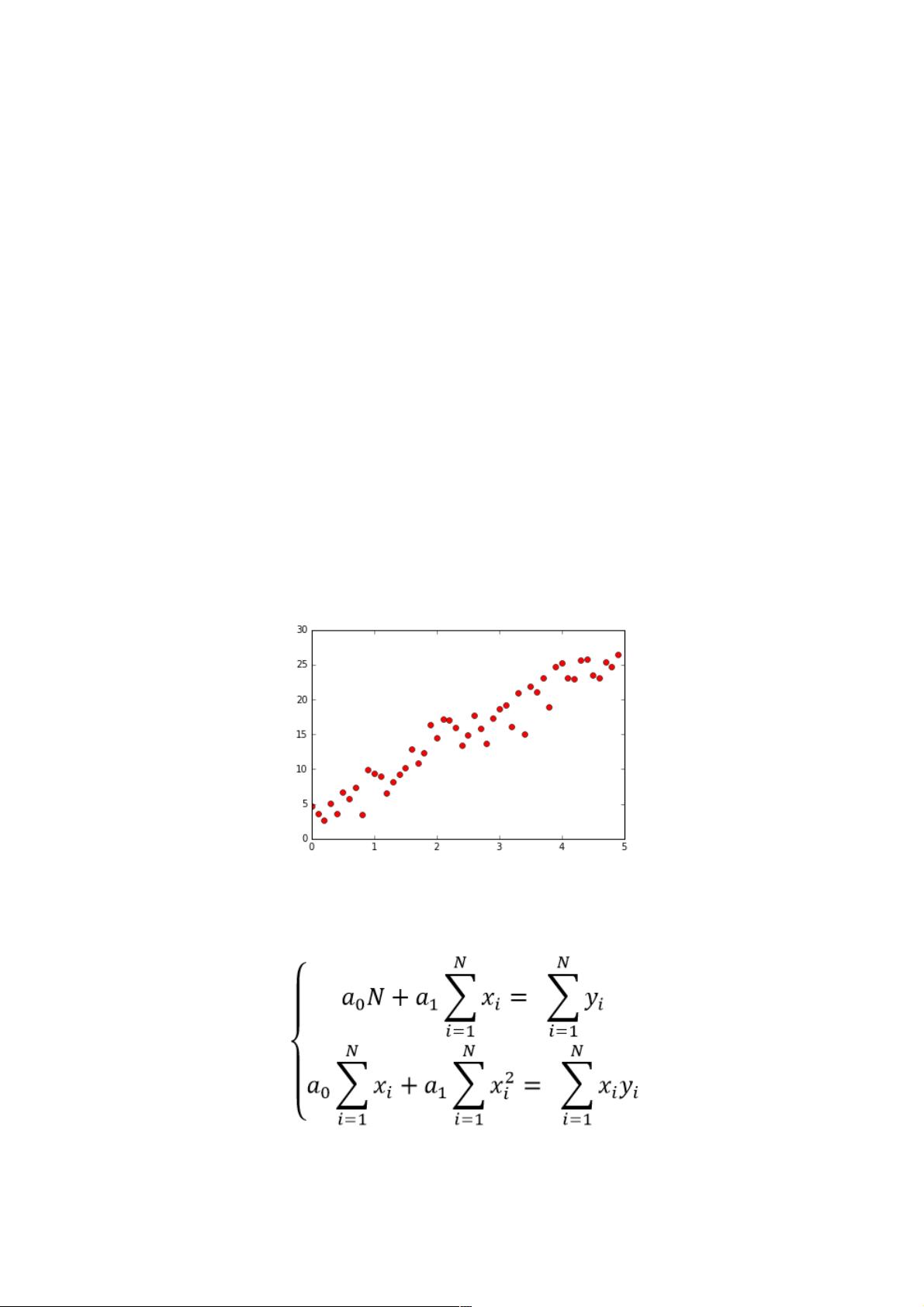
主要给大家介绍了关于python中matplotlib实现最小二乘法拟合的相关资料，文中通过示例代码详细介绍了关于最小二乘法拟合直线和最小二乘法拟合曲线的实现过程，需要的朋友可以参考借鉴，下面来一起看看吧。 ### Python中Matplotlib实现最小二乘法拟合的过程详解 #### 前言 最小二乘法（Least Square Method）是一种广泛应用于统计学、数学、物理学等领域的优化方法，其核心在于通过最小化误差的平方和来寻找数据的最佳函数匹配。这种方法不仅能够有效地求解线性系统中的未知数据，还能应用于非线性系统的参数估计和曲线拟合等问题中。本文将详细介绍如何使用Python编程语言结合Matplotlib库来实现最小二乘法对直线和曲线的拟合。 #### 一、最小二乘法拟合直线 ##### 1.1 生成样本点 为了演示最小二乘法拟合直线的过程，首先我们需要生成一组模拟数据。这里假设有一条直线 \(y = 3 + 5x\)，并在其附近添加一些随机噪声，以模拟真实世界中的数据波动。 ```python import numpy as np import matplotlib.pyplot as plt # 在直线 y = 3 + 5x 附近生成随机点 X = np.arange(0, 5, 0.1) Z = [3 + 5 * x for x in X] Y = [np.random.normal(z, 0.5) for z in Z] plt.plot(X, Y, 'ro') plt.show() ``` 从上述代码中可以看出，我们使用了NumPy库来生成一系列的\(x\)值，并基于这些\(x\)值计算对应的\(y\)值。之后，在每个\(y\)值的基础上添加了一个正态分布的随机噪声，以此来模拟真实的观测数据。最终得到的样本点如图所示。 ##### 1.2 拟合直线 为了拟合一条直线 \(y = a_0 + a_1 * x\)，我们需要使用最小二乘法来求解未知系数\(a_0\)和\(a_1\)。具体可以通过构造一个方程组并利用numpy的`linalg.solve()`函数来解决。 ```python def linear_regression(x, y): N = len(x) sumx = sum(x) sumy = sum(y) sumx2 = sum(x ** 2) sumxy = sum(x * y) A = np.mat([[N, sumx], [sumx, sumx2]]) b = np.array([sumy, sumxy]) return np.linalg.solve(A, b) a0, a1 = linear_regression(X, Y) ``` 通过以上步骤，我们得到了拟合直线的系数\(a_0\)和\(a_1\)。 ##### 1.3 绘制直线 我们将使用Matplotlib来绘制原始样本点以及拟合的直线，并进行对比。 ```python _X = [0, 5] _Y = [a0 + a1 * x for x in _X] plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2) plt.title("y={:.2f}+{:.2f}x".format(a0, a1)) plt.show() ``` #### 二、最小二乘法拟合曲线 ##### 2.1 生成样本点 与拟合直线类似，为了拟合一条曲线 \(y = 2 + 3x + 4x^2\)，我们同样需要生成一组样本点。 ```python # 在曲线 y = 2 + 3x + 4x^2 附近生成随机点 X = np.arange(0, 5, 0.1) Z = [2 + 3 * x + 4 * x**2 for x in X] Y = np.array([np.random.normal(z, 3) for z in Z]) plt.plot(X, Y, 'ro') plt.show() ``` ##### 2.2 拟合曲线 对于一个形如 \(y = a_0 + a_1 * x + a_2 * x^2\) 的二次曲线，我们可以按照类似的步骤来求解未知系数\(a_0\)、\(a_1\)和\(a_2\)。 ```python def gen_coefficient_matrix(X, Y): N = len(X) m = 3 A = [] for i in range(m): a = [] for j in range(m): a.append(sum(X**(i + j))) A.append(a) return A def gen_right_vector(X, Y): N = len(X) m = 3 b = [] for i in range(m): b.append(sum(X**i * Y)) return b A = gen_coefficient_matrix(X, Y) b = gen_right_vector(X, Y) a0, a1, a2 = np.linalg.solve(A, b) ``` ##### 2.3 绘制曲线 与拟合直线一样，我们同样使用Matplotlib来绘制拟合曲线及其与样本点的对比。 ```python _X = np.arange(0, 5, 0.1) _Y = np.array([a0 + a1 * x + a2 * x**2 for x in _X]) plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2) plt.title("y={:.2f}+{:.2f}x+{:.2f}$x^2$".format(a0, a1, a2)) plt.show() ``` ### 结论 本文详细介绍了如何使用Python和Matplotlib来实现最小二乘法对直线和曲线的拟合。通过生成样本点、构造方程组并求解未知系数，最终绘制出拟合的图形。这种方式不仅直观而且实用，适用于多种应用场景，包括但不限于数据分析、预测建模等领域。