没有合适的资源?快使用搜索试试~ 我知道了~
瑞利块衰落信道上多输入多输出混合自动重复请求协议的近似封闭形式功率分配方案
0 下载量 163 浏览量
2021-02-24
19:34:49
上传
评论
收藏 662KB PDF 举报
温馨提示
在这项研究中,解决了在多输入多输出( MIMO )块瑞利衰落信道上的混合自动重发请求( HARQ )协议的停电局限性最佳功率分配问题。 考虑到三种典型的HARQ协议,作者首先推导出MIMO HARQ协议在高信噪比区域的近似中断概率。 然后,基于近似值,他们制定了一个优化问题,即在目标中断概率和最大传输回合次数的约束下,使平均总用电量最小化。 通过解决停电限制的优化问题,可以获得闭合形式的最佳功率序列。 应用这些解决方案,进一步研究了最佳功率序列的单调性。 发现当目标中断概率小于阈值时,最佳功率序列单调增加。 他们还研究了各种条件下系统参数对最佳功率序列和功率分配增益的影响。 最后,给出了数值和仿真结果以验证理论推导。
资源推荐
资源详情
资源评论

Approximate closed-form power allocation
scheme for multiple-input–multiple-output
hybrid automatic repeat request protocols
over Rayleigh block fading channels
ISSN 1751-8628
Received on 29th December 2014
Revised on 9th May 2015
Accepted on 17th July 2015
doi: 10.1049/iet-com.2014.1263
www.ietdl.org
Songhu Ge
✉
, Yong Xi, Shengchun Huang, Yue Ma, Jibo Wei
School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, Hunan, People’s Republic of
China
✉ E-mail: gesonghu@126.com
Abstract: In this study, the outage-limited optimal power allocation problem for hybrid automatic repeat request (HARQ)
protocol over multiple-input–multiple-output (MIMO) block Rayl eigh fading channels is addressed. Considering three
typical HARQ protocols, the authors first derive the approximate outage probabilities of the MIMO HARQ proto cols at
the high signal-to-noise ratio region. On the basis of th e appro ximations, they then formulate an optimisation problem
of minimising the average total power usage with the constraints of the targeted outage probability and the maximum
number of transmission rounds. A closed-form optimal power sequence is obtained by solving the outage-limited
optimisation problem. Applying the solutions, the monotonicity of the optim al power sequence is further investigated.
It is found that the optimal power sequence is monotonically increasing when the targeted outage probability is
smaller than a threshold. They also study the impacts of the system parameter s on the optimal power sequence and
the power allocation gain under various conditions. Finally, the numerical and simulation results are presented to
verify the theoretical derivation.
1 Introduction
As a key technology to improve the spectral efficiency in modern
wireless communications, multiple-input–multiple-output (MIMO)
has been adopted in various communication standards, such as
IEEE 802.11 [1], IEEE 802.16 [2] and 3GPP LTE [3]. On the
other hand, hybrid automatic repeat request (HARQ) protocol [4]
is also the indispensable approach to increase the data transmission
reliability in those standards. Therefore, the HARQ protocols over
MIMO channels are widely studied in the literature to improve the
system performance. By far, the MIMO HARQ related works can
be roughly categorised into three major classes. One class focused
on the performance tradeoff in MIMO HARQ systems. Following
Zheng and Tse’s work in [5], the diversity–multiplexing–delay
tradeoff [6], throughput–diversity–delay tradeoff [7] and rate–
diversity–delay tradeoff [8] for MIMO HARQ were investigated.
The second class studied the system design of MIMO HARQ, for
example, precoder design [9] and detection algorithm design [10].
The last class treated the performance analysis of MIMO HARQ,
for example, outage analysis with multibit feedback [11], transition
control protocol (TCP) performance analysis with packet
combining [12].
Besides those research issues, the energy efficiency is also an
important metric for the HARQ protocols in the energy-limited
networks. Recently, for different kinds of HARQ protocols in
single-input–single-output (SISO) systems, extensive studies have
shown that the power allocation schemes among different
transmission rounds bring significant energy efficiency
improvement. First, for basic HARQ, the optimal power allocation
(OPA) schemes in single- and multi-hop wireless links were
exploited to improve the energy efficiency in [13]. Second, for
chase combining-based HARQ (CC-HARQ), the OPA scheme of
minimising the average total transmission power consumption over
quasi-static Rayleigh fading channels and block Rayleigh fading
channels [In HARQ protocols, the quasi-static fading channel is
commonly defined as the model in which all the transmission
rounds experience the same channel gain, whereas the channel
gains between different transmission rounds are independent for
the block fading channel model.] were investigated in [14, 15],
respectively, while satisfying the given outage probability
constraint. Furthermore, considering the metric of the packet error
rate, Ge et al. [16] further developed a closed-form solution to the
optimisation problem considered in [15
]. At last, for incremental
redundancy HARQ (IR-HARQ), Chaitanya and Larsson [17]
studied the OPA scheme that minimises the packet drop
probability under the average transmit power constraint, and gave
a closed-form solution to the special case of L = 2. Recently in
[18], aiming at minimising the outage-limited average transmission
power, the OPA schemes were obtained under both continuous
and bursting communication models for both CC-HARQ and
IR-HARQ protocols.
Although the power allocation schemes for the HARQ protocols
in SISO systems have been well studied, the results for MIMO
HARQ protocols are limited. Recently in [19], the effects of the
power allocation scheme on the MIMO HARQ system were
discussed and in [20] the energy-limited OPA was studied. It was
shown in [19] that the throughput of the MIMO HARQ system
can be improved by both the temporal power allocation (power
allocation among different transmission rounds) and the spatial
power allocation (power allocation among different antennas), and
it was revealed in [20] that the OPA increases the diversity gain of
the MIMO automatic repeat request (ARQ) remarkably. The
optimisation objects are throughput and outage probability in [19,
20], respectively, instead of the power usage. More importantly,
the solutions of the optimal power sequences were obtained by a
search algorithm in [19] and for the special case of L = 2 in [20],
which are inconvenient to investigate the properties of the optimal
power sequence.
In this paper, we consider the outage-limited OPA problem for
MIMO HARQ protocols over block fading channels, which extend
our prior work in [16] to MIMO systems and three typical HARQ
protocols. Our goal is to find the optimal power sequence that
IET Communications
Research Article
IET Commun., 2015, Vol. 9, Iss. 16, pp. 2023–2032
2023
&
The Institution of Engineering and Technology 2015
minimises the average total power usage under the targeted outage
probability and the maximum number of transmission rounds
constraints for MIMO HARQ protocols. The main contributions of
this paper are summarised as follows. First, we develop the
approximate outage probabilities for three typical MIMO HARQ
protocols at the high signal-to-noise ratio (SNR) region. Second,
using the approximations, the optimisation problem of minimising
the average total power consumption with the targeted outage
probability and the maximum number of transmission rounds
constraints is formulated, and a closed-form solution to the
problem is obtained. Finally, by exploiting the closed-form
solution, we investigate the monotonicity of the optimal power
sequence and derive the necessary conditions for the
monotonically increasing optimal power sequences.
The remainder of this paper is organised as follows. Section 2
presents the system model, HARQ model and the optimisation
problem. Section 3 derives the approximate outage probabilities of
three typical HARQ protocols at the high SNR region. The
closed-form optimal power sequence and its monotonicity are
discussed in Sections 4 and 5, respectively. Then the numerical
and simulation results are provided in Section 6. Conclusions are
given in Section 7.
2 System model and problem formulation
2.1 System model
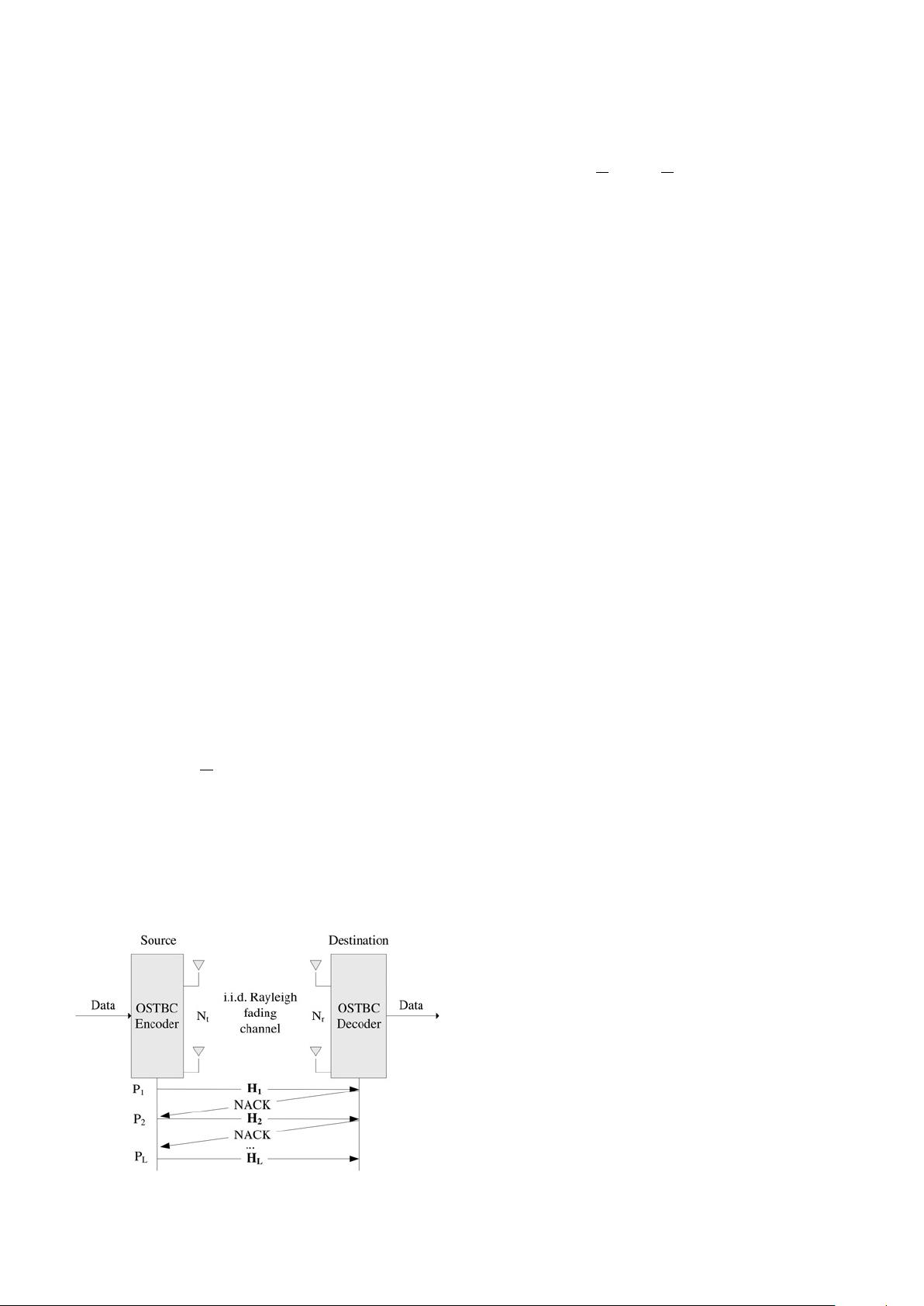
As illustrated in Fig. 1, we consider HARQ protocols over the
MIMO block Rayleigh fading channels with N
t
transmit antennas,
N
r
receive antennas and the maximum number of transmission
rounds L. Let H
l
[ C
N
r
×N
t
,1≤ l ≤ L denote the channel state
matrix at the lth round, which is assumed to be known at the
receiver, but unknown at the transmitter. For block fading
channels, H
l
remains constant during a transmission round, but
changes independently among different transmission rounds.
Moreover, the elements of matrix H
l
, denoted by h
j, k, l
,are
assumed to be independent and identically distributed (i.i.d.)
random variables with mean square magnitude E[|h
j, k, l
|
2
]=1.
Under these assumptions, the signal received at the lth round can
be written as
y
l
=
P
l
N
t
H
l
x + w
l
,1≤ l ≤ L, (1)
where x ∈ C
N
t
×1
is the transmitted signal, P
l
is the transmission
power at the lth round and w
l
∈ C
N
r
×1
is the channel noise vector
at the lth round, whose elements are i.i.d. complex Gaussian
variables with normalised power spectral density N
0
= 1. Let γ
l
,
g
l
be the instantaneous and the average received SNRs at the lth
round, respectively. With an orthogonal space–time block coding
scheme adopted in the MIMO system, the instantaneous SNR at
the lth round can be expressed as
g
l
=
g
l
N
t
H
l
2
F
=
g
l
N
t
N
t
j=1
N
r
k=1
h
j, k, l
2
, (2)
where
g
l
= P
l
/N
0
and ·
2
F
is the Frobenius norm of a matrix.
2.2 HARQ model
Many types of HARQ protocols have been proposed to improve
HARQ efficiency. In this paper, the following three typical HARQ
schemes, which were widely employed in the practice systems and
studied in the literature [18–23], are considered.
† Generalised slotted Aloha (ALO) HARQ protocols: In this
scheme, the protocol works such as in slotted ALO protocols, that
is, the source retransmits the same packet and the destination
attempts decoding the packet using the most recently received
signal in the HARQ process.
† Repetition time diversity (RTD) HARQ protocols: Here, in case of
errors, the source retransmits the same packet and the destination
attempts decoding the packet with the maximum ratio combining
of all the received signals in the previous HARQ rounds. This is
also referred as CC-HARQ [15, 17].
† Incremental redundancy (INR) HARQ protocols: At each HARQ
round, the source sends new redundancy bits and the destination
optimally combines them, and then attempts decoding the packet.
Similarly, this is also referred as IR-HARQ [15, 17].
For simplicity, we assume that the feedback channels are
error-free and delay-free in all protocols. With sufficiently strong
coding and long packet length, the packet loss rate (PLR) can be
well-approximated by the information outage probability for
HARQ protocols [15]. Here, the outage probability is defined as
the probability of the accumulated instantaneous mutual
information after the Lth transmission round smaller than the
targeted spectral efficiency R. For the above three HARQ schemes,
the accumulated instantaneous mutual information at the ith
transmission round is given by [21]
I
i
=
log 1 +
g
i
, ALO
log 1 +
i
l=1
g
l
, RTD
i
l=1
log 1 +
g
l
, INR
⎧
⎪
⎨
⎪
⎩
(3)
2.3 Optimisation problem formulation
Here, we consider the optimisation problem of minimising the
average power usage
P with the targeted PLR (or equivalently the
outage probability) constraint p
0
by finding the optimal
transmission power sequence P =[P
1
, P
2
, …, P
L
]. Given the
outage probability after L transmission rounds p
out
(L), the
outage-limited optimisation problem can be formulated as
min
P with respect to P
s.t. p
out
L()≤p
0
.
(4)
As formulated in [14, 15], the average power usage can be calculated
as follows
P = P
1
+
L
l=2
P
l
p
out
l − 1(), (5)
where p
out
(i) is the outage probability after the ith round. To solve
the optimisation problem in (5), the outage probability p
out
(i)is
indispensable. However, the exact outage probability expressions
Fig. 1 System model
IET Commun., 2015, Vol. 9, Iss. 16, pp. 2023–2032
2024
&
The Institution of Engineering and Technology 2015
剩余9页未读,继续阅读
资源评论

weixin_38724106
- 粉丝: 3
- 资源: 911
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功