线性规划单纯形法、大M法,非线性规划的拉格朗日乘子法的手推法,excel、python编程以及python包编程
线性规划单纯形法、大M法,非线性规划的拉格朗日乘子法的手推法,excel、python编程以及python包编程 目录(1) 线性规划单纯形法概念定义标准形式步骤大M法概念定义步骤EXCEL求解单纯形法大M法Python编程Python包编程(2)非线性规划非线性规划的拉格朗日乘子法的Excel,python编码和python包编码等式约束的拉格朗日乘子法不等式约束的拉格朗日乘子法无约束的拉格朗日乘子法(KKT条件下)手推法python包编程参考文献 (1) 线性规划 单纯形法概念 定义 一般线性规划问题中当线性方程组的变量数大于方程个数,这时会有不定数量的解,而单纯形法是求解线性规划问题的 线性规划是一种优化方法,用于在满足一组线性约束的情况下最大化或最小化一个线性目标函数。单纯形法是解决线性规划问题的最常用算法,由美国数学家乔治·丹齐克在1947年提出。这种方法适用于变量数量多于方程数量的情况,即存在多个可能解的情况。单纯形法的核心思想是通过迭代过程,每次选取一个更优的基础解,直至找到目标函数的最大值或最小值。 单纯形法的操作步骤如下: 1. 将线性规划问题转换为标准形式,即目标函数为最大化,所有变量非负,约束条件为等式。 2. 初始化一个基础解,通常是通过大M法或两个非负解来实现。大M法是通过引入人工变量和一个非常大的正数M,使不等式约束转化为等式,然后通过单纯形法找到初始基础解。 3. 构建初始单纯形表,包含当前基础解的系数、目标函数系数、检验数等。 4. 检查当前基础解是否是最优解,如果不是,找到一个能提高目标函数值的非基变量,替换掉一个基变量,并更新单纯形表。 5. 重复步骤4,直至所有非基变量的检验数都小于等于零,表明找到了最优解。 对于非线性规划问题,拉格朗日乘子法是一种有效的求解工具。拉格朗日乘子法引入拉格朗日函数,结合等式和不等式约束,通过求解拉格朗日方程来寻找可能的解。对于有等式约束的非线性规划,拉格朗日乘子直接应用于约束条件;对于不等式约束,可以通过引入松弛变量和大M法转化为等式约束;无约束的非线性规划,可以通过KKT(Karush-Kuhn-Tucker)条件来确定最优解。 在实际操作中,Excel和Python都可以用于线性和非线性规划的求解。Excel提供了内置的线性规划求解器,用户只需输入目标函数和约束条件,即可得到解。Python则可以利用优化库如`scipy.optimize`的`linprog`函数解决线性规划问题,对于非线性规划,可以使用`scipy.optimize.minimize`函数配合拉格朗日乘子法的实现。此外,还有专门的Python包如`cvxopt`和`pulp`,它们提供了更高级的接口来处理线性和非线性规划问题。 在编程实现时,需要理解每一步骤的数学原理,并能够将这些原理转化为代码。这不仅要求掌握基本的编程技能,还需要熟悉优化理论和数值计算方法。通过Excel和Python的编程实践,不仅可以加深对线性和非线性规划算法的理解,还能提高问题解决能力。

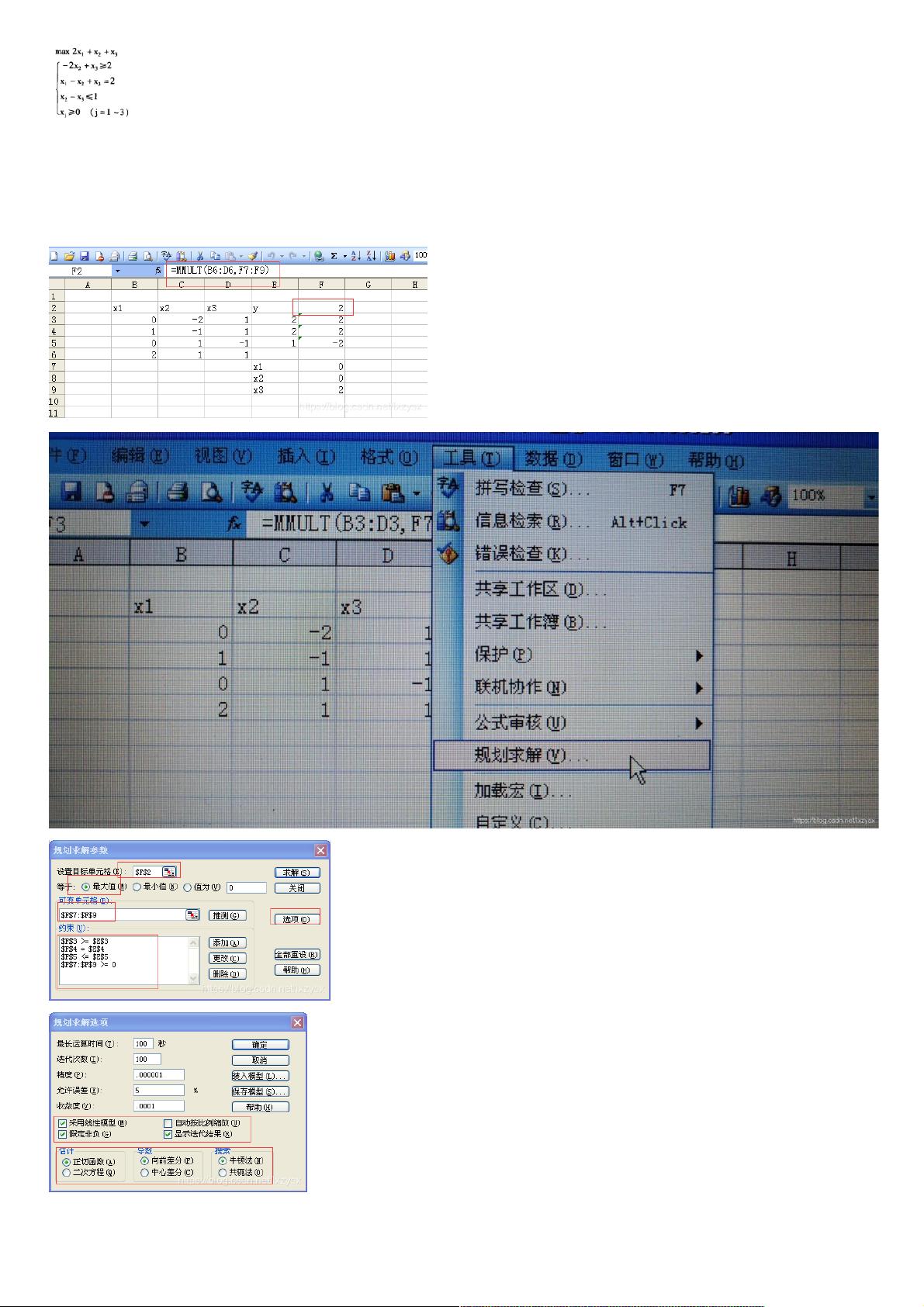
剩余7页未读,继续阅读
- 粉丝: 4
- 资源: 991
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0