基于忆阻电子突触的新型Hermite混沌神经网络及其在密码学中的应用资源-CSDN文库

Hermite

neural

171 浏览量 2021-02-25 10:27:38 上传评论收藏 954KB PDF 举报

资源推荐

资源详情

资源评论

A novel memristive electronic synapse-based Hermite chaotic neural

network with application in cryptography

Xinli Shi

, Shukai Duan

, Lidan Wang

, Tingwen Huang

, Chuandong Li

School of Electronic and Information Engineering, Southwest University, Chongqing, China

Department of Electrical and Computer Engineering Texas A&M University, Doha, Qatar

article info

Article history:

Received 10 August 2014

Received in revised form

30 October 2014

Accepted 5 March 2015

Communicated by He Huang

Available online 28 April 2015

Keywords:

Hermite neural network

Memristor

Chaotic

Encryption

Decryption

abstract

The memristor is a kind of non-linear passive two-terminal electrical device, which is widely applied in

neural networks currently. In this paper, a new synaptic weight update learning rule of Hermite neural

network is proposed by combining Hermite polynomials with memristors to build a memristive Hermite

chaotic neural network (MHCNN). The chaotic series is generated by the weights of the neural network

and chaotic initial value. And ultimately we can obtain the ciphertext by encrypting the plaintext. The

use of memristors results in a very special neural network, which can not only change the polynomial in

neural network but also achieve the diversity, and the conﬁdentiality of communication is also improved

effectively.

1. Introduction

The concept of memristor was initially proposed by Chua in

1 971 [1]. However, it is until the year of 2008 that HP Lab declared

the physical realization of the memristor [2–4]. Since then, wide

attention around the world was put on this newly-found element.

Several years' researches have witnessed the proposals of a

number of new memristor models [5–13]. Because of its unique

switch mechanism, natural memory function, continuous input

and output characteristics and nanoscale size, the memristor has

shown great potential in nonvolatile memory, artiﬁcial neural

networks and intelligent information etc. and aroused lots of

studies in these ﬁelds [14–22]. For example, Aﬁﬁ et al. studied

the realization of STDP learning rules based on the pulsing

neuromorphic networks with memristor cross-array [14]. Sangho

et al. demonstrated that memristors can be used to implement

programmable analog circuits, leveraging memristor's ﬁne-

resolution programmable resistance without causing perturba-

tions due to the parasitic components [15]. Duan et al. proposed

memristor-based resistive random access memory (MRRAM) and

veriﬁed its effectiveness in storing ASCII characters and gray-scale

images in binary format [16]. Duan et al. also studied chaotic

circuity [17,27–31] and memristor-based cellular nonlinear/neural

network [18]. Wang et al. maked important studies of memristor

model and chaos generation [19]. Among all the memristor's

properties shown before, the uniqueness of nanoscale size has

attracted much attention and interests. Because of that character-

istic, a small voltage through it will cause strong change in electric

ﬁeld and then lead to nonlinear ionic drift, which brings about the

proposal of nonlinear memristor models and related research.

As is known, the applications of digital information have made

great contribution to the rapid development of modern technology

and network. The process of gaining information becomes simpler

and easier, however, the secrecy of communication calls forth the

researchers' attention gradually. In secret communication, crypto-

graphy is one of the basic methods, which is about the practice

and study of techniques for secure communication in the presence

of third parties, in other words, it is about constructing and

analyzing protocols that will overcome the inﬂuence of adver-

saries and are related to various aspects in information security,

such as data conﬁdentiality, data integrity, authentication and

non-repudiation. Meanwhile, chaos, with the special superiority in

secure communication, is a seemly irregular inner random motion

in a deterministic system and a chaotic system has the properties

of complex pseudo-randomness and extreme sensitivity to initial

values, therefore it is reasonable to incorporate the conception of

chaotic system into communication encryption. Some valuable

work has been done [23–26]. In 1990, Carroll ﬁrstly built a

synchronous chaotic circuit [23]. Several years later, Milanovic

proposed the synchronization of chaotic neural networks [24].

Contents lists available at ScienceDirect

journal h omepage: www.else vier.com/locate/neu com

Neurocomputing

http://dx.doi.org/10.1016/j.neucom.2015.03.018

Corresponding author.

E-mail address: duansk@swu.edu.cn (S. Duan).

Neurocomputing 166 (2015) 487–495

After that, scholars started to apply the chaotic series to cryptology

with great enthusiasm. Their research shows that chaotic syn-

chronization encryption algorithm requires keeping highly con-

sistent between the sender and the receiver, otherwise, several

problems will be produced, such as parameters' mismatching,

inconformity between sent time and received time etc., which

makes the scholars embark on the study of asynchronous encryp-

tion algorithm.

This paper realizes the Hermite neural network's synaptic

weight update by memristors and obtains a special neural net-

work, which not only changes the polynomial in neural network

but also achieves diversity. Speciﬁcally, we trained the memristive

Hermite neural network (MHNN) by using Logistic chaotic series

and obtained memristive Hermite chaotic neural network

(MHCNN), whose structure is special and meets the requirements

of encryption, for the receiver to decrypt the plaintext asynchro-

nously. It must be stated here that encryption and decryption in

this paper use the same network which must be sent secretly.

Moreover, both the cross-correlation function values between

different chaos initial values tend to be zero and the entirely

different ciphertexts improve the security of communication.

The rest of the paper is organized as follows. In Section 2, the

nonlinear memristor model is introduced. The relationships

between the main variables are given by numerical simulation.

The changed rate of memristive conductance is described as the

synapse weight update rule based on theoretical derivation. In

Section 3, memristive Hermite neural network and learning

algorithm are described. Section 4 gets a MHCNN by using a

chaotic series to train the proposed MHNN. Then the MHCNN is

applied to encrypt one paragraph of secretary-general's message

on World Water Day in 2013. Section 5 uses another memristor

model with forgetting effects to build a memristive Hermite neural

network, which is applied to encrypt the same plaintext. The

results under different memristor models are compared. Finally,

the conclusions are given in Section 6.

2. The memristive electronic synapse

The physical model of the memristor consists of a two-layer

thin ﬁlm of TiO

sandwiched between two platinum electrodes.

One of the layers is a thin ﬁlm of TiO

which is doped with oxygen

vacancies. It is described as TiO

2x

and called as doped layer. The

other layer is described as TiO

, which is a pure thin ﬁlm of TiO

and called as undoped layer. Generally, an external excitation v(t)

applied across the memristor may cause oxygen vacancies drift

under the action of electric ﬁeld and the boundary between the

two regions would be moved correspondingly with the total

memristance changed eventually.

The resistance of the memristor can be calculated [21]

M ðtÞ¼R

ω tðÞ



þR

of f

1

ω tðÞ



ð1Þ

When ω¼D or ω¼0,thememristanceequalsR

or R

off

respec-

tivel y . Setting x ¼ðω=DÞA 0; 1

½

, (1) can be described as follows:

MtðÞ¼R

of f

þ R

R

of f



xtðÞ ð2Þ

M 0ðÞ¼R

of f

þ R

R

of f



; when t ¼ 0: ð3Þ

The movement rate of boundary between doped and undoped

regions

¼ ki tðÞfxðÞ; k ¼

: ð4Þ

The a verag e ionic mobility is μ

E 10

14

1

. Real mem-

ristor is a nanoscale device, and enormous electric ﬁelds will be

produced when it is applied with a small voltage. And it can produce

signiﬁcant nonlinearities in the ionic transport, so a pr oper window

function f(x)ontherightsideofEq.(4) is mult iplied to simulate the

nonlinear ionic drift. In general, classic window functions include

Joglekar window function and Biolek window function. Here, we

choose Joglekar window function, which can be described as

fxðÞ¼1 2x1ðÞ

where p is a positi ve integer. The relationships between the memris-

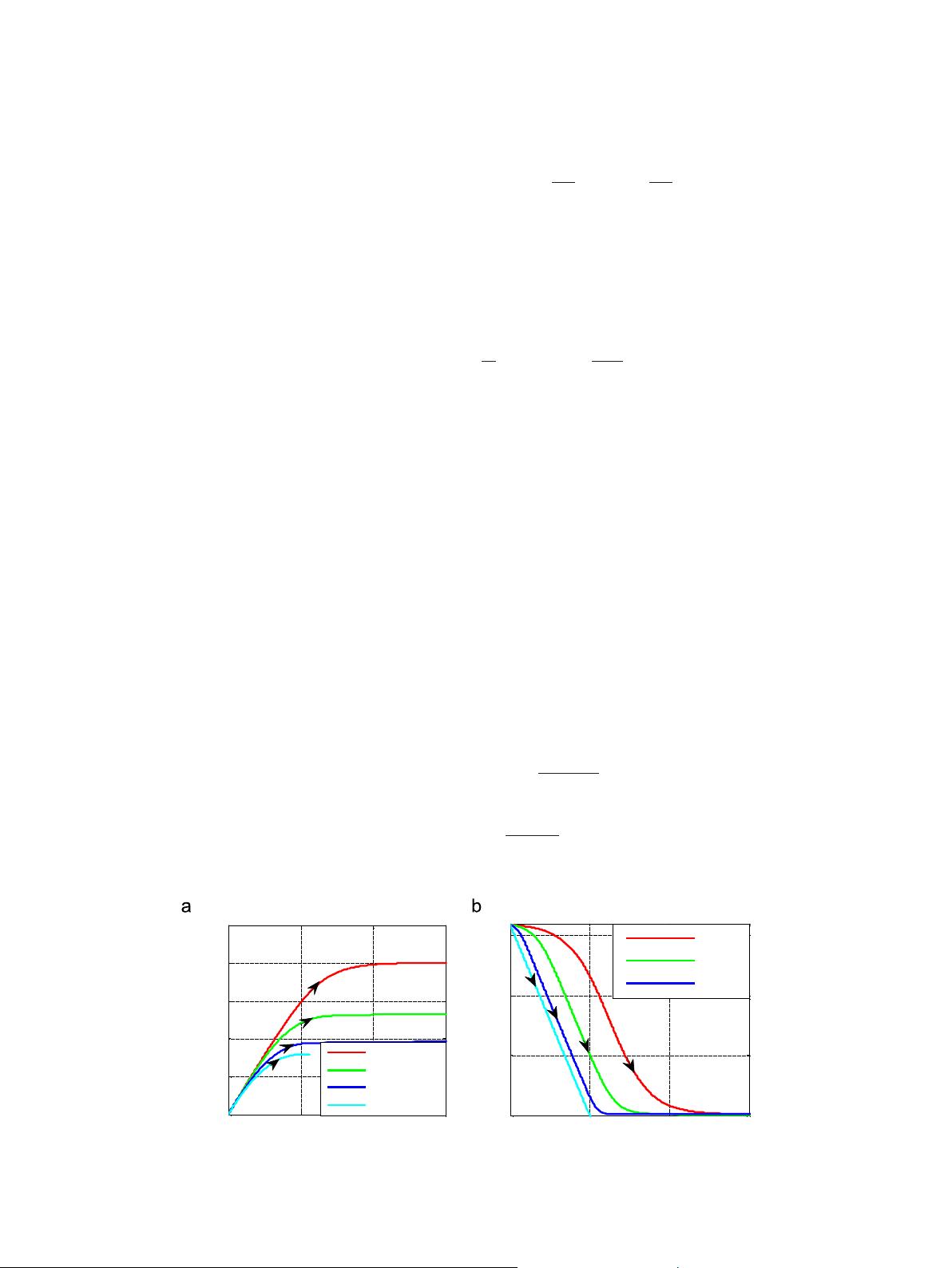
tor's main variables vary with the change of parameter p,whichare

exhibited in Fig. 1.

The memristor model tends to be linear as the value of parameter

p becomes bigger. The nonlinearity of a memristor becomes the most

obvious when p¼ 1, which simulat es the nonlinear beha viors of

memristors better than other values. So we choose the window

function of p¼1.

fxðÞ¼4x 4x

ð5Þ

Substitute Eq. (5) into Eq. (4), and assume that there is no input

when t¼0, q

¼0. Finally, x(t) can be described by

xtðÞ¼1

4kq tðÞ

þ1

ð6Þ

where

A ¼

of f

R

: ð7Þ

0 1 2 3

x 10

-4

0.5

1.5

2.5

Charge ( c )

Flux ( Wb )

p=1

p=2

p=5

Linear Model

0 1 2 3

x 10

-4

Charge ( c )

Memristance ( K

)

p=1

p=2

p=5

Fig. 1. (a) Relationships between the charge and the ﬂux for different values of parameter p. (b) Relationships between the charge and the memristance for different values

of parameter p.

X. Shi et al. / Neurocomputing 166 (2015) 487–495488

剩余8页未读，继续阅读

评论收藏

内容反馈

weixin_38719643

粉丝: 7
资源: 941

基于忆阻电子突触的新型Hermite混沌神经网络及其在密码学中的应用

基于MNIST的忆阻神经网络稳定性研究

基于STDP 规则和忆阻桥突触的神经网络及图像处理

基于基于忆阻器的联想记忆神经网络的情感建模

双极性脉冲忆阻桥电子突触神经网络及图像处理

09 忆阻突触耦合Hopfield神经网络的初值敏感动力学.pdf

基于忆阻器的神经网络应用研究.pdf

基于忆阻脉冲耦合神经网络的图像去噪.pdf

忆阻在神经网络中的应用.pdf

基于忆阻神经网络的车辆标志识别技术研究.pdf

基于忆阻神经网络的锂电池SOC检测技术研究.pdf

01 基于忆阻器的混沌、存储器及神经网络电路研究进展.pdf

基于忆阻的时变时滞神经网络的自适应同步.pdf

基于忆阻器的连续学习混沌神经网络

网络游戏-基于忆阻器件的神经网络突触结构及突触权重构建方法.zip

一种新的有源忆阻器在耦合FHN神经网络中的应用.pdf

忆阻突触耦合Hopfield神经网络的初值敏感动力学.pdf

基于新型忆阻器突触的多步量化尖峰时间依赖型塑形人工神经元设计

容忍忆阻器非理想特性的深层神经网络算法研究.pdf

基于忆阻神经网络的光伏面板清扫机器人PID控制器研究.pdf

局部有源忆阻器电路及其在HR耦合神经元网络中的应用.docx

基于忆阻器交叉构架的同步神经网络系统

一种基于忆阻特性的监督神经网络算法及电路设计.pdf

一种基于忆阻器的用于识别手写数字图像神经网络研究.pdf

忆阻神经网络实验的数值实验代码

Hopfield_my_1pic_1pic一图_基于忆阻器的车标识别_神经网络_忆阻神经网络_忆阻器_

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）