没有合适的资源?快使用搜索试试~ 我知道了~
Continuous-variable measurement-device-independent quantum key d...
1 下载量 14 浏览量
2021-02-21
01:28:23
上传
评论
收藏 842KB PDF 举报
温馨提示
We propose a continuous-variable measurement-device-independent quantum key distribution (CV-MDI QKD) protocol, in which detection is conducted by an untrusted third party. Our protocol can defend all detector side channels, which seriously threaten the security of a practical CV QKD system. Its security analysis against arbitrary collective attacks is derived based on the fact that the entanglement-based scheme of CV-MDI QKD is equivalent to the conventional CV QKD with coherent states and hete
资源推荐
资源详情
资源评论

PHYSICAL REVIEW A 89, 052301 (2014)
Continuous-variable measurement-device-independent quantum key distribution
Zhengyu Li,
1,2
Yi-Chen Zhang,
3
Feihu Xu,
4
Xiang Peng,
1,*
and Hong Guo
1,2,†
1
State Key Laboratory of Advanced Optical Communication Systems and Networks, School of Electronics Engineering and Computer Science
and Center for Quantum Information Technology, Peking University, Beijing 100871, China
2
Center for Computational Science and Engineering, Peking University, Beijing 100871, China
3
State Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications,
Beijing 100876, China
4
Centre for Quantum Information and Quantum Control, Department of Physics and Department of Electrical and Computer Engineering,
University of Toronto, Toronto, Ontario, Canada M5S 3G4
(Received 23 December 2013; published 7 May 2014)
We propose a continuous-variable measurement-device-independent quantum key distribution (CV-MDI QKD)
protocol, in which detection is conducted by an untrusted third party. Our protocol can defend all detector side
channels, which seriously threaten the security of a practical CV QKD system. Its security analysis against
arbitrary collective attacks is derived based on the fact that the entanglement-based scheme of CV-MDI QKD is
equivalent to the conventional CV QKD with coherent states and heterodyne detection. We find that the maximal
total transmission distance is achieved by setting the untrusted third party close to one of the legitimate users.
Furthermore, an alternate detection scheme, a special application of CV-MDI QKD, is proposed to enhance the
security of the standard CV QKD system.
DOI: 10.1103/PhysRevA.89.052301 PACS number(s): 03.67.Dd, 03.67.Hk
I. INTRODUCTION
Quantum key distribution (QKD) [1,2] can establish a
secure key between two legitimate partners (Alice and Bob)
through insecure quantum and classical channels. In recent
decades research on QKD has evolved rapidly. Some commer-
cial systems are available in the market now [3]. QKD has two
main approaches: one is discrete-variable (DV) QKD, and the
alternative is continuous-variable (CV) QKD [4–6]. CV QKD
has the advantage of being compatible with standard telecom-
munication technology, especially no request on single-photon
detectors. A Gaussian-modulated CV QKD protocol using
coherent states [7,8] has been proved to be secure against
arbitrary collective attacks [9,10], which is optimal in both
the asymptotic case [11] and the finite-size regime [12,13].
A recent experiment has successfully distributed secure keys
over an 80-km optical fiber [14], showing the potential of
long-distance communication using CV QKD protocols.
Generally speaking, the theoretical security analysis of
QKD relies on some ideal theoretical models. However,
the practical devices often have some imperfections and
deviate from the theoretical models. Thus the mismatch
between practical devices and their idealized models may
open security loopholes, which make the practical systems
vulnerable to attacks [15]. In DV QKD systems, various types
of attacks against imperfect devices were proposed, among
which the attacks against the single-photon detector are the
most significant ones [16–18]. Recently in CV QKD systems,
several attack strategies against practical detectors were also
proposed [19–24]. For example, the calibration attack [20] and
local oscillator (LO) fluctuation attack [21] take advantage of
modifying LO to manipulate the measurement results, which
will make Alice and Bob overestimate the secret key rate. The
*
Corresponding author: xiangpeng@pku.edu.cn.
†
Corresponding author: hongguo@pku.edu.cn.
wavelength attack [22,23] allows the eavesdropper to launch an
intercept-resend attack because of the wavelength-dependent
property of the fiber beam splitter used in the heterodyne
detector. The saturation attack [24] can force Alice and Bob
to underestimate the excess noise by saturating the homodyne
detector, which can hide the presence of an intercept-resend
attack.
A natural attempt to remove these attacks in a CV QKD
system was to characterize the specific loophole and find
a countermeasure. For instance, Jouguet et al. proposed an
efficient countermeasure against the calibration attack by
monitoring the LO [20]. Once an attack is known, prevention is
usually simple. However, it is difficult to fully characterize real
detectors and account for all loopholes. Therefore figuring out
how to defend against general attacks on detectors in practical
systems becomes critical in CV QKD.
Inspired by the novel detector-attack-immune protocols,
i.e., measurement-device-independent (MDI) QKD proto-
cols [25–27], which were well analyzed in theory [28–31]
and successfully demonstrated in experiments [32–35], here
we propose a CV-MDI QKD protocol which can also defend
all detector side channels. The main idea is that both Alice and
Bob are senders and an untrusted third party, named Charlie,
is introduced to realize the measurement. Such measurement
results will be used by Alice and Bob in the postprocessing
step to generate secure keys.
By introducing the equivalent entanglement-based (EB)
scheme of this protocol, we show the security analysis against
arbitrary collective attacks, which is based on the fact that the
entanglement-based scheme of CV-MDI QKD is equivalent
to the CV QKD with coherent states and heterodyne detec-
tion [8]. A corresponding prepare-and-measure (PM) scheme
is proposed for implementation. Moreover, the performance
of our protocol against collective entangling cloner attack
is presented via numerical simulations. When the distance
between Alice and Charlie equals that between Bob and
Charlie (symmetric case), the transmission distance is below
1050-2947/2014/89(5)/052301(8) 052301-1 ©2014 American Physical Society
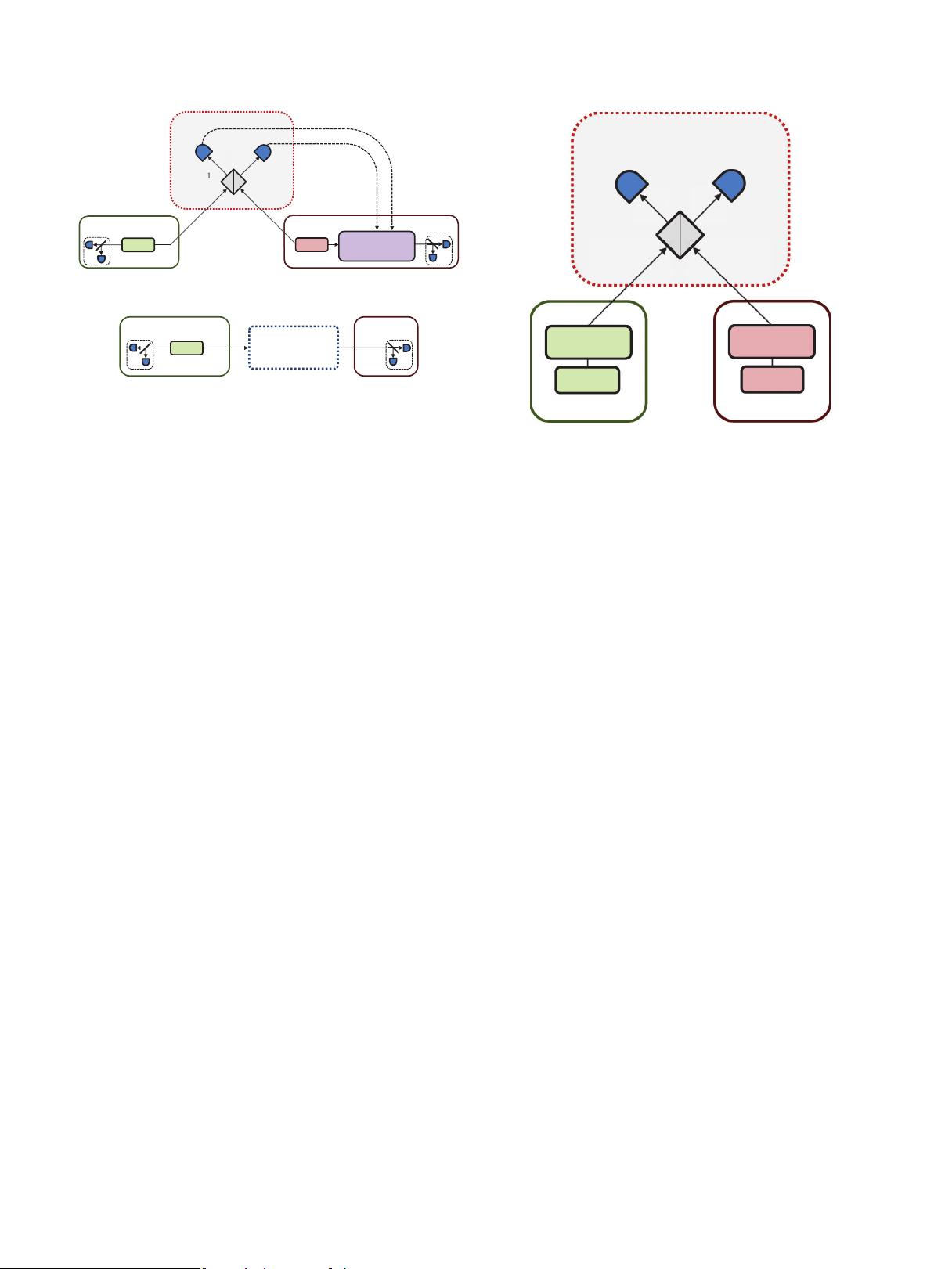
LI, ZHANG, XU, PENG, AND GUO PHYSICAL REVIEW A 89, 052301 (2014)
Het
BS
Hom
1x
C D
A'
Alice
Bob
D
m
1
x
C
Charlie
Het
X
C
P
D
= g (X
C
+ i P
D
)
A
1
Bob
Alice
Channel
(b)
(a)
L
AC
EPR EPR
Displacement:
D( )
EPR
A
2
L
BC
B'
Hom
2p
B
2
B
1
B
1
'
Het
A
1
B
1
'
Het
Β
Β
FIG. 1. (Color online) (a) EB scheme of the CV-MDI QKD
protocol. EPR: two-mode squeezed state. Het: heterodyne detection.
Hom
1x
: homodyne detection of measuring the x quadrature. Hom
2p
:
homodyne detection of measuring the p quadrature. X
C
,P
D
: mea-
surement results of Hom
1x
and Hom
2p
, respectively. BS: 50:50 beam
splitter. (b) Equivalent one-way model of the EB scheme under the
assumptions that Eve controls channels, Charlie and Bob’s EPR state,
and the displacement in (a).
10 km. However, in the asymmetric case the transmission
distance can be improved, reaching 80 km under certain
conditions. This demonstrates the feasibility of our scheme.
This paper is organized as follows: In Sec. II, the detailed
descriptions of both the EB and PM schemes of CV-MDI
QKD are given. In Sec. III, we present the security analysis
for the CV-MDI QKD protocol. In Sec. IV, we show the
numerical simulation results of the secret key rate and discuss
the performance and potential applications.
II. CONTINUOUS-VARIABLE
MEASUREMENT-DEVICE-INDEPENDENT
QKD PROTOCOL
In the PM scheme of a standard QKD protocol such as
Bennett-Brassard 1984 (BB84) [36], Alice randomly prepares
an encoded quantum state and sends it to Bob for detection.
This PM scheme can be formulated in an EB version of the
protocol as follows: Alice first creates an entangled state such
as a Bell state, and afterwards, she measures one mode of this
entangled state in a certain basis, thereby producing the correct
state f or the other mode that is sent to Bob.
In practice, the PM scheme is usually easy to apply,
while the equivalent EB scheme is convenient for security
analysis. The EB scheme of DV-MDI QKD can be seen
as a one-way protocol using entanglement swapping as an
untrusted quantum relay [25,26]. Here we use the same idea
in our CV-MDI QKD protocol, which exploits the continuous-
variable entanglement swapping [37,38]. The EB scheme of
the CV-MDI QKD protocol shown in Fig. 1(a) is described as
follows.
Step 1. Alice generates one two-mode squeezed (TMS) state
and keeps mode A
1
while sending the other mode, A
2
,toan
untrusted third party (Charlie) through the channel with length
L
AC
. Bob generates another TMS state and keeps the mode B
1
Charlie
Bob
Laser
Gaussian
Modulation
Alice
Laser
Gaussian
Modulation
BS
Hom
1x
'
'
Hom
2p
A
B
S
'
B
B
'
C
D
A
B
FIG. 2. (Color online) PM scheme of CV-MDI QKD. Hom
1x
:
homodyne detection of measuring the x quadrature. Hom
2p
: ho-
modyne detection of measuring the p quadrature. BS: 50:50 beam
splitter.
while sending the other mode, B
2
, to Charlie through another
channel with length L
BC
.
Step 2. Modes A
and B
received by Charlie interfere at a
beam splitter (BS) with two output modes C and D. Then both
the x quadrature of C and p quadrature of D are measured by
homodyne detections, and the measurement results {X
C
,P
D
}
are publicly announced by Charlie.
Step 3. After receiving Charlie’s measurement results,
Bob displaces mode B
1
by operation
ˆ
D(β) and gets ˆρ
B
1
=
ˆ
D(β)ˆρ
B
1
ˆ
D
†
(β), where ˆρ
X
represents the density matrix of
mode X, β = g(X
C
+ iP
D
), and g represents the gain of the
displacement. Then Bob measures mode B
1
to get the final data
{X
B
,P
B
}using heterodyne detection. Alice measures mode A
1
to get the final data {X
A
,P
A
} using heterodyne detection.
Step 4. Alice and Bob use an authenticated public channel
to finish the parameter estimation, information reconciliation,
and privacy amplification steps.
After Charlie’s measurements and Bob’s displacement,
mode A
1
and mode B
1
become entangled [37]. Therefore,
after both Alice’s and Bob’s heterodyne detections, their final
data are correlated. The equivalent PM scheme is shown in
Fig. 2, which is described as follows.
Step 1. Alice randomly prepares a coherent state
|x
A
+ ip
A
, where x
A
and p
A
are Gaussian distributed with
variance V
A
− 1. Bob randomly prepares another coherent
state |x
B
+ ip
B
, where x
B
and p
B
are Gaussian distributed
with variance V
B
− 1. Both Alice and Bob send their coherent
states to Charlie through two different channels.
Step 2. The two modes (A
and B
) received by Charlie
interfere at a BS with two output modes C and D. Then both
the x quadrature of C and p quadrature of D are measured by
homodyne detections, and the measurement results {X
C
,P
D
}
are publicly announced by Charlie.
Step 3. When Alice and Bob receive Charlie’s measurement
results, Bob modifies his data as X
B
= x
B
+ kX
C
,P
B
= p
B
−
kP
D
, while Alice keeps hers unchanged, X
A
= x
A
,P
A
= p
A
.
052301-2
剩余7页未读,继续阅读
资源评论

weixin_38719643
- 粉丝: 7
- 资源: 941
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功