没有合适的资源？快使用搜索试试~ 我知道了~

文库首页开发技术其它DataMining-ch6-计算机科学

DataMining-ch6-计算机科学

Papers

Specs

Decks

Manuals

0 下载量 63 浏览量 2021-04-22 18:31:02 上传评论收藏 19.36MB PDF 举报

温馨提示

试读

71页

Chapter 6: Probability and Naive BayesNaïve BayesLet us return yet again to our women athlete example. Suppose I ask you what sport Brittney Griner participates in (gymnastics, marathon running, or basketball) and I tell you she is 6 foot 8 inches and weighs 207 pounds. I imagine you would say basketball and if I ask you how confident you feel about your decision I imagine you would say something along the lines of “pretty darn confident.”Now I ask you what sport Heather Zurich (pictured

资源推荐

资源详情

资源评论

Chapter 6: Probability and Naive Bayes

Naïve Bayes

Let us return yet again to our women athlete example. Suppose I ask you what sport Brittney

Griner participates in (gymnastics, marathon running, or basketball) and I tell you she is 6

foot 8 inches and weighs 207 pounds. I imagine you would say basketball and if I ask you

how confident you feel about your decision I imagine you would say something along the

lines of “pretty darn confident.”

Now I ask you what sport Heather Zurich (pictured

on the right) plays. She is 6 foot 1 and weighs 176

pounds. Here I am less certain how how will answer.

You might say ‘basketball’ and I ask you how

confident you are about your prediction. You

probably are less confident than you were about your

prediction for Brittney Griner. She could be a tall

marathon runner.

Finally, I ask you about what sport Yumiko Hara

participates in; she is 5 foot 4 inches tall and weighs

95 pounds. Let's say you say ‘gymnastics’ and I ask

how confident you feel about your decision. You will

probably say something along the lines of “not too

confident.” A number of marathon runner have

similar heights and weights.

With the nearest neighbor algorithms, it is difficult to

quantify confidence about a classification. With

classification methods based on probability—

Bayesian methods—we can not only make a classification but we can make probabilistic

classifications—this athlete is 80% likely to be a basketball player, this patient has a 40%

chance of getting diabetes in the next five years, the probability of rain in Las Cruces in the

next 24 hours is 10%.

Nearest Neighbor approaches are called

lazy learners. They are called this

because when we give them a set of

training data, they just basically save—

or remember—the set. Each time it

classifies an instance, it goes through

the entire training dataset. If we have

a 100,000 music tracks in our

training data, it goes through the

entire 100,000 tracks each time it

classifies an instance.

Bayesian methods are called eager

learners. When given a training set

eager learners immediately analyze the

data and build a model. When it wants

to classify an instance it uses this

internal model. Eager learners tend to

classify instances faster than lazy

learners.

The ability to make probabilistic classifications, and the fact that they are eager learners

are two advantages of Bayesian methods.

6-2

Probability

I am assuming you have some basic knowledge of probability. I flip a coin; what is the

probably of it beings a 'heads'? I roll a 6 sided fair die, what is the probability that I roll a '1'?

that sort of thing. I tell you I picked a random 19 year old and have you tell me the probability

of that person being female and without doing any research you say 50%. These are example

of what is called prior probability and is denoted P(h)—the probability of hypothesis h.

Suppose I give you some additional information about that 19 yr. old—the person is a student

at the Frank Lloyd Wright School of Architecture in Arizona. You do a quick Google search,

see that the student body is 86% female and revise your estimate of the likelihood of the

person being female to 86%.

This we denote as P(h|D) —the probability of the hypothesis h given some data D. For

example:

So for a coin:

P(heads) = 0.5

For a six sided dice, the probability of rolling a ‘1’:

P(1) = 1/6

If I have an equal number of 19 yr. old male and

females →

P(female) = .5

P(female | attends Frank Lloyd Wright School) = 0.86

which we could read as “The probability the person is female given

that person attends the Frank Lloyd Wright School is 0.86

PROBABILITY AND NAÏVE BAYES

6-3

The formula is

P(A | B) =

P(A ∩ B)

P(B)

An example.

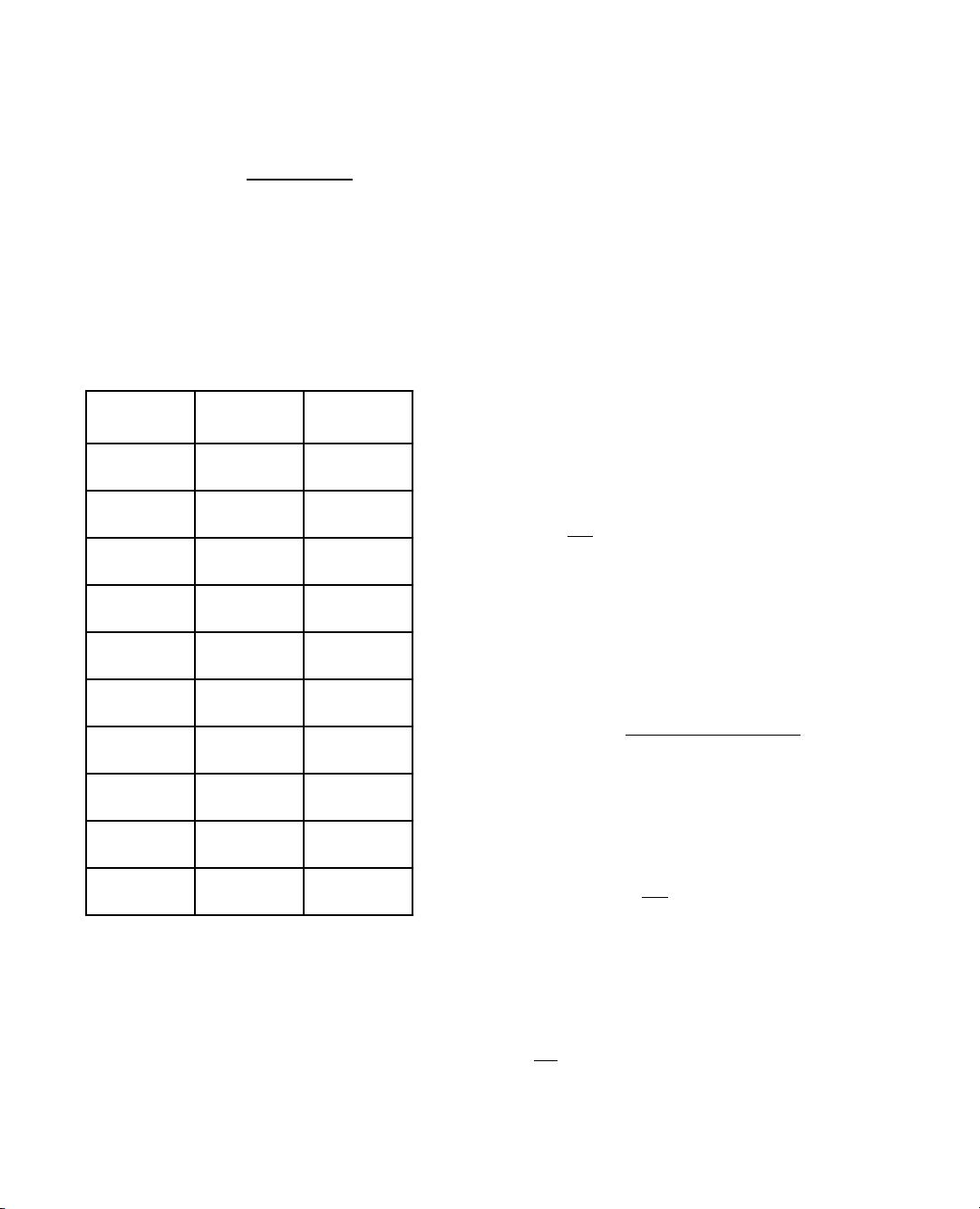
In the following table I list some people and the types of laptops and phones they have:

6-4

name

laptop

phone

Kate

Android

To m

Android

Harry

Android

Annika

Mac

iPhone

Naomi

Mac

Android

Joe

Mac

iPhone

Chakotay

Mac

iPhone

Neelix

Mac

Android

Kes

iPhone

B’Elanna

Mac

iPhone

What is the probability that a randomly

selected person uses an iPhone?

There are 5 iPhone users out of 10 total users so

P(iPhone) =

= 0.5

What is the probability that a randomly selected

person uses an iPhone given that person uses a

Mac laptop?

P(iPhone | mac) =

P(mac ∩ iPhone)

P(mac)

First, there are 4 people who use both a Mac and

an iPhone:

P(mac ∩ iPhone) =

= 0.4

and the probability of a random person using a

mac is

P(mac) =

= 0.6

So the probability of that some person uses an iPhone given that person uses a Mac is

P(iPhone | mac) =

0.4

0.6

= 0.667

That is the formal definition of posterior probability. Sometimes when we implement this we

just use raw counts:

P(iPhone|mac) =

P(iPhone | mac)=

= 0.667

s sharpen your pencil

What’s the probability of a person owning

a mac given that they own an iPhone

i.e., P(mac|iPhone)?

PROBABILITY AND NAÏVE BAYES

6-5

number of people who use a mac and an iPhone

number of people who use a mac

tip

If you feel you need practice with basic probabilities please see the links to

tutorials at guidetodatamining.com.

剩余70页未读，继续阅读

评论收藏

内容反馈

资源评论

资源反馈

评论星级较低，若资源使用遇到问题可联系上传者，3个工作日内问题未解决可申请退款~

weixin_38719540

粉丝: 6
资源: 908

上传资源快速赚钱

我的内容管理展开

我的资源快来上传第一个资源

我的收益

登录查看自己的收益

我的积分登录查看自己的积分

我的C币登录后查看C币余额

我的收藏

我的下载

下载帮助

前往需求广场，查看用户热搜

DataMining-ch6-计算机科学

CS-SBU-DataMining-Msc-3992：Shahid Beheshti大学计算机科学系硕士数据挖掘课程

DataMining-ch4-计算机科学

CS-SBU-DataMining-Msc-projects:沙希德·贝赫什蒂大学计算机科学系硕士数据挖掘课程项目

DataMining-ch5-计算机科学

data mining

Data mining

Data Mining - Mehmed Kantardzic

Data Mining-数据挖掘 Data Mining-数据挖掘 Data Mining-数据挖掘

Learning Data Mining with Python - Second Edition

Web Data Mining - Exploring Hyperlinks, Contents, and Usage Data-2007

Data Mining - Concepts and Techniques

DataMining-ch1-计算机科学

datamining

Datamining

dataMining

Principles of Data Mining-3rd.pdf

DataMining-master.zip

Mathematical Tools for Data Mining-2015.pdf

data mining-2(5).R

Data Mining

最新资源