基于连续时隙探测的防碰撞算法研究基于连续时隙探测的防碰撞算法研究
为进一步提高标签的识别速度,针对动态帧时隙类算法对帧长调整的不灵敏性以及Q算法中Q值调整的高计算复
杂度,提出了一种基于连续时隙探测的RFID防碰撞算法,详细阐述了该算法的思想和运算流程。该算法通过探
测识别帧中连续时隙的应答状况,利用设定的规则调整帧长,使系统工作在最佳状态。仿真结果表明,与标准
QA算法相比,改进的算法缩短了系统4%的识别时延,提高了系统6%的识别速度。
0 引言引言
无线射频识别(Radio Frequency Identification,RFID)是一种利用射频识别方式进行无线非接触双向通信的自动识别技术。
随着物联网技术的日益成熟,RFID技术得到了快速的发展,但其存在的问题也越来越凸显出来。目前RFID技术的主要问题包
括:标准不统一问题、数据安全问题、电磁干扰问题、标签碰撞问题等,其中标签碰撞问题严重制约着RFID的发展,如何有
效解决标签碰撞问题是RFID技术研究的重点和难点。目前解决标签碰撞问题的防碰撞算法主要分为两类
[1]
:基于树类的确定
性算法和基于ALOHA类的随机性防碰撞算法。
基于树类的确定性算法分为二进制树(Binary Search Tree,BT)类和查询树(Query Tree,QT)类算法。在BT类算法中,读
写器逐时隙生成随机数0和1,进而形成新的路径来识别标签。在QT类算法中,读写器根据标签ID的二进制树状结构特点,形
成唯一响应路径的策略来识别标签。学者们根据树类算法的特点,提出大量改进的防碰撞算法
[2-6]
,但仍产生大量的空闲和碰
撞时隙。基于ALOHA的随机性算法
[7-11]
采用时隙随机分配的工作方式,执行过程相对简单,易于实现。当前该类算法又主要
分为动态帧时隙算法(Dynamic Frame Slot Aloha,DFSA)和Q算法。前者通过将帧长设定为估计标签数量的近似值,使系统
以最高的效率识别标签,标签数量估算精度和帧长的动态调整是制约DFSA算法识别效率的主要原因。后者避免了待识别标签
数量的估计,同时解决了DFSA算法在识别帧中不能动态调整帧长的问题,但其使用单一的调整因子不能单独考虑空闲时隙和
碰撞时隙。
本文针对DFSA类算法对帧长调整的不灵敏性以及Q算法中Q值调整的高计算复杂度,提出了基于连续时隙探测的RFID防碰
撞算法(Continuous Slot Detection,CSD)。CSD算法引入了时隙探测的概念,通过判断识别帧中连续时隙的应答情况,动态
调整帧长。仿真结果显示,与其他防碰撞算法相比,CSD算法具有较低的识别时延和较快的识别速度,并且在较多标签存在
的环境下有明显优势。
1 连续时隙探测的防碰撞算法连续时隙探测的防碰撞算法
1.1 CSD算法思想算法思想
针对DFSA类算法对帧长调整的不灵敏性以及Q算法中Q值调整的高计算复杂度,本文提出的CSD算法主要有以下两个方面
的改进:
(1)缓解标签识别初始阶段的标签与帧长不匹配问题。对于DFSA算法,无论当前时隙是空闲还是碰撞,读写器都要查阅完整
个时隙才能调整帧长,因此在标签与帧长不匹配的初始阶段,DFSA无法迅速根据标签数量调整帧长。CSD算法结合理论分析
和实验推导,在大规模标签群下,通过判断初始条件下待识别帧起始3个连续时隙的应答状况,迅速调整帧长,使系统工作在
最优状态。
(2)降低浮点数运算的计算复杂度。计算机中所有的数据均以二进制形式表示,浮点数也不例外。当在大规模标签群时,读
写器多次对浮点参数进行近似计算,不仅造成误差累加,而且降低系统的识别效率。CSD算法利用判断帧中连续3个时隙的状
态替代浮点参数c调整帧长,降低了运算量,加快了识别速度。
1.2 CSD算法关键参数的确定算法关键参数的确定
为了详细描述CSD算法,现定义以下概念:
定义1 标签帧长比α为待识别标签数量n与识别帧长F的比值:
定义2 单位碰撞标签量β
k
为连续碰撞时隙内的每个时隙的标签量,k为连续状态相同的时隙个数。
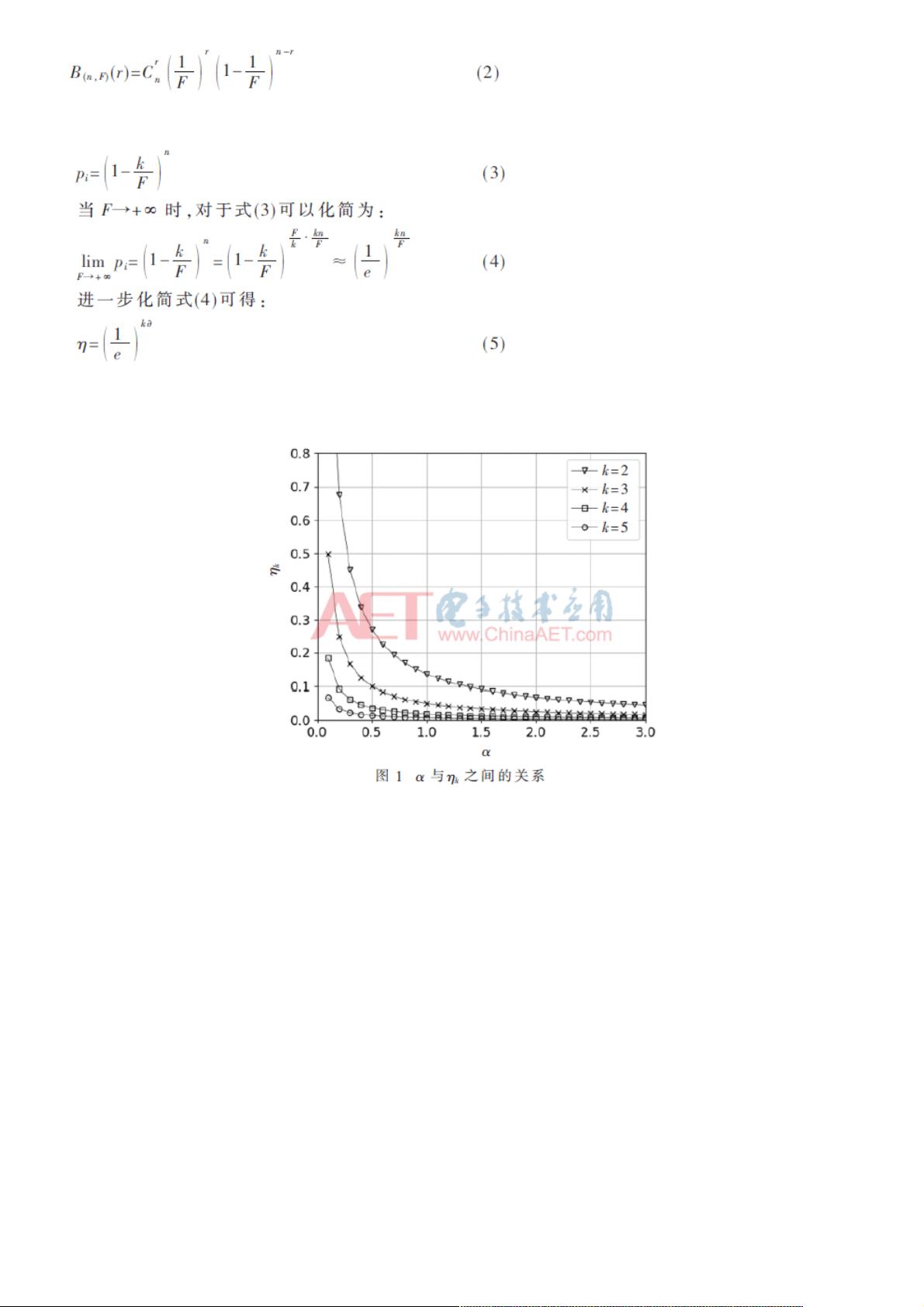
定义3 η
k
表示连续k个空闲时隙发生的概率。
定义4 γ
k
表示连续k个碰撞时隙发生的概率。
定义5 连续碰撞时隙计数器(Continuous Collision Slot Count,CCSC)用于统计连续碰撞时隙的数量;连续空闲时隙计数器
(Continuous Idle Slot Count,CISC)用于统计连续空闲时隙的数量。
1.2.1 连续空闲时隙数量的确定连续空闲时隙数量的确定
标签的碰撞问题从数学的角度上说是一个多重伯努利实验问题。理论条件下一个时隙内出现r个标签可以记为: