没有合适的资源?快使用搜索试试~ 我知道了~
FastRAQ:大数据环境中范围聚合查询的快速方法
资源推荐
资源详情
资源评论

FastRAQ: A Fast Approach to Range-Aggregate
Queries in Big Data Environments
Xiaochun Yun, Member, IEEE, Guangjun Wu, Member, IEEE, Guangyan Zhang,
Keqin Li, and Shupeng Wang
Abstract—Range-aggregate queries are to apply a certain aggregate function on all tuples within given query ranges. Existing
approaches to range-aggregate queries are insufficient to quickly provide accurate results in big data environments. In this paper, we
propose FastRAQ—a fast approach to range-aggregate queries in big data environments. FastRAQ first divides big data into
independent partitions with a balanced partitioning algorithm, and then generates a local estimation sketch for each partition. When a
range-aggregate query request arrives, FastRAQ obtains the result directly by summarizing local estimates from all partitions.
FastRAQ has Oð1Þ time complexity for data updates and Oð
N
PB
Þ time complexity for range-aggregate queries, where N is the number
of distinct tuples for all dimensions, P is the partition number, and B is the bucket number in the histogram. We implement the FastRAQ
approach on the Linux platform, and evaluate its performance with about 10 billions data records. Experimental results demonstrate
that FastRAQ provides range-aggregate query results within a time period two orders of magnitude lower than that of Hive, while the
relative error is less than 3 percent within the given confidence interval.
Index Terms—Balanced partition, big data, multidimensional histogram, range-aggregate query
Ç
1INTRODUCTION
1.1 Motivation
B
IG data analysis can discover trends of various social
aspects and preferences of individual everyday behav-
iours. This provides a new opportunity to explore funda-
mental questions about the complex world [1], [2], [3]. For
example, to build an efficient investment strategy, Preis et al.
[2] analyzed the massive behavioral data sets related to
finance and yielded a profit of even 326 percent higher than
that of a random investment strategy. Choi and Varian [3]
presented estimate sketches to forecast economic indicators,
such as social unemployment, automobile sale, and even
destinations for personal travelling. Currently, it is impor-
tant to provide efficient methods and tools for big data analy-
sis. We give an application example of big data analysis.
Distributed intrusion detection systems (DIDS) monitor and
report anomaly activities or strange patterns on the network
level. A DIDS detects anomalies via statistics information
of summarizing traffic features from diverse sensors to
improve false-alarm rates of detecting coordinated attacks.
Such a scenario motivates a typical range-aggregate query
problem [4] that summarizes aggregated features from
all tuples within given queried ranges. Range-aggregate
queries are important tools in decision management, online
suggestion, trend estimation, and so on. It is a challenging
problem to quickly obtain range-aggregate queries results in
big data environments. The big data involves a significant
increase in data volumes, and the selected tuples maybe
locate in different files or blocks. On the other hand, real-
time systems aim to provide relevant results within seconds
on massive data analysis [5].
The Prefix-sum Cube (PC) method [4], [6] is first used in
OLAP to boost the performance of range-aggregate queries.
All the numerical attribute values are sorted and any range-
aggregate query on a data cube can be answered in constant
time. However, when a new tuple is written into the cube, it
has to recalculate the prefix sums for all dimensions. Hence,
the update time is even exponential in the number of
cube dimensions. Online Aggregation (OLA) is an important
approximate answering approach to speeding range-aggre-
gate queries [7], which has been widely studied in relational
databases [8] and Cloud systems [9], [10], [11], [12]. The OLA
systems provide early estimated returns while the back-
ground computing processes are still running. The returns
are progressively refined and the accuracy is improved in
subsequent stages. But users cannot obtain an appropriate
answering with satisfied accuracy in the early stages.
The sampling and histogram approaches have been uti-
lized in database environments to support approximate
answering or selectivity estimation. However, it can not
acquire acceptable approximations of the underlying data
sets, when data frequency distributions in different dimen-
sions vary significantly.
1.2 Our Contributions
In this paper, we propose FastRAQ—a new approximate
answering approach that acquires accurate estimations
quickly for range-aggregate queries in big data environments.
X. Yun, G. Wu, and S. Wang are with the Institute of Information Engi-
neering, Chinese Academy of Sciences, Beijing 100029, China.
E-mail: {yunxiaochun, wuguangjun, wangshupeng}@iie.ac.cn.
G. Zhang is with the Department of Computer Science and Technology,
Tsinghua University, Beijing 100084, China.
E-mail: gyzh@tsinghua.edu.cn.
K. Li is with the Department of Computer Science, State University of
New York, New Paltz, NY 12561. E-mail: lik@newpaltz.edu
Manuscript received 24 Feb. 2014; revised 26 June 2014; accepted 27 June
2014. Date of publication 29 July 2014; date of current version 10 June 2015.
Recommended for acceptance by R. Ranjan, L. Wang, A. Zomaya,
D. Georgakopoulos, G. Wang, and X.-H. Sun.
For information on obtaining reprints of this article, please send e-mail to:
reprints@ieee.org, and reference the Digital Object Identifier below.
Digital Object Identifier no. 10.1109/TCC.2014.2338325
206 IEEE TRANSACTIONS ON CLOUD COMPUTING, VOL. 3, NO. 2, APRIL/JUNE 2015
2168-7161 ß 2014 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
FastRAQ first divides big data into independent partitions
with a balanced partitioning algorithm, and then generates a
local estimation sketch for each partition. When a range-
aggregate query request arrives, FastRAQ obtains the result
directly by summarizing local estimates from all partitions.
The balanced partitioning algorithm works with a strati-
fied sampling model. It divides all data into different groups
with regard to their attribute values of interest, and further
separates each group into multiple partitions according to
the current data distributions and the number of available
servers. The algorithm can bound the sample errors in each
partition, and can balance the number of records adaptively
among servers when the data distribution and/or the num-
ber of servers changes.
The estimation sketch is a new type of multi-dimensional
histogram that is built according to learned data distribu-
tions. Our multi-dimensional histogram can measure the
quality of tuples distributions more accurately and can sup-
port accurate multi-dimensional cardinality queries. It can
maintain nearly equivalent frequencies for different values
within each histogram bucket, even if the frequency distri-
butions in different dimensions vary significantly.
FastRAQ has Oð1Þ time complexity for data updates and
Oð
N
PB
Þ time complexity for ad-hoc range-aggregate queries,
where N is the number of distinct tuples in all dimensions,
P is the number of partitions, and B is the number of buck-
ets in a histogram. Furthermore, it produces negligible vol-
ume of index data in big data environments.
We implement the FastRAQ approach on the Linux plat-
form, and evaluate its performance with about 10 billions
data records. Experimental results demonstrate that Fas-
tRAQ provides range-aggregate query results within a time
period two orders of magnitude lower than that of Hive,
while the relative error is less than 3 percent within the
given confidence interval.
2OVERVIEW OF THE FASTRAQ APPROACH
2.1 Problem Statement
We consider the range-aggregate problem in big data envi-
ronments, where data sets are stored in distributed servers.
An aggregate function operates on selected ranges, which
are contiguous on multiple domains of the attribute values.
In FastRAQ, the attribute values can be numeric or alpha-
betic. One example of the range-aggregate problem is
shown as follows:
Select exp(AggColumn), other ColName where
l
i1
< ColName
i
<l
i2
opr
l
j1
< ColName
j
<l
j2
opr
...;
In the above query, exp is an aggregate function such as
SUM or COUNT; AggColumn is the dimension of the aggre-
gate operation; l
i1
< ColName
i
<l
i2
and l
j1
< ColName
j
<
l
j2
are the dimensions of ranges queries; opr is a logical oper-
ator including AND and OR logical operations. In the fol-
lowing discussion, AggColumn is called Aggregation-Column,
ColName
i
and ColName
j
are called Index-Columns.
The cost of distributed range-aggregate queries primarily
includes two parts. i.e., the cost of network communication
and the cost of local files scanning. The first cost is produced
by data transmission and synchronization for aggregate
operations when the selected files are stored in different
servers. The second cost is produced by scanning local files
to search the selected tuples. When the size of a data set
increases continuously, the two types of cost will also
increase dramatically. Only when the two types of cost are
minimized, can we obtain faster final range-aggregate
queries results in big data environments.
2.2 Key Idea
To generate a local request result, we design a balanced par-
tition algorithm which works with stratified sampling
model. In each partition, we maintain a sample for values of
the aggregation-column and a multi-dimensional histogram
for values of the index-columns. When a range-aggregate
query request arrives, the local result is the product of the
sample and an estimated cardinality from the histogram.
This reduces the two types of cost simultaneously. It is for-
mulated as
P
M
i¼1
Count
i
Sample
i
, where M is the number
of partitions, Count
i
is the estimated cardinality of the que-
ried ranges, and Sample
i
is the sample for values of aggre-
gation-column in each partition.
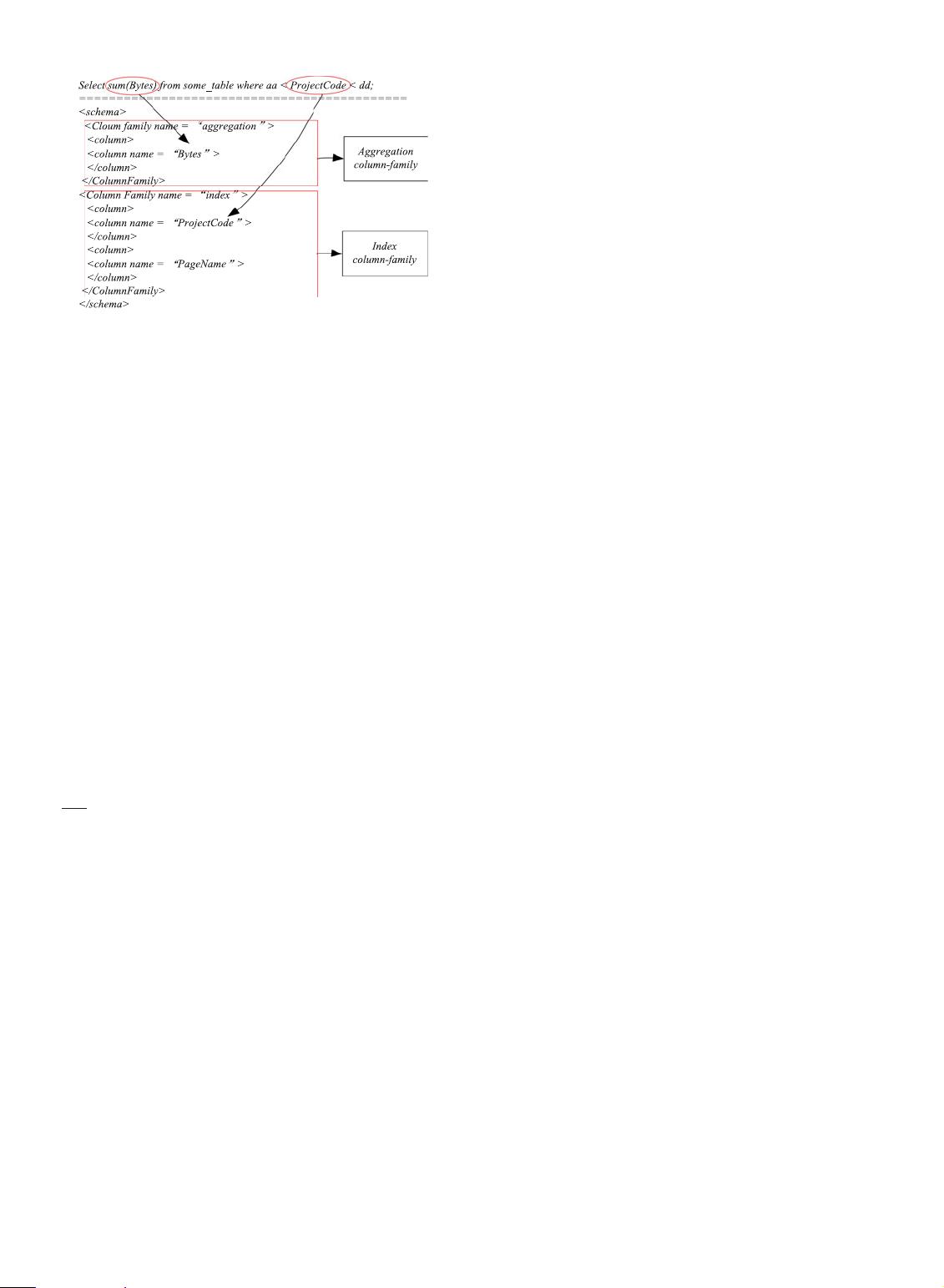
Column-family schema for FastRAQ, which includes
three types of column-families related to range-aggregate
queries. They are aggregation column-family, index column-fam-
ily, and default column-family. The aggregation column-family
includes an aggregation-column, the index column-family
includes multiple index-columns, and the default column-
family includes other columns for further extensions. A
SQL-like DDL and DML can be defined easily from the
schema. An example of column-family schema and SQL-like
range-aggregate query statement is shown in Fig. 1.
In FastRAQ, we divide numerical value space of an
aggregation-column into different groups, and maintain an
estimation sketch in each group to limit relative estimated
errors of range-aggregate paradigm. When a new record is
coming, it is first sent onto a partition in the light of current
data distributions and the number of available servers. In
each partition, the sample and the histogram are updated
respectively by the attribute values of the incoming record.
When a query request arrives, it is delivered into each
partition. We first build cardinality estimator (CE) for the
queried range from the histogram in each partition. Then
we calculate the estimate value in each partition, which is
the product of the sample and the estimated cardinality
from the estimator. The final return for the request is the
sum of all the local estimates. A brief FastRAQ framework
Fig. 1. An example of the column-family schema.
YUN ET AL.: FASTRAQ: A FAST APPROACH TO RANGE-AGGREGATE QUERIES IN BIG DATA ENVIRONMENTS 207
剩余12页未读,继续阅读
资源评论

weixin_38713393
- 粉丝: 8
- 资源: 878
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功