使用幅度分析来测量$$B\rightarrowK\pi\pi\gamma$$B→Kππγ衰减中的光子极化资源-CSDN文库

Open

Access

103 浏览量 2020-03-26 07:08:50 上传评论收藏 973KB PDF 举报

资源推荐

资源详情

资源评论

Eur. Phys. J. C (2019) 79:622

https://doi.org/10.1140/epjc/s10052-019-7127-3

Regular Article - Experimental Physics

Using an amplitude analysis to measure the photon polarisation in

B → K ππγ decays

V. Bellée

1,a

,P.Pais

1,b

, A. Puig Navarro

2,c

,F.Blanc

1,d

, O. Schneider

1,e

, K. Trabelsi

3,f

, G. Veneziano

1,g

Institute of Physics, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

Physik-Institut, Universität Zürich, Zürich, Switzerland

LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France

Received: 26 March 2019 / Accepted: 10 July 2019 / Published online: 25 July 2019

Abstract A method is proposed to measure the photon

polarisation parameter λ

in b → sγ transitions using

an amplitude analysis of B → K ππγ decays. Simpliﬁed

models of the K ππ system are used to simulate B

→

−

γ and B

→ K

−

γ decays, validate the

amplitude analysis method, and demonstrate the feasibility

of a measurement of the λ

parameter irrespective of the

model parameters. Similar sensitivities to λ

are obtained

with both the charged and neutral hadronic systems. In the

absence of any background and distortion due to experimen-

tal effects, the statistical uncertainty expected from an analy-

sis of B

→ K

−

γ decays in an LHCb data set corre-

sponding to an integrated luminosity of 9 fb

−1

is estimated to

be 0.009. A similar measurement using B

→ K

−

decays in a Belle II data sample corresponding to an inte-

grated luminosity of 5 ab

−1

would lead to a statistical uncer-

tainty of 0.018.

1 Introduction

Rare b → sγ ﬂavour-changing neutral-current transitions

are expected to be sensitive to New Physics (NP) effects.

These transitions are allowed only at loop level, and NP

could arise from the exchange of a heavy particle in the

electroweak penguin loop. In the Standard Model (SM), the

recoil s quark that couples to a W boson is left-handed,

causing the photon emitted in b → sγ transitions to be

e-mail: violaine.bellee@epﬂ.ch

e-mail: preema.pais@epﬂ.ch

e-mail: albert.puig@cern.ch

e-mail: fred.blanc@epﬂ.ch

e-mail: olivier.schneider@epﬂ.ch

e-mail: trabelsi@lal.in2p3.fr

e-mail: giovanni.veneziano@alumni.epﬂ.ch

almost completely left-handed. Several theories beyond the

SM predict a signiﬁcant right-handed component for the

photon polarisation: in the minimal supersymmetric model

(MSSM), left-right squark mixing causes a chirality ﬂip

along the gluino line in the electroweak penguin loop [1],

while in some grand uniﬁcation models right-handed neu-

trinos (and the associated right-handed quark coupling)

are expected to enhance the right-handed photon compo-

nent [2].

Various complementary approaches have been proposed

for the determination of the polarisation of the photon in

b → sγ transitions. The ﬁrst one consists in studying the

time-dependent decay rate of B

(s)

→ f

γ decays, where

is a particle or system of particles in a CP eigenstate [3].

An alternative approach involves the study of angular dis-

tributions of the four-body ﬁnal state in B

→ K

∗0



−

decays [4]. Yet another proposed method involves exploit-

ing the angular distributions of the photon and the proton in

the ﬁnal state of Λ

→ Λ

(→ ph)γ decays, where Λ

either the ground state or an excited state of the Λ hyperon

and h is a kaon or a pion [5].

Information on the photon polarisation can also be

obtained from B decays to three hadrons and a photon. This

approach is enabled by the fact that the three ﬁnal-state

hadrons allow the construction of a parity-odd triple prod-

uct that inverts its sign with a change in the photon chirality,

and by the existence of interference between the amplitudes

of the hadronic system [6,7].

In B → K

res

γ decays, where K

res

is a kaonic resonance

decaying to a K ππ ﬁnal state, the required interference

in the K ππ system can arise from several sources. In the

case of a single K

res

state, the helicity amplitudes must con-

tain at least two terms with a non-vanishing relative phase.

This can occur between intermediate resonance amplitudes

in the decay K

res

→ K ππ, between S and D wave ampli-

tudes in the decay, or between two intermediate K

∗

π states

123

622 Page 2 of 15 Eur. Phys. J. C (2019) 79 :622

with different charges, related by isospin symmetry.

Inter-

ference can also appear in the presence of different over-

lapping K

res

states; in fact, the presence of a multitude of

interfering resonances makes it very difﬁcult to distinguish

them, thus complicating the interpretation of the observed

distributions.

A simpliﬁed approach to the study of the photon polarisa-

tion consists in exploiting the distribution of the polar angle

of the photon with respect to the hadronic decay plane inte-

grating over the resonance content of the K ππ system [6].

Using 3 fb

−1

of pp collisions at the LHC, the LHCb collab-

oration determined the shape of this distribution and the up-

down asymmetry between the number of events with photons

emitted on either side of the plane [8]. The up-down asymme-

try was found to differ from zero by 5.2 standard deviations.

As this asymmetry is expected to be proportional to the pho-

ton polarisation parameter λ

, this result represents the ﬁrst

observation of a parity-violating nonzero photon polarisa-

tion in b → sγ transitions. The proportionality coefﬁcient

between the up-down asymmetry and λ

depends on the res-

onance content of the K ππ system, and in particular on the

interference pattern between the various decay modes. With-

out precise knowledge of these amplitudes, a measurement

of the up-down asymmetry cannot be translated into a photon

polarisation value.

In this paper, a method to determine the value of the

photon polarisation parameter by means of an amplitude

analysis of the K ππγ system is proposed. It is organ-

ised as follows: a description of the up-down asymme-

try and its limitations in extracting a value for the photon

polarisation parameter are detailed in Sect. 2. In Sect. 3,

a general expression for the B → K ππγ decay rate

in terms of a photon polarisation parameter is derived,

the amplitude formalism is described, and the ﬁt method

used for the amplitude analysis is explained. In Sect. 4,

results for simulated data sets with assumed models of

→ K

−

γ and B

→ K

−

γ decays are pre-

sented. Statistical sensitivities on the photon polarisation

parameter are quoted for these models, assuming no back-

ground and no experimental effect. Conclusions are drawn

in Sect. 5.

2 Motivation

→ K

−

γ and B

→ K

−

γ decays can be

described in terms of ﬁve independent variables: two angles

(cos θ and χ) that describe the direction of the photon in the

rest frame of the kaonic resonance K

res

, and three squared

invariant masses (s

123

, s

), where the indices 1, 2 and 3

This last type of interference is possible only in decays containing a

in the ﬁnal state.

Fig. 1 Deﬁnitions of the angular variables used to describe the K ππγ

system. The indices 1, 2 and 3 refer respectively to the ﬁnal-state π

−

and K

in B

→ K

−

γ decays, and to π

−

, π

and K

→ K

−

γ decays

refer respectively to the ﬁnal-state π

, π

−

and K

for the

charged decay mode, and to π

−

, π

and K

for the neutral

decay mode.

As illustrated in Fig. 1 for B

→ K

−

γ decays, in

the rest frame of the kaonic resonance K

res

, the normal to the

hadronic decay plane is denoted by

n = (p

×p

)/|p

×p

The polar angle θ is the angle between

n and the opposite of

the photon momentum, so that cos θ =−

n · p

/|p

The

angle χ is deﬁned from

cos χ =

(

n × p

) · (

n × p

)

n × p

, (1)

sin χ =

(

n × p

) × (

n × p

)

n × p

n. (2)

The B → K ππγ differential branching fraction has the

following dependence on cos θ [7]:

dΓ(B → K

res

γ → K ππγ)

123

dχ dcos θ



i=0,2,4

123

, s

,χ)cos

+ λ



j=1,3

123

, s

,χ)cos

θ. (3)

Integrating Eq. 3 over the squared invariant masses and χ ,

the up-down asymmetry (A

) is deﬁned as [6,7]

≡



dcos θ

dΓ

dcos θ

−



−1

dcos θ

dΓ

dcos θ



−1

dcos θ

dΓ

dcos θ

, (4)

where the terms in even powers of cos θ disappear, and the

resulting asymmetry is directly proportional to λ

with a pro-

This deﬁnition of the polar angle corresponds to the one used in

Ref. [7] and does not match the one in Ref. [8].

123

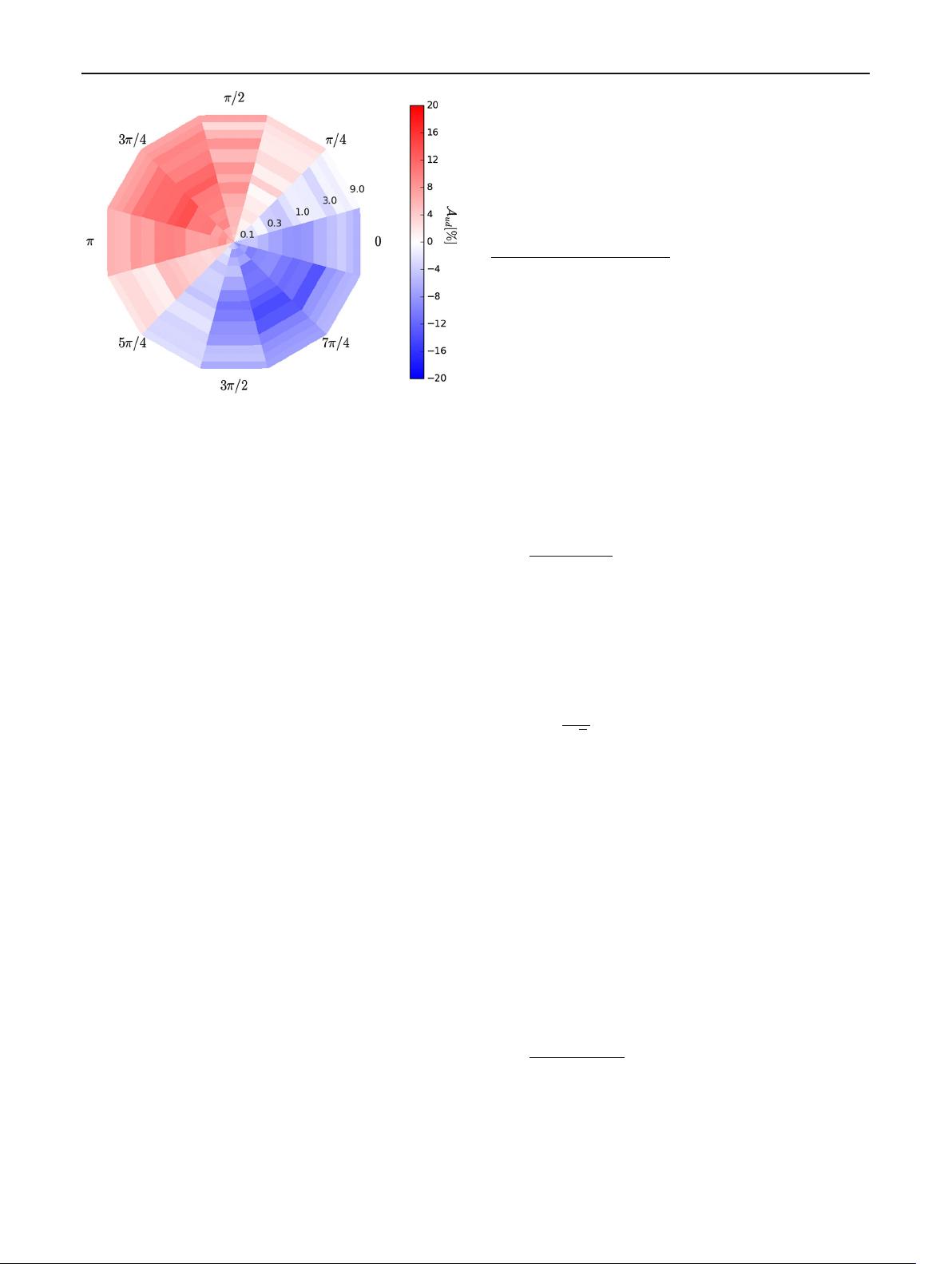
Eur. Phys. J. C (2019) 79 :622 Page 3 of 15 622

Fig. 2 Up-down asymmetry A

for simulated samples of B

→

(1270)

γ decays governed by two amplitudes only, K

(1270)

→

ρ(770)

and K

(1270)

→ K

∗

(892)

, shown as a function of

the generated ratio of fractions (radial coordinate, from 0.1 to 9.0) and

phase difference between the two amplitudes (polar coordinate)

portionality coefﬁcient that depends on the resonance content

of the K ππ system.

The effects of the resonant structure of the K ππ system

on A

can be illustrated using a simpliﬁed B

→ K

res

model containing only two amplitudes corresponding to

the decays K

(1270)

→ K

ρ(770)

and K

(1270)

→

∗

(892)

with ρ(770)

→ π

−

and K

∗

(892)

→

−

. Simulated samples of decays containing only right-

handed photons are generated with different relative frac-

tions (as deﬁned in Eq. 18) and phase differences between

these amplitudes, and the up-down asymmetry is computed

for each of them. The results in Fig. 2 show that the up-

down asymmetry varies widely depending on the phase

difference between the amplitudes, while it is less depen-

dent on the relative fraction. This implies that, even in this

simple model, the proportionality coefﬁcient that relates

the up-down asymmetry to the photon polarisation param-

eter depends strongly on the phase difference between the

amplitudes, making the knowledge of this phase essen-

tial to measure the value of λ

; additionally, for some

values of the relative phase, the proportionality coefﬁ-

cient is null, indicating that the measurement of the up-

down asymmetry is not sensitive to λ

in such conﬁgura-

tions.

To overcome these difﬁculties and measure the photon

polarisation, we propose an analysis that combines informa-

tion from the angular variables and the squared invariant-

mass distributions in order to characterise the interferences

between decay processes and their effect on λ

3 Method

3.1 Photon polarisation parameter

The differential decay rate for B → K ππγ decays that pro-

ceed through a single resonance K

res

can be written as [7]

dΓ(B → K

res

(→ K ππ)γ)

123

=|c

123

+|c

123

, (5)

where s

123

is the invariant mass of the K ππ system, c

and

are the right- and left-handed weak radiative decay ampli-

tudes, T

123

) is the propagator associated to resonance

res

, and A

and A

are the strong decay amplitudes for

res, R/L

→ K ππ. The right- and left-handed amplitudes do

not interfere since the photon polarisation is an observable

quantity. For a given resonance K

res

, a photon polarisation

parameter λ

is deﬁned in terms of the weak radiative decay

amplitudes,

≡

−|c

+|c

. (6)

Using an argument of parity invariance in strong interac-

tions, detailed in Ref. [2], the weak radiative decay ampli-

tudes associated with a resonance K

res

in decays of a B

meson can be written as [7,9]





=−

√

∗



eff

(0) + h



(−1)

−1

(0) + h



, (7)

where G

is the Fermi constant, V

and V

∗

are CKM matrix

elements, P

and J

are the parity and spin of the K

res

res-

onance, g

(0) is the process-dependent hadronic form fac-

tor, C

eff

and C



are the radiative Wilson coefﬁcients, and

the quantities h

R/L

encode remaining contributions from the

1−6

and Q

hadronic operators (see Ref. [9]formore

details). The coefﬁcient C

eff

includes “effective” linear con-

tributions from the other coefﬁcients C

1−6

in order to make

it regularisation- and renormalisation-scheme independent,

as discussed in Ref. [10]. Assuming that the h

R/L

terms are

small enough to be neglected in the expressions of c

and

, the photon polarisation parameter reduces to

eff

−|C



eff

+|C



≡ λ

, (8)

i.e., the photon polarisation in the weak decay B

→ K

res

is the same for all kaonic resonances K

res

and it can be

123

剩余14页未读，继续阅读

评论收藏

内容反馈

weixin_38711333

粉丝: 4
资源: 976

使用幅度分析来测量$$ B \ rightarrow K \ pi \ pi \ gamma $$ B→Kππγ衰减中的光子极化

最新资源

使用幅度分析来测量$$ B \ rightarrow K \ pi \ pi \ gamma $$ B→Kππγ衰减中的光子极化

衰减暗物质发射的光子的极化

在OKA实验中研究衰落$$ K ^ {+} \ rightarrow \ pi ^ {+} \ pi ^ {-} \ pi ^ {+} \ gamma $$ K +→π+π-π+γ

异常的希格斯三线性自耦合对$$ h \ rightarrow \ gamma \，Z $$ h→γZ衰减的影响

$$ B \ rightarrow D ^ {** \ bar {\ nu} l $$ B→D ∗ν¯l衰减的螺旋度

衰减$$ h \ rightarrow Z \ gamma $$ h→Zγ的一般一环公式

$$ \ Lambda _b $$Λb衰减为$$ \ Lambda _c ^ * \ ell \ bar {\ nu __ell $$Λc∗ℓν¯ℓ和$$ \ Lambda _c ^ * \ pi ^-$$Λc ∗π-$$ [\ Lambda _c ^ * = \ Lambda _c（2595）$$ [Λc∗ =Λc（2595）和$$ \ Lambda _c（2625）] $$Λc（2625）]和​​重夸克自旋对称

在光锥和规则内的$$ D \ rightarrow \ rho $$ D→ρ半轻子和辐射衰变

辐射b重子衰变以测量光子和b重子极化

在LHC上以$$ \ gamma \ gamma $$γγ相互作用探测X（4350）

三体辐射衰减$$ B_s \ rightarrow \ phi \ bar {K} ^ 0 \ gamma $$ &lt;math&gt; <mrow> <msub> <mi> B </ mi> <mi> s </ mi> </ msub> <mo>→</ mo> <mi> ϕ </ mi> <msup> <mrow> <mover> <mrow> <mi> K </ mi> </ mrow> <mrow> <mo>？&lt; / mo> </ mrow> </ mover> </ mrow> <mn

D波对类似光子的$$ V \ rightarrow Q {\ bar {Q}} $$ &lt;math&gt; <mrow> <mi> V </ mi> <mo>→</ mo> <mi> Q </ mi> <mover> <mrow> <mi> Q </ mi> </ mrow> <mrow> <mo>¯</ mo> </ mrow> </ mover> </ mrow> &lt;/ math&gt;过渡

纯轻子的$$ B ^ * _ s $$ Bs ∗衰变中的新物理效应

由$$ | V_ {cb} | $$ | Vcb |的树级确定产生的$$ \ Delta M_ {d} $$ΔMd-异常。 和角度$$ \ gamma $$γ

$$ D ^ 0（\ bar {D} ^ 0）\ rightarrow f $$ D0（D¯0）→f有效宽度不对称中的新物理签名

希格斯光子共振

重新评估B \ $$ \ overline {B} $$→X sγ衰减的不确定性

大型强子对撞机中$$ t {\ bar {t}} $$ tt和$$ t {\ bar {t}} \γ$$ttγ产生的单个轻子电荷不对称

马约拉纳中微子在B衰变中具有有效的相互作用

B-LSSM中夸克的顶级夸克衰变并违反风味

在s = 13 $$ \ sqrt {s} = 13 $$的pp碰撞中，测量Zγ→ννγ$$ Z \ gamma \ to \ nu \ overline {\ nu} \ gamma $$生产截面 带有ATLAS检测器的TeV和对异常三重玻色子-玻色子耦合的限制

新尺度玻色子$$ W ^ \素数$$ W'和带电B和D介子的辐射轻子衰变

探索异常$$ tq \ gamma $$ &lt;math&gt; <mrow> <mi> t </ mi> <mi> q </ mi> <mi>γ</ mi> </ mrow> &lt;/ math&gt;和tqg耦合 通过与FCC-hh的光子关联的单顶生产

LHC上t tγ/ t t $$ $$ t \ overline {t} \ gamma / t \ overline {t} $$横截面比率的精确预测

搜索π0衰变中不可见的暗光子的产生

搜索$$ \ mathrm {Z} $$ Z和希格斯玻色子到$$ {\ mathrm {J} / \ psi} $$ J /ψ和光子质子-质子碰撞中$$ \ sqrt { s} $$ s = 13 $$ \，\ text {TeV} $$ TeV

电子-正电子碰撞中的X（16.7）产生

最新资源

$$ \ Lambda _b $$Λb衰减为$$ \ Lambda _c ^ * \ ell \ bar {\ nu __ell $$Λc∗ℓν¯ℓ和$$ \ Lambda _c ^ * \ pi ^-$$Λc ∗π-$$ [\ Lambda _c ^ * = \ Lambda _c（2595）$$ [Λc∗ =Λc（2595）和$$ \ Lambda _c（2625）] $$Λc（2625）]和重夸克自旋对称

三体辐射衰减$$ B_s \ rightarrow \ phi \ bar {K} ^ 0 \ gamma $$ <math> <mrow> <msub> <mi> B </ mi> <mi> s </ mi> </ msub> <mo>→</ mo> <mi> ϕ </ mi> <msup> <mrow> <mover> <mrow> <mi> K </ mi> </ mrow> <mrow> <mo>？< / mo> </ mrow> </ mover> </ mrow> <mn

D波对类似光子的$$ V \ rightarrow Q {\ bar {Q}} $$ <math> <mrow> <mi> V </ mi> <mo>→</ mo> <mi> Q </ mi> <mover> <mrow> <mi> Q </ mi> </ mrow> <mrow> <mo>¯</ mo> </ mrow> </ mover> </ mrow> </ math>过渡

由$$ | V_ {cb} | $$ | Vcb |的树级确定产生的$$ \ Delta M_ {d} $$ΔMd-异常。和角度$$ \ gamma $$γ

在s = 13 $$ \ sqrt {s} = 13 $$的pp碰撞中，测量Zγ→ννγ$$ Z \ gamma \ to \ nu \ overline {\ nu} \ gamma $$生产截面带有ATLAS检测器的TeV和对异常三重玻色子-玻色子耦合的限制

探索异常$$ tq \ gamma $$ <math> <mrow> <mi> t </ mi> <mi> q </ mi> <mi>γ</ mi> </ mrow> </ math>和tqg耦合通过与FCC-hh的光子关联的单顶生产