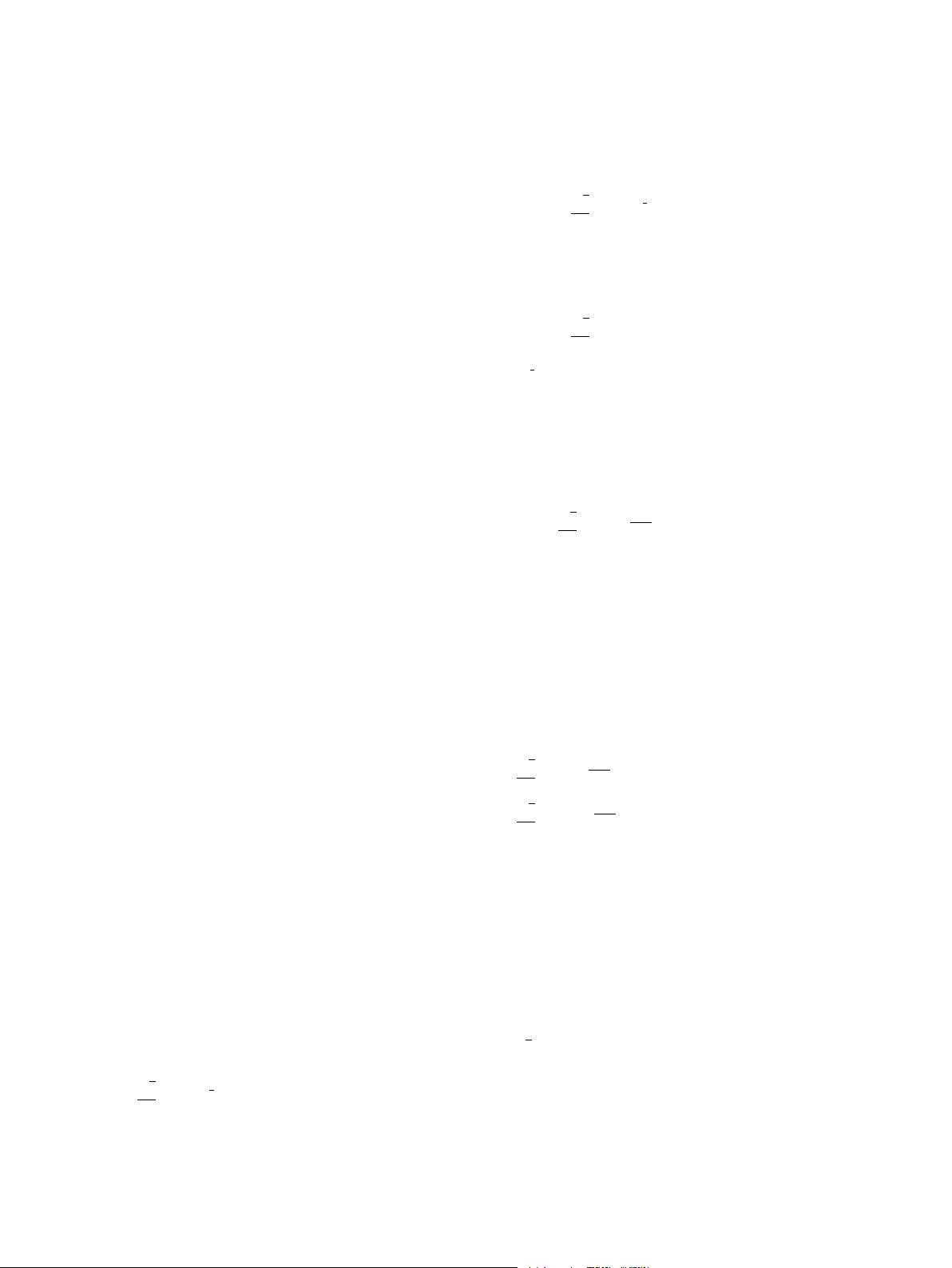
Optics Communications 410 (2018) 389–395
Contents lists available at ScienceDirect
Optics Communications
journal homepage: www.elsevier.com/locate/optcom
Simultaneously frequency down-conversion, independent multichannel
phase shifting and zero-IF receiving using a phase modulator in a sagnac
loop and balanced detection
Zihang Zhu *, Shanghong Zhao, Xuan Li, Tao Lin, Dapeng Hu
School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China
a r t i c l e i n f o
Keywords:
Frequency down-conversion
Multichannel phase shift
Zero-IF receiving
Phase modulator
Balanced detection
a b s t r a c t
Photonic microwave frequency down-conversion with independent multichannel phase shifting and zero-
intermediate frequency (IF) receiving is proposed and demonstrated by simulation. By combined use of a phase
modulator (PM) in a sagnac loop and an optical bandpass filter (OBPF), orthogonal polarized carrier suppression
single sideband (CS-SSB) signals are obtained. By adjusting the polarization controllers (PCs) to introduce the
phase difference in the optical domain and using balanced detection to eliminate the direct current components,
the phase of the generated IF signal can be arbitrarily tuned. Besides, the radio frequency (RF) vector signal can
be also frequency down-converted to baseband directly by choosing two quadrature channels. In the simulation,
high gain and continuously tunable phase shifts over the 360 degree range are verified. Furthermore, 2.5 Gbit/s
RF vector signals centered at 10 GHz with different modulation formats are successfully demodulated.
© 2017 Elsevier B.V. All rights reserved.
1. Introduction
Microwave frequency conversion and phase shifting are two es-
sential functions in the transmitter and receiver of many electronic
systems, such as phase arrayed radar, wideband wireless communica-
tion, satellite payload, electronic warfare, and deep space exploration.
For example, in millimeter-wave phase arrayed radar systems, on the
one hand, a continuous full 360
◦
tunable wideband phase shifter is
a key component for phase-array beam pointing [1]. On the other
hand, radio frequency (RF) signals should be down-converted into
intermediate frequency (IF) signals at the receiver [2]. Thus, it is
desirable to implement frequency down-conversion and phase shifting
simultaneously. Besides, an important part of a modern radar system is
the in-phase and quadrature (I/Q) detector, which enables the extraction
of both real and imaginary parts of the reflected radar signal [3]. The
image product is naturally canceled out in I/Q down conversion without
filtering, so the receiver becomes frequency agile and versatile with
different or multiple operating bands. Meanwhile, as compared with
the IF signal in the super heterodyne receiver, the I/Q baseband signals
have lower requirements for the operating frequency and sampling rate
of the analog-to-digital converter (ADC).
One important characteristic of modern radar system is frequency
agility [3], which means the receiver must be able to operate at any
*
Corresponding author.
E-mail address: zihangzhu@fudan.edu.cn (Z. Zhu).
frequency in which the radar signal is being transmitted. The higher
the frequency hopping range, the more difficult it is to intercept or jam
the signal. Thus, it is necessary to realize wideband frequency down-
conversion, multichannel phase shifting, and zero-IF receiving. The im-
plementation of such a receiver using traditional microwave techniques
could be difficult, particularly when operating over a broad frequency
range, which is mainly due to the frequency-dependent characteristics
of RF components. On the other hand, microwave photonic systems
are able to become reconfigured electronically to operate at different
frequencies over a broad frequency range and, thus, could be considered
for such an application [4–7].
Recently, various photonic microwave frequency down-conversion
methods have been proposed, including two cascaded MZMs biased at
the quadrature points [8], dual-parallel MZM (DP-MZM) [9], optoelec-
tronic oscillator based on a single dual-drive MZM (DD-MZM) [10].
Furthermore, many photonic microwave phase shifting schemes have
also been studied, such as the combined use of a phase modulator and an
optical filter [11], two cascaded polarization modulators (PolMs) [12],
nonlinear polarization rotation in a highly nonlinear fiber [13], and
so on. However, the above approaches cannot realize frequency down-
conversion and phase shifting simultaneously. In fact, combining both
functions into a simple compact configuration can not only simplify
https://doi.org/10.1016/j.optcom.2017.10.044
Received 26 August 2017; Received in revised form 16 October 2017; Accepted 21 October 2017
0030-4018/© 2017 Elsevier B.V. All rights reserved.
剩余6页未读，继续阅读
资源评论
