收稿日期 :2002‐10‐28 ;修改稿收到日期 :2003‐10‐31畅
基金项目 :国家自然科学基金(50075075)资助项目 畅
作者简介 :刘德义(1969‐) ,男 ,博士生 ;
申光宪
倡
(1935‐) ,男 ,教授 ,博士生导师 畅
第21卷第4期
2004 年 8 月
计 算 力 学 学 报
Chinese Journal of Computational Mechanics
Vol .21 ,No .4
August 2004
文章编号 :1007‐4708(2004)04‐0464‐06
三 维 弹 性 快 速 多 极 边 界 元 法
刘德义 , 申光宪
倡
(燕山大学 轧机研究所 ,秦皇岛 066004)
摘 要 :将静电场多极展开法和广义极小残值法结合于三维弹性问题的边界元法 ,使其求解的计算量及所需内存量同节点的
自由度总数成正比 ,变革计算结构 ,加快求解速度以适应大规模数值计算 。 两者结合的关键点在于边界元法基本解的合理分
解 ,并用广义极小残值法(GMRES)求解方程 。 轧机支承辊变形场大规模数值算例的总自由度数首次达 N = 34008 并获得成
功 。 清晰地描述了支承辊和工作辊接触区的辊型 。
关键词 :边界元法 ;多极展开法 ;广义极小残值法 ;误差分析
中图分类号 :O241 .6 文献标识码 :A
1 引 言
传统的边界元法在微机求解三维弹性问题的规模
小 ,其制约因素主要有必须建立方程组的系数矩阵且是
满秩的 ,没有稀疏性和对称性 。 因此 ,需要大容量的内
存 ,而方程组的求解一般采用高斯消去法或由它演变得
到的其他方法 。 这种计算结构 ,要求解 N 个未知数问题
所需要的内存量为 O(N
2
)和 O(N
3
)次运算 ,当 N > 2000
时难以在微机上完成计算 。
多极展开法是求解静电场问题的方法 ,它体现了正
如力学圣维南原理一样将电荷(或力源)的远近不同影响
区分开来加以分别处理的科学思想 ,应用于传统的边界
元法中 ,更新其计算结构 ,给出求解三维弹性问题的 O
(N)方法 。
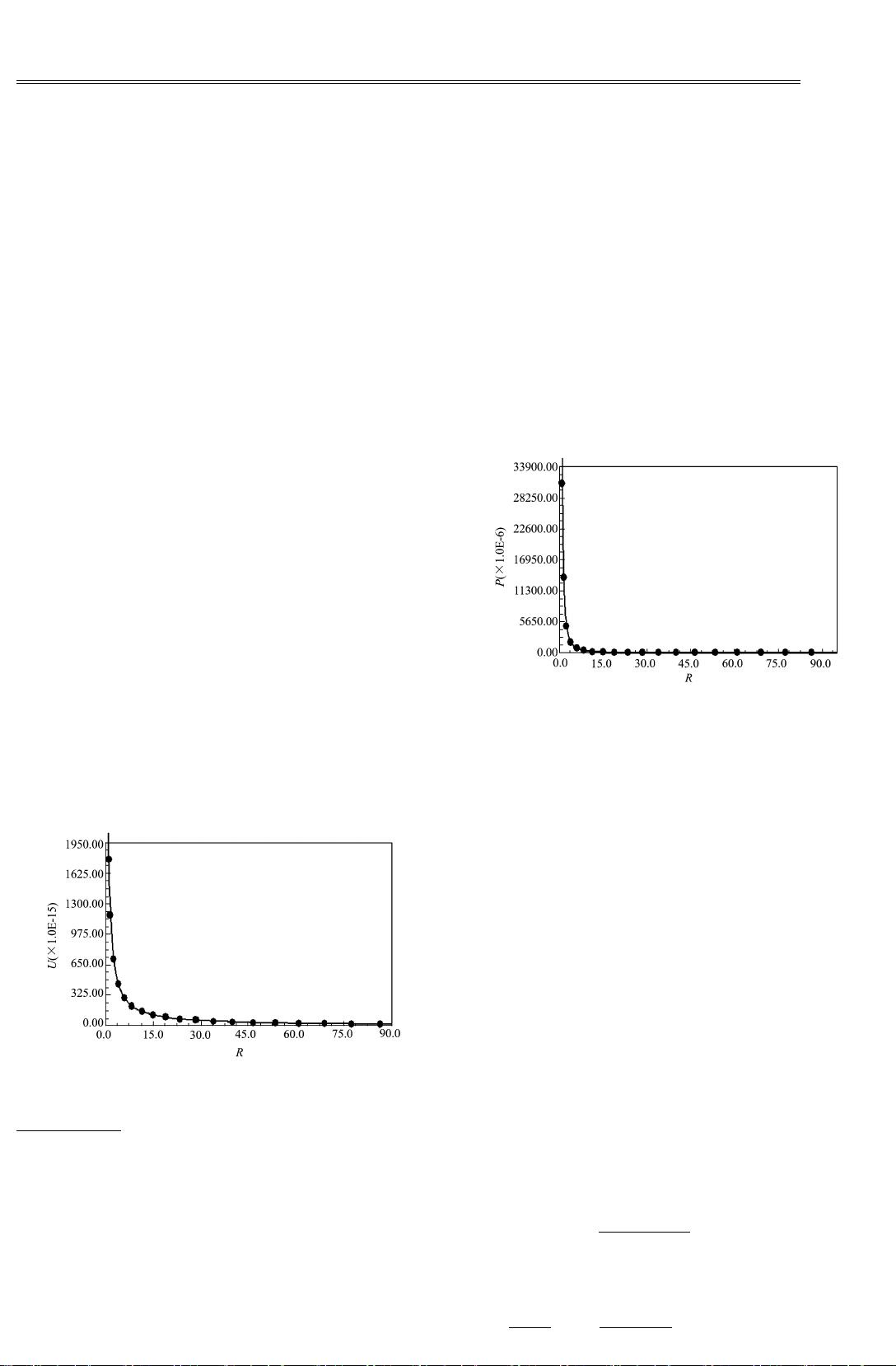
图 1 位移基本解 U 随 R (
ψ
=
θ
=
45
°
) 的变化趋势
Fig .1 T he change of fundamental solution(U ) relay on R
图 2 面力基本解 P 随 R (
ψ
=
θ
=
45
°
) 的变化趋势
Fig .2 T he change of fundamental solution( P) relay on R
本法的计算结构有两点 。第一 ,基于基本解函数特
征(见图 1 和图 2) ,将源点对边界的积分分成两个部分 ,
近处用传统方法 ,远处用多极展开法 。第二 ,用广义极小
残值法(GM RES) 求解方程但不形成系数总矩阵 ,每一
步迭代中的矩阵乘法用多极展开法 。
轧机支承辊的辊型对带材板形质量 (即平直度) 有
重要影响 ,但受问题复杂性和微机解题规模的限制 ,一直
未能给出清晰的辊型 。三维弹性问题快速多极边界元法
可以在微机上精确模拟大型带钢轧机支承辊的辊型 。
2 多极展开法
[1 ]
设有 N 个强度为
q
1
,
q
2
,… ,
q
N
的电荷位于点 X
1
(x
1
,
y
1
,z
1
) ,X
2
(x
2
,
y
2
,z
2
) ,… ,X
N
(x
N
,
y
N
,z
N
) ,并且点 X
1
,
X
2
,… ,X
N
位于圆心在原点 X
0
,半径为 a 的球内 。则有 ,
任意点 X
=
(x ,
y
,z) ∈ R
3
,在 X
-
X
0
>
a时 ,由这 N 个
电荷在 X 点产生的电势
Φ
(X) 为
Φ
(X ) =
∑
∞
j
=
0
1
(X
-
X
0
)
j
+
1
∑
N
i
=
1
q
i
(X
i
-
X
0
)
j
(1)
对任意的展开相数 k(k
≥
1) ,有
‖
∑
N
i
=
1
q
i
X
-
X
i
-
∑
K
j
=
0
1
(X
-
X
0
)
j
+
1
∑
N
i
=
1
q
i
(X
i
-
X
0
)
j
‖
≤















