一种高速模(2n-2p-1)乘法器的设计

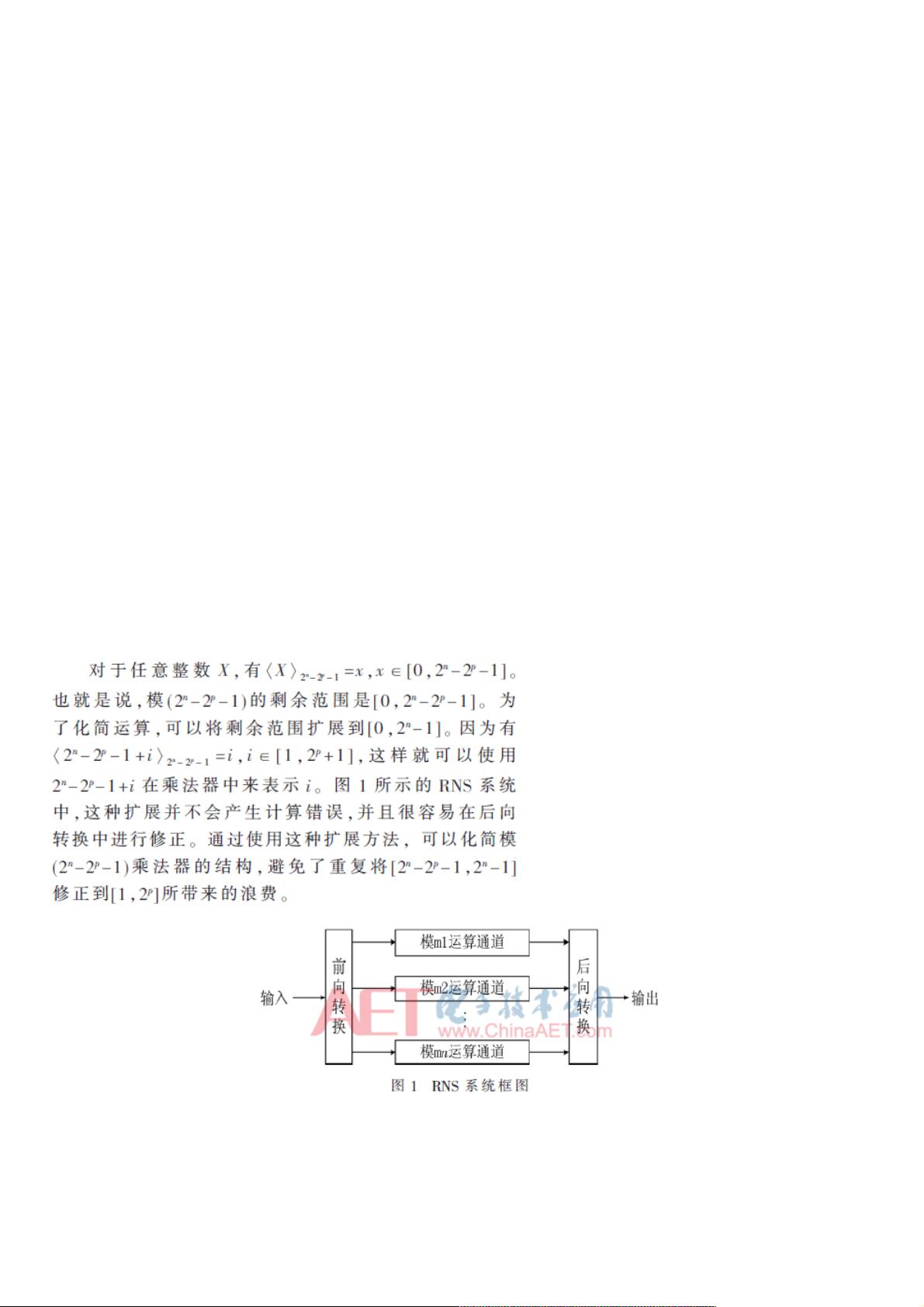
结合余数系统以及模乘法器本身的特点，一种高速的模(2n-2p-1)乘法器被提出。得益于剩余范围的扩展和新型的部分积压缩树的采用，该设计相较于传统的模乘法器在关键路径上减少了一个长度为2n的加法器且避免了此类Booth编码模乘法器中复杂的负数修正问题。在90 nm工艺下的综合结果表明，该模乘(2n-2p-1)乘法器相较当前的模(2n-2p-1)乘法器有10.4%到49%的延迟性能提升。 本文探讨的是一种针对余数系统优化的高速模(2n-2p-1)乘法器设计，旨在解决传统模乘法器中的速度瓶颈和负数修正问题。模(2n-2p-1)乘法器在数字信号处理、加密算法和密码学等领域有广泛应用，因此提高其运算速度至关重要。 文章介绍了TDM（Three-Dimensional Minimization）压缩树算法。TDM算法是一种用于优化部分积压缩结构的方法，通过调整全加器的连接方式，使得最长和最短延迟路径相互匹配，从而提高整体运算速度。同时，TDM算法还支持将全加器替换为4:2等压缩器，以进一步提升性能。虽然TDM压缩树相比Booth编码的混合型压缩结构可能会增加面积，但因其避免了处理负数修正，总延迟实际上更小，尤其适合无符号且位数不高的乘法操作。 文中提到了剩余范围的扩展方法。这是一种无开销的技术，能够将余数范围从[0, 2n-2p-1]扩展到[0, 2n-1]。这一扩展为简化模(2n-2p-1)乘法器的结构提供了便利，减少了计算过程中对负数修正的需求。 接下来，文章详细描述了高速模(2n-2p-1)乘法器的具体结构。乘法器使用TDM压缩树来压缩部分积，并通过一系列级联的Carry-Save Adders (CSAs)和二进制加法器进行计算。乘法过程分为多个步骤，包括部分积的压缩、折叠、以及最终结果的生成。这个设计的关键在于减少了关键路径上的一个2n位加法器，并避免了Booth编码中的负数修正问题，从而提高了运算速度。 在90纳米工艺下进行的综合结果显示，这种新的模(2n-2p-1)乘法器相比于现有设计有10.4%到49%的延迟性能提升。这表明了该设计的有效性和优势。 文章进行了分析与比较，将提出的模乘法器与文献中其他模乘法器进行对比，进一步证明了新设计在延迟性能上的优越性。 本文提出的高速模(2n-2p-1)乘法器利用TDM压缩树和剩余范围扩展技术，成功地优化了乘法器结构，降低了关键路径延迟，提升了运算效率。这一成果对于提高数字电路特别是涉及模运算的系统的性能具有重要意义。