
http://www.paper.edu.cn
Belnap’s four-valued logic is useful for reasoning with inconsistent and incomplete infor-
mation. Classical logic has two truth values t, f of excluded middle. The two values negate each
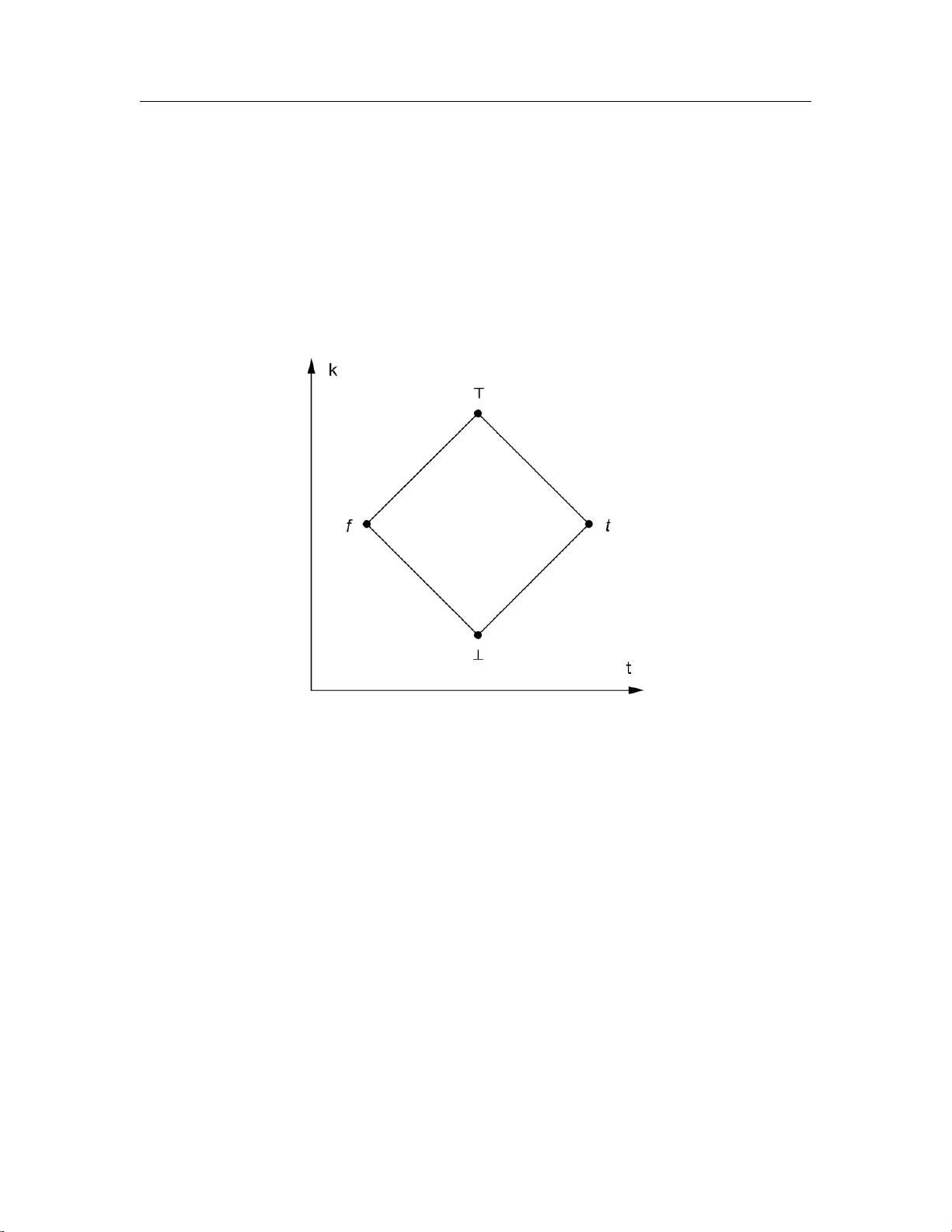
other, i.e., ∼ t = f, ∼ f = t. The four-valued logic as non-classical logic, two additional truth
values ⊤, ⊥ are introduced to represent “both truth and false” (over information, i.e., incon-
sistency in classical logic) and “neither true nor false” (no information, i.e., incompleteness in
classical logic) respectively. But the negation ∼ does not affect ⊤ and ⊥, i.e., ∼ ⊤ = ⊤, ∼ ⊥ = ⊥.
Unlike in classical logic, Belnap’s logic has no tautologies, and the excluded middle is not valid
in it. This implies that the definition of the material implication as in classical logic is not
adequate there for representing entailment. Thus there are different kinds of the implication
need to be consider for the implication inference [1, 2]. In [5, 4], it is observed that the con-
nective of so-called conflation ≀ is natural dual of the negation in the bilatice semantics, i.e.,
≀⊤ = ⊥, ≀⊥ = ⊤. However, it is unclear that logical role of the conflation was introduced into
the four-valued logic.
Belnap’s four-valued logic is paraconsistent in a sense that it is nontrivial, i.e., no everything
follows from a single contradiction. Like in classical logic, a proposition is satisfied if it takes
the true value, which is t or ⊤. A proposition has the value ⊤ means it is true in a sense that
there is information for the judgment of the truth even if it could be conflict. If a proposition
is contradictory in classical logic, it can be taken the value ⊤ now, and then that there is a
proposition which is not satisfied can not be followed from it. Thus it excludes real contradiction
from classical logic. In philosophy, there are two basic kinds of contradictions. The real
contradicting information like in classical logic means it is not reconcilling and the conflicting
information means there is information for and against it. By the negation and conflation
together, we can discriminate different contradictions as we shall see in later.
The four values structure is the minimal bilattice, exactly as the structure that is based
on classical two values is the minimal Boolean algebra. The four-valued logic is very similar to
extension of two-valued logic. We emphasis on the model-theoretic semantics of the four values
structure rather than the bilattice-based algebraic one and consider it as a normal extension of
classical logic in the following considerations. First, we consider here on standard extensional
connectives of the language with negation and conflation. Actually, the implication in Belnap’s
four-valued logic does not satisfy so-called normal condition of an implication [6], i.e., A → B
takes a non-designated truth iff A takes a designated one and B takes a non-designated one.
The implication → has the strongest possible regular extensions of classical two-valued truth
tables, i.e., they have a truth value in each position where any regular extension of two-valued
truth tables can have the same one. Second, we consider a notion of strong consistency to
capture the real contradiction like in classical logic. The classical logic can be exactly regarded
as a sublogic of the four-valued logic. It is not straightforward to have an axiomization of
Belnap’s logic, though there are some other proof systems [2]. We shall have an axiomization
- 2 -




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功