没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
In a round-oval-round pass rolling sequence, the cross-section profile of an outgoing workpiece was predicted first after getting the maximum spread. The concept “critical point on the contact boundary” was proposed and the coordinates of the critical poi
资源推荐
资源详情
资源评论

Journal of University of Science and Technology Beijing
Volume 15, Number 3, June 2008, Page 344
Materials
Corresponding author: Yonggang Dong, E-mail: d_peter@163.com Also available online at www.sciencedirect.com
© 2008 University of Science and Technology Beijing. All rights reserved.
An analytical model for the prediction of cross-section profile
and mean roll radius in alloy bar rolling
Yonggang Dong
1)
, Wenzhi Zhang
1)
, and Jianfeng Song
2)
1) School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China
2) School of Eletromechanical Engineering, Harbin Institute of Technology, Harbin 150001, China
(Received 2007-05-24)
Abstract: In a round-oval-round pass rolling sequence, the cross-section profile of an outgoing workpiece was predicted first after
getting the maximum spread. The concept “critical point on the contact boundary” was proposed and the coordinates of the critical
point were solved. The equivalent contact section area was represented and the mean roll radius was determined. The validity of this
model was examined by alloy bar rolling experiment and rigid-plastic FEM simulation. Compared with the existing models, the
mean roll radius obtained by this model is similar to experiment data.
© 2008 University of Science and Technology Beijing. All rights reserved.
Key words: alloy steel; critical point; cross-section profile; mean roll radius; round-oval-round
1. Introduction
In strip (or plate) rolling process, the calculation of
rolling speed by the multiplication of roll rpm and roll
radius is very simple. However, in rod (or bar) rolling
process, the roll surface is not smooth for the groove
on the roll, so the determination of rolling speed be-
comes difficult, as the roll radius is not constant along
the direction of roll axis. Consequently, for calculating
the rolling speed of the workpiece in the grooved roll,
the “mean roll radius” has been used as equivalent ra-
dius to replace the varying roll radius along the roll
groove profile.
For calculating the mean roll radius, the cross- sec-
tion profile of the outgoing workpiece should be pre-
dicted. Shinokura and Takai [1-3] presented an expe-
rimentally based model for the prediction of
cross-section profile in oval pass rolling. Kemp [4]
proposed a model for the prediction of cross-section
profile in oval and round groove rolling, but did not
represent the equation for the cross-section profile.
Kim[5
] represented a free surface scheme for the
analysis of plastic deformation in shape rolling.
For determining the mean radius of the grooved roll,
some calculating models were proposed by scholars.
This article studied the deformation law of the alloy
bar (or rod) in the groove, and the cross-section profile
of an outgoing workpiece has been predicted, and then
a novel model was proposed to calculate the mean roll
radius. The mean roll radius calculated by this was
compared with the existing models.
2. Prediction of cross-section profile of the
outgoing workpiece
According to the research of Lee [6-9], the free
surface profile at the exit cross-section can be ex-
pressed as a circular arc. As can be seen in Figs. 1 and
2, the radius of the circular arc is shown as
s
R
, and
the intersection between the free surface and the
groove curve is defined as “critical point on the con-
tact boundary”. So the cross-section profile can be
predicted when
s
R
and the critical point
,
YZ
CC
are
known. The coordinate of the critical point
,
YZ
CC
must be solved for the exact determination of
cross-section profile. Consequently, the model for
solving the critical point
,
YZ
CC
should also be built.
2.1
. Critical point in round-oval pass rolling
Once the groove profile and roll gap are known, the
position of the critical point
,
YZ
CC
can be just
determined by the maximum spread
b
or maximum
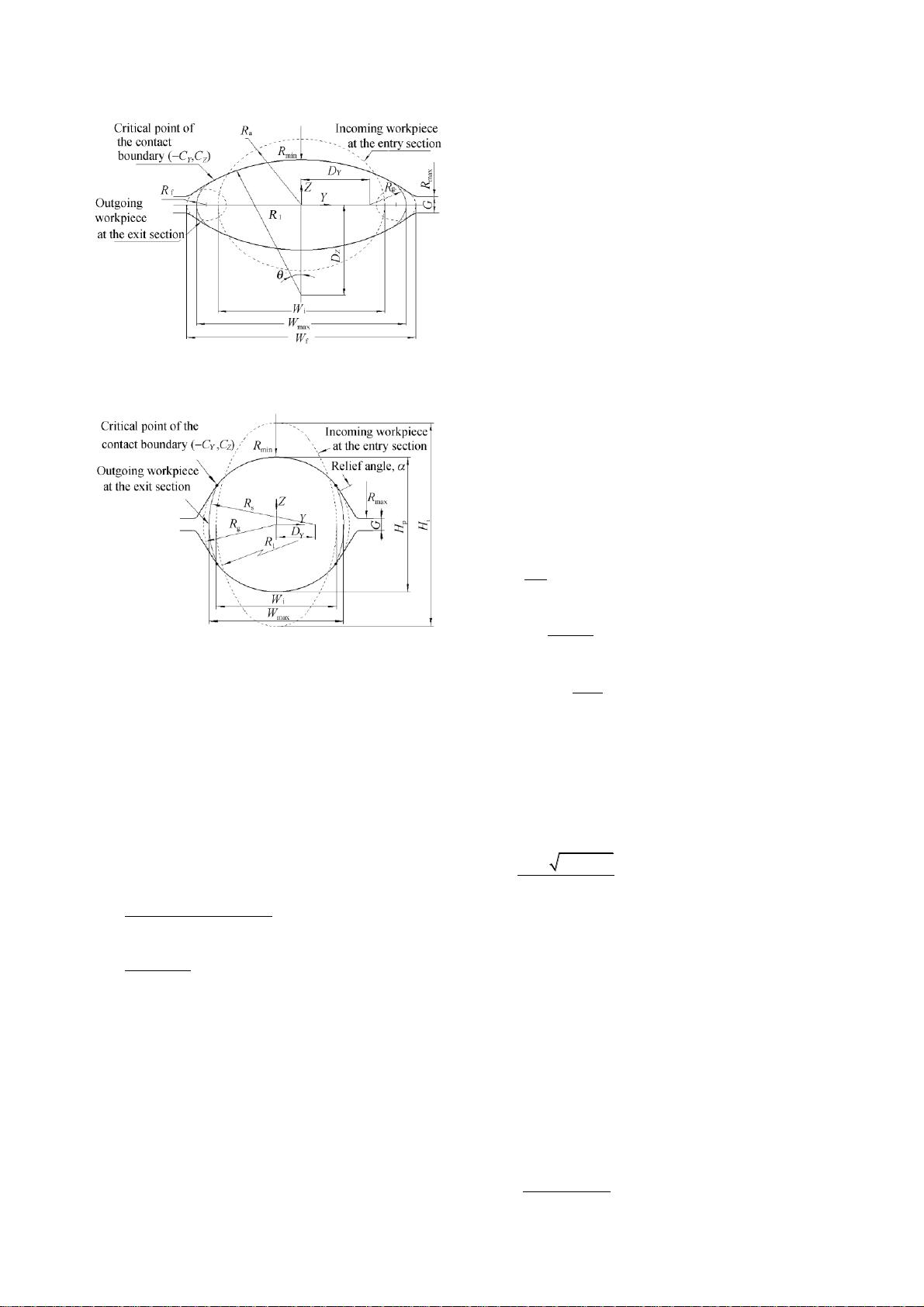
Y.G. Dong et al., An analytical model for the prediction of cross-section profile… 345
width
max
W
.
Fig. 1. Parameter designation of round-oval pass for
solving the critical point (C
Y
, C
Z
).
Fig. 2. Parameter designation of oval-round pass for
solving the critical point (C
Y
, C
Z
).
s
R
can be predicted as the linear interpolation of
a
R
and
f
R
( Fig. 1) or
1
R
and
g
R
( Fig. 2), once
max
W
is known.
max
W
is the maximum width of the
outgoing workpiece, which can be calculated by Shi-
nokura and Takai’s equation [3].
In round-oval pass rolling,
s
R
and
f
R
may be
given by
s a t f t
1R R W R W
(1)
22
1 p p
f
f
1f
/4
2
R H W H
R
RW
(2)
f max
t
fi
WW
W
WW
(3)
max i
W W b
(4)
where
a
R
is the radius of curvature of the incoming
cross-section.
t
W
a weighting function,
i
W
the
width of the inlet cross-section,
f
W
the width of the
roll groove area,
b
the maximum spread of the
outgoing workpiece.
The critical point
,
YZ
CC
, at which the oval
groove intersects the surface profile of the outgoing
workpiece, can be formulated as two simultaneous
circular equations:
2 2 2
s
()
YY
Z
C D C R
(5)
2 2 2
1
()
ZZ
Y
D C C R
(6)
where
Y
D
, the distance along the direction of Y-axis
between the origin coordinate and the center of the
arc
s
R
, is shown as
max s
2 /2
Y
D W R
(7)
where
z
D
, the distance along the direction of Z-axis
between the origin coordinate and the center of the arc
1
R
, is shown as
1p
/2
Z
D R H
(8)
where
1
R
is the radius of the oval groove ,
p
H
the
thickness of the roll groove area.
A new Eq. (9) can be obtained by Eqs. (5) and (6).
2
0
Z
Z
a C b C c
(9)
where
a
,
b
,
c
are shown , respectively, as
2
2
1
Z
Y
D
a
D
(10)
0
2
2
Z
Z
Y
kD
bD
D
(11)
2
0
22
1
2
4
Z
Y
k
c D R
D
(12)
where
0
k
is shown as
2 2 2 2
0s
1
YZ
k R D R D
(13)
Solving the simple binomial Eq. (9),
Z
C
can be
expressed explicitly in terms of
a
,
b
,
c
as
2
4
2
Z
b b ac
C
a
(14)
According to Eq. (14), two solutions of
Z
C
will
be obtained. However, in these two solutions, only
one is effective or available. In other words, one of
two solutions has to be excluded.
The reference point
00
,
YZ
CC
, at which the oval
groove intersects the surface profile of incoming
workpiece, can be formulated as
2 2 2
0
01
()
ZZ
Y
D C C R
(15)
2 2 2
0a
0
Z
Y
C C R
(16)
Solving Eqs. (15) and (16), yields
2 2 2
a
1
0
2
Z
Z
Z
RRD
C
D
(17)
剩余7页未读,继续阅读
资源评论

weixin_38698174
- 粉丝: 3
- 资源: 980
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功