BuildingaBw-TreeTakesMoreThanJustBuzzWords-2018(mod342-wangA)-计算机科学资源-CSDN文库

139 浏览量 2021-04-22 15:51:12 上传评论收藏 2.19MB PDF 举报

资源推荐

资源详情

资源评论

Building a Bw-Tree Takes More Than Just Buzz Words

Ziqi Wang

Carnegie Mellon University

ziqiw@cs.cmu.edu

Andrew Pavlo

Carnegie Mellon University

pavlo@cs.cmu.edu

Hyeontaek Lim

Carnegie Mellon University

hl@cs.cmu.edu

Viktor Leis

TU München

leis@in.tum.de

Huanchen Zhang

Carnegie Mellon University

huanche1@cs.cmu.edu

Michael Kaminsky

Intel Labs

michael.e.kaminsky@intel.com

David G. Andersen

Carnegie Mellon University

dga@cs.cmu.edu

ABSTRACT

In 2013, Microsoft Research proposed the Bw-Tree (humorously

termed the “Buzz Word Tree”), a lock-free index that provides high

throughput for transactional database workloads in SQL Server’s

Hekaton engine. The Bw-Tree avoids locks by appending delta

record to tree nodes and using an indirection layer that allows it to

atomically update physical pointers using compare-and-swap (CaS).

Correctly implementing this techniques requires careful attention

to detail. Unfortunately, the Bw-Tree papers from Microsoft are

missing important details and the source code has not been released.

This paper has two contributions: First, it is the missing guide

for how to build a lock-free Bw-Tree. We clarify missing points in

Microsoft’s original design documents and then present techniques

to improve the index’s performance. Although our focus here is on

the Bw-Tree, many of our methods apply more broadly to designing

and implementing future lock-free in-memory data structures. Our

experimental evaluation shows that our optimized variant achieves

1.1–2.5

better performance than the original Microsoft proposal

for highly concurrent workloads. Second, our evaluation shows

that despite our improvements, the Bw-Tree still does not perform

as well as other concurrent data structures that use locks.

ACM Reference Format:

Ziqi Wang, Andrew Pavlo, Hyeontaek Lim, Viktor Leis, Huanchen Zhang,

Michael Kaminsky, and David G. Andersen. 2018. Building a Bw-Tree Takes

More Than Just Buzz Words. In Proceedings of 2018 International Conference

on Management of Data (SIGMOD’18) . ACM, New York, NY, USA, 16 pages.

https://doi.org/10.1145/3183713.3196895

1 INTRODUCTION

Lock-free data structures are touted as being ideal for today’s multi-

core CPUs. They are, however, notoriously dicult to implement

for several reasons [

]. First, writing ecient and robust lock-free

code requires the developer to gure out all possible race conditions,

the interactions between which can be complex. Furthermore, The

point that concurrent threads synchronize with each other are

In this the paper, we always use the term “lock” when referring to “latch”.

Permission to make digital or hard copies of all or part of this work for personal or

classroom use is granted without fee provided that copies are not made or distributed

for prot or commercial advantage and that copies bear this notice and the full citation

on the rst page. Copyrights for components of this work owned by others than ACM

must be honored. Abstracting with credit is permitted. To copy otherwise, or republish,

to post on servers or to redistribute to lists, requires prior specic permission and/or a

fee. Request permissions from permissions@acm.org.

SIGMOD’18, June 10–15, 2018, Houston, TX, USA

ACM ISBN 978-1-4503-4703-7/18/06.. . $15.00

https://doi.org/10.1145/3183713.3196895

usually not explicitly stated in the serial version of the algorithm.

Programmers often implement lock-free algorithms incorrectly

and end up with busy-waiting loops. Another challenge is that

lock-free data structures require safe memory reclamation that is

delayed until all readers are nished with the data. Finally, atomic

primitives can be a performance bottleneck themselves if they are

used carelessly.

One example of a lock-free data structure is the Bw-Tree from

Microsoft Research [

]. The high-level idea of the Bw-Tree is

that it avoids locks by using an indirection layer that maps logical

identiers to physical pointers for the tree’s internal components.

Threads then apply concurrent updates to a tree node by appending

delta records to that node’s modication log. Subsequent operations

on that node must replay these deltas to obtain its current state.

The indirection layer and delta records provide two benets.

First, it avoids coherence trac of locks by decomposing every

global state change into atomic steps. Second, it incurs fewer cache

invalidations on a multi-core CPU because threads append delta

records to make changes to the index instead of overwriting exist-

ing nodes. The original Bw-Tree paper [

] claims that this lower

synchronization and cache coherence overhead provides better

scalability than lock-based indexes.

To the best of our knowledge, however, there is no comprehen-

sive evaluation of the Bw-Tree. The original paper lacks detailed

descriptions of critical components and runtime operations. For

example, they do not provide a scalable solution for safe memory

reclamation or ecient iteration. Microsoft’s Bw-Tree may support

these features, but the implementation details are unknown. This

paper aims to be a more thorough investigation of the Bw-Tree: to

supply the missing details, propose improvements, and to provide

a more comprehensive evaluation of the index.

Our rst contribution is a complete design for how to build an

in-memory Bw-Tree. We present the missing features required for a

correct implementation, including important corner cases missing

from the original description of the data structure. We then present

several additional enhancements and optimizations that improve

the index’s performance. The culmination of this eort is our open-

source version called the

OpenBw-Tree

. Our experiments show

that the OpenBw-Tree outperforms what we understand to be the

original Bw-Tree design by 1.1–2.5

for insert-heavy workloads

and by 1.1–1.4× for read-heavy workloads.

Our second contribution is to compare the OpenBw-Tree against

four other state-of-the-art in-memory data structures: (1) SkipList [

(2) Masstree [

], (3) a B+Tree with optimistic lock coupling [

]

and (4) ART [

] with optimistic lock coupling [

]. Our results

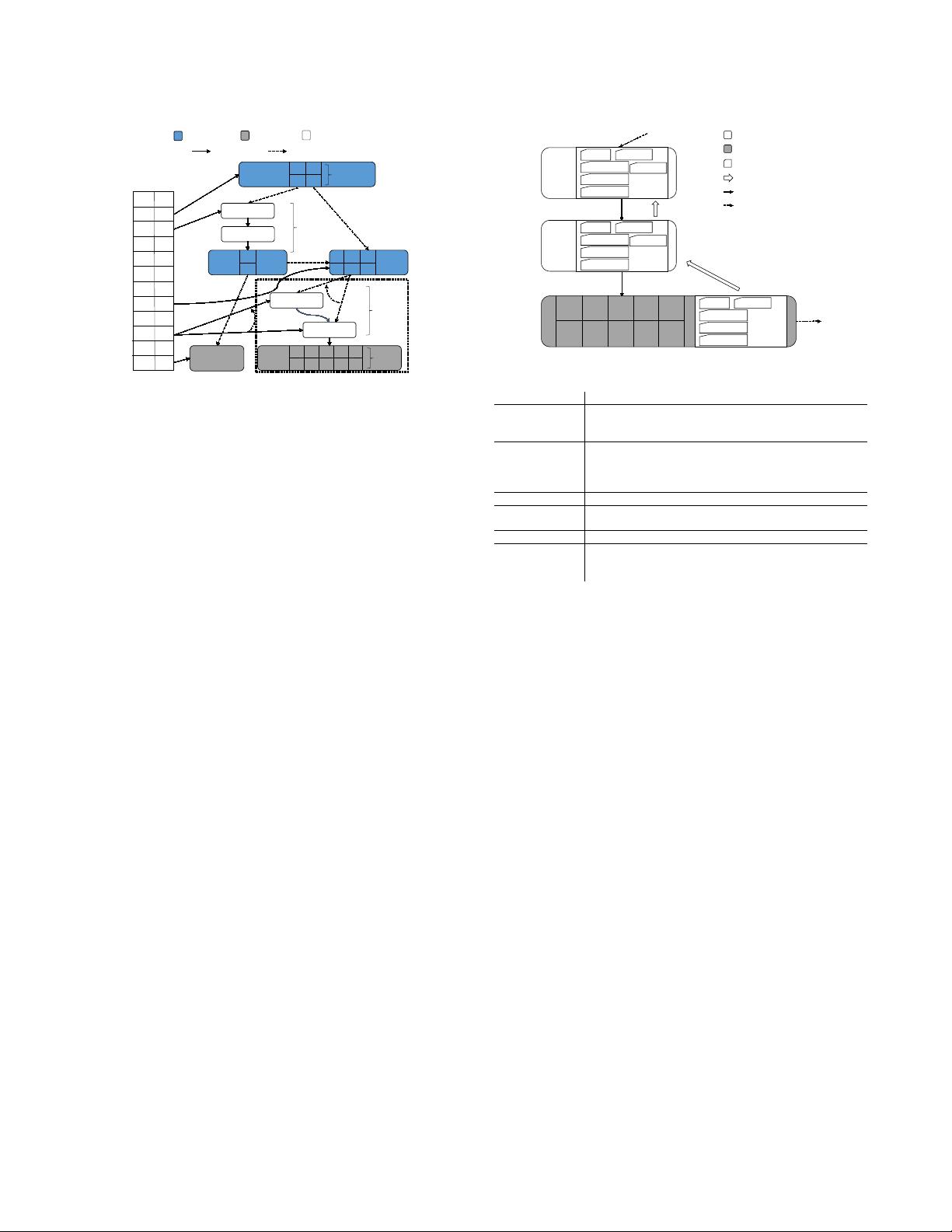
Inner

Mapping

Table

Inner

Delta

Chain

Leaf

Delta

Chain

Leaf

Inner node

Physical link Logical link

Delta node

Leaf node

new

CaS

old

Ptr

Separator

items

Data

items

Leaf

Figure 1: Architecture Overview

– An instance of a Bw-Tree with its

internal logical links, Mapping Table links, and an ongoing CaS operation

on the leaf Delta Chain.

show that despite previous claims of lock-free indexes being su-

perior to lock-based indexes on multi-core CPUs, the overhead

of the Bw-Tree’s indirection layer and delta records causes it to

under-perform the lock-based indexes by 1.5–4.5×.

2 BW-TREE ESSENTIALS

Although the Bw-Tree has been covered in previous papers [

–

], additional details are needed to understand our discussion in

Sections 3 and 4. We assume that the Bw-Tree is deployed inside

of a database management system (DBMS) with a thread pool, and

has worker threads accessing the index to process queries. If non-

cooperative garbage collection is used, the DBMS also launches

one or more background threads periodically to perform garbage

collection on the index.

The most prominent dierence between the Bw-Tree and other

B+Tree-based indexes is that the Bw-Tree avoids directly editing

tree nodes because it causes cache line invalidation. Instead, it stores

modications to a node in a delta record (e.g., insert, update, delete),

and maintains a chain of such records for every node in the tree.

This per-node structure, called a Delta Chain, allows the Bw-Tree

to perform atomic updates via CaS. The Mapping Table serves as

an indirection layer that maps logical node IDs to physical pointers,

making atomic updates of several references to a tree node possible.

The mapping table works as follows: As shown in Fig. 1, every

node in the Bw-Tree has a unique logical node ID (64-bit). Instead of

using pointers, nodes refer to other nodes using these IDs (logical

links). When a thread needs the physical location of a node, it

consults the Mapping Table to translate a node ID to its memory

address. Thus, the Mapping Table allows threads to atomically

change the physical location of a node without having to acquire

locks: a single atomic compare-and-swap (CaS) instruction changes

multiple logical links to a node throughout the index.

2.1 Base Nodes and Delta Chains

A logical node (called “virtual node” in [

]) in the Bw-Tree has

two components: a base node and a Delta Chain. There are two

types of base nodes: an inner base node that holds a sorted (key,

node ID) array, and a leaf base node that holds a sorted (key, value)

Size: 5

Low Key: K

High Key: K

Right Sib: N

To N

Depth: 0

From Parent

Attribute

Delta node

Leaf Node

Attr. Entry

Attr. Inheritance

Physical link

Logical link

Δdelete

, V

]

Size: 4

Low Key: K

High Key: K

Right Sib: N

Depth: 1

Attribute

Δinsert

, V

]

Size: 5

Low Key: K

High Key: K

Right Sib: N

Depth: 2

Attribute

Offset: 1

Offset: 0

Figure 2: Delta Records Overview

– A more detailed illustration of a

logical leaf node from Fig. 1 with its base node and two delta nodes.

Attribute Description

low-key

The smallest key stored at the logical node. In a node split, the

low-key of the right sibling is set to the split key. Otherwise, it

is inherited from the element’s predecessor.

high-key

The smallest key of a logical node’s right sibling.

∆split

records

use the split key for this attribute.

∆merge

records use the

high-key of the right branch. Otherwise, it is inherited from the

element’s predecessor.

right-sibling The ID of the logical node’s right sibling.

size

The number of items in the logical node. It is incremented for

∆insert records and decremented for ∆delete records.

depth The number of records in the logical node’s Delta Chain.

oset

The location of the inserted or deleted item in the base node if

they were applied to the base node. Only valid for

∆insert

and

∆delete records.

Table 1: Node Attributes

– The list of the attributes that are stored in the

logical node’s elements (i.e., base node or delta records).

array. Initially, the Bw-Tree consists of two nodes, an empty leaf

base node, and an inner base node that contains one separator item

referring to the empty leaf node. Base nodes are immutable.

As shown in Fig. 2, a Delta Chain is a singly linked list that

contains a chronologically-ordered history of the modications

made to the base node. The entries in the Delta Chain are connected

using physical pointers, with the tail pointing to the base node. Both

the base node and its delta records contain additional meta-data

that represent the state of the logical node at that point in time (see

Table 1). That is, when a worker thread updates a logical node, they

compute the latest attributes of the logical node and store them

in the delta record. The threads then use this information when

navigating the tree or when performing structural modications to

avoid having to traverse (and replay) a node’s Delta Chain.

As we next describe, a node’s logical link in the Mapping Table

points to either a Delta Chain entry or the base node. Threads

append new entries to the head of a node’s Delta Chain and then

update the physical address in the Mapping Table.

2.2 Mapping Table

The Bw-Tree borrows the B

link

-Tree design where a node can have

two inbound pointers, one from the parent and one from the left

sibling [

]. Updating these pointers atomically requires either

hardware support (e.g., transactional memory [

]) or complex

software primitives (e.g., multi-word CaS [2, 12, 14]).

The Bw-Tree’s centralized Mapping Table avoids these problems

and allows a thread to update all references to a node in a single CaS

instruction that is available on all modern CPUs. If a thread’s CaS

fails then it aborts its operation and restarts. This restart is transpar-

ent to the higher-level DBMS components. Threads always restart

an operation by traversing again from the tree’s root. Although

more sophisticated restart protocols are possible (e.g., restarting

from the previous level in the tree), we contend that restarting from

the root simplies the implementation. The nodes that a thread will

revisit after a restart will likely be in the CPU cache anyway.

Although this paper focuses only on in-memory behavior of the

Bw-Tree, it is worth emphasizing that the mapping table also serves

the purpose of supporting log-structured updates when deployed

with SSD. Updates to tree nodes will otherwise propagate to all

levels without the extra indirection provided by the Mapping Table.

2.3 Consolidation and Garbage Collection

As we described above, worker threads update the Bw-Tree by

appending new delta records to the logical nodes’ Delta Chains.

This means that these Delta Chains are continually growing, which

in turn increases the time that it takes for threads to traverse the

tree because they must replay the delta records to get the current

state of a logical node. To prevent excessively long Delta Chains,

worker threads will periodically consolidate a logical node’s delta

records into a new base node. Consolidation is triggered when Delta

Chain’s length exceeds some threshold. Microsoft reported that a

length of eight was a good setting [

]. Our results in Section 5.3

show that using dierent thresholds for inner nodes versus leaf

nodes yields the best performance.

At the beginning of consolidation, the thread copies the logical

node’s base node contents to its private memory and then applies

the Delta Chain. It then updates the node’s logical link in the Map-

ping Table with the new base node. After consolidation, the index

reclaims the old base node and Delta Chain memory after all other

threads in the system are nished accessing them. The original

Bw-Tree uses a centralized epoch-based garbage collection scheme

to determine when it is safe to reclaim memory [25].

2.4 Structural Modication

As with a B+Tree, a Bw-Tree’s logical node is subject to overow

or underow. These cases require

splitting

a logical node with too

many items into two separate nodes or

merging

together under-

full nodes into a new node. We briey describe the Bw-Tree’s struc-

tural modication (SMO) protocols for handling node splits and

merges without using locks. The main idea is to use special delta

records to represent internal structural modications.

The SMO operation is divided into two phases: a logical phase

which appends special deltas to notify other threads of an ongoing

SMO, and a physical phase which actually performs the SMO. In

the logical phase, some thread t appends a

∆insert

∆merge

∆remove

to the virtual node, updating its attributes such as the

high key and next node ID. The updated attributes guarantee that

other worker threads always observe consistent virtual node states

during their traversal. In the following physical phase, t’ (not nec-

essarily the same thread as t) will split or merge the node, and then

replace the old virtual node with the new node via CaS.

Although the Bw-Tree is lock-free, threads are not guaranteed

to make progress because of failed CaS. One way to alleviate this

starvation is for threads to cooperatively complete a multi-stage

SMO, which in known as the help-along protocol [

]. Threads must

help complete an unnished SMO before the corresponding virtual

node can be traversed.

3 MISSING COMPONENTS

This section introduces our design and implementation of four

components that are either missing or lacking details from the Bw-

Tree papers. Since we assume that the Bw-Tree will be used in a

DBMS, in Section 3.1 we also describe how to support non-unique

keys, followed by iterators in Section 3.2. Finally, we discuss how

to enable dynamic Mapping Table expansion in Section 3.3.

3.1 Non-unique Key Support

During traversal, Bw-Tree stops at the rst leaf delta record that

matches the search key, without continuing down the chain. This

behavior, however, is incompatible with non-unique key support.

We handle non-unique keys in the OpenBw-Tree by having

threads compute the visibility of delta records on-the-y using

two disjoint value sets for a search key, as shown in Fig. 3. The

rst set (

present

) contains the values that are already known to

be present. The second set (

deleted

) contains the values that are

known to be deleted. While traversing the leaf Delta Chain, if a

worker thread nds an insert delta record with key

and value

where

V < S

deleted

, it adds

present

. If the thread nds a delete

delta record with key

and value

where

K < S

present

, it adds

deleted

. Update deltas are processed as a delete delta of the old

value followed by an insert delta of the updated value. Although

we largely ignore update deltas in the discussion, they are posted

when a worker thread modies a key-value pair. After reaching

the base node with values for

, denoted

base

, the thread returns

present

∪ (S

base

− S

deleted

)

as the values of

. This result returns

all values whose existence has not been overridden by any earlier

delta records in the Delta Chain.

Computing

present

and

deleted

is inexpensive, and is performed

only when traversing a leaf node’s Delta Chain. A delta record may

insert only one value to either set. Because the max chain length is

typically small and xed (e.g., 24 [

]), OpenBw-Tree stack allocates

present

and S

deleted

as two variable-length arrays.

3.2 Iteration

To support range scans on an index, the DBMS’s execution engine

uses an iterator. This interface is complex to implement in the Bw-

Tree since it must support concurrent operations without locks.

Tracking a thread’s current location in an iterator is dicult when

other threads are simultaneously inserting and deleting items. Fur-

thermore, concurrent SMOs (Section 2.4) make it more challenging

when the iterator moves from one logical leaf node to its neighbor.

To overcome these problems, OpenBw-Tree’s iterator does not

operate directly on tree nodes. Instead, each iterator maintains a

private, read-only copy of a logical node that enables consistent

and fast random access. The iterator also maintains an oset of the

current item in this node, as well as information for determining

the next item. As the iterator moves forward or backward, if the

current private copy has been exhausted, the worker thread starts

剩余15页未读，继续阅读

评论收藏

内容反馈

weixin_38696458

粉丝: 5
资源: 919

Building a Bw-Tree Takes More Than Just Buzz Words - 2018 (mod34...

最新资源

Building a Bw-Tree Takes More Than Just Buzz Words - 2018 (mod34...

buzz语音生成，抖音，B站等网站语音合成

Buzz-0.8.3-windows.exe

c语言-leetcode题解412-fizz-buzz.c

fizz-buzz-java:Fizz Buzz kata的源代码。 视频在

PyPI 官网下载 | py-buzz-1.0.1.tar.gz

github-actions-fizz-buzz

which-more-buzz

buzz_Buzz_speaker_windows_

C++-leetcode题解之412-Fizz-Buzz.cpp

Python库 | django-buzz-0.4b.tar.gz

Buzz.MVC-开源

fizz-buzz-python:Jeu Fizz Buzz en Python

LeetCode最全代码

kata2TDD-FizzBuzz:Kata TDD - 持续集成 - Fizz Buzz

htc 手机 读取BUZZ版本信息的 revolutionary-0.4pre4

Algorithm-implementation-in-JS---part-1

fizz-buzz

GirlsDay Buzz桌面主题

三协 Robot sankyo 5000SPwin Buzz

Buzz-Mod-v12

PyPI 官网下载 | buzz_agent-1.1.7.tar.gz

Python库 | flask-buzz-0.1.13.tar.gz

haxe-buzz:Buzz for Haxe的外部功能

Buzz-0.7.1-windows 是一款免费的音乐制作软件

game-of-fizz-buzz:FizzBu​​zz的简单游戏

Buzz：PHP的轻量级HTTP客户端

[2018] Elm for Web Development.(Ajdin Imsirovic).[1788299051]

fizz-buzz:Fizz Buzz 游戏的 Groovy 实现

fizz-buzz-lab

最新资源

fizz-buzz-java:Fizz Buzz kata的源代码。视频在

htc 手机读取BUZZ版本信息的 revolutionary-0.4pre4

game-of-fizz-buzz:FizzBuzz的简单游戏