收稿日期:2002-06-06;修改稿收到日期:2 00 3-07-18.
基金项目:国家自然科学基金重点项目基金(501391010);面
上基金(50279001);大连理工大学海岸和近海工
程国家重点实验室访问学者基金资助项目 .
作者简介:王 哲
*
(1961-),男,博士,副研究员 .
林 皋 (1929-),男, 中 科 院院 士 .
第21卷第2期
2004 年 4 月
计算力学学报
Chinese Jour nal of Computational M echanics
Vol
.21,
No
.2
April
2004
文章编号:1007-4708(2004)02-0231-06
无耦合条件下的多子系统静动态统一本构关系(下 )
—— 铝的双子系统静动态统一本构模型
王 哲
*1,2
, 林 皋
3
(1. 北京交通大学 土建学院,北京 100044;2.大连理工大学 海岸和近海工程国家重点实验室,大连 116024;
3. 大连理工大学 土建学院,大连 116024)
摘 要:构造了标量形式的无耦合条件下双子系统静动态统一本构模型。推导出第 1 和第 2 子系统中加载应变
速率临界值
ε
·
c1
和
ε
·
c2
,当应变速率
ε
·
分别低于和高于某个临界值时,相应子系统中的不可逆行为分别是与时间无
关的和与时间相关的。由于当
ε
·
跨越
ε
·
c 1
和
ε
·
c2
时,内变量的求解公式发生变化,所以动态强度随
ε
·
变化的规律发
生变化。经与铝的实验结果比较确认,本构模型能够描述材料的多种静动态力学行为。
关键词:本构模型;铝;静态;动态
中图分类号:
O
344 文献标识码:
A
1 引 言
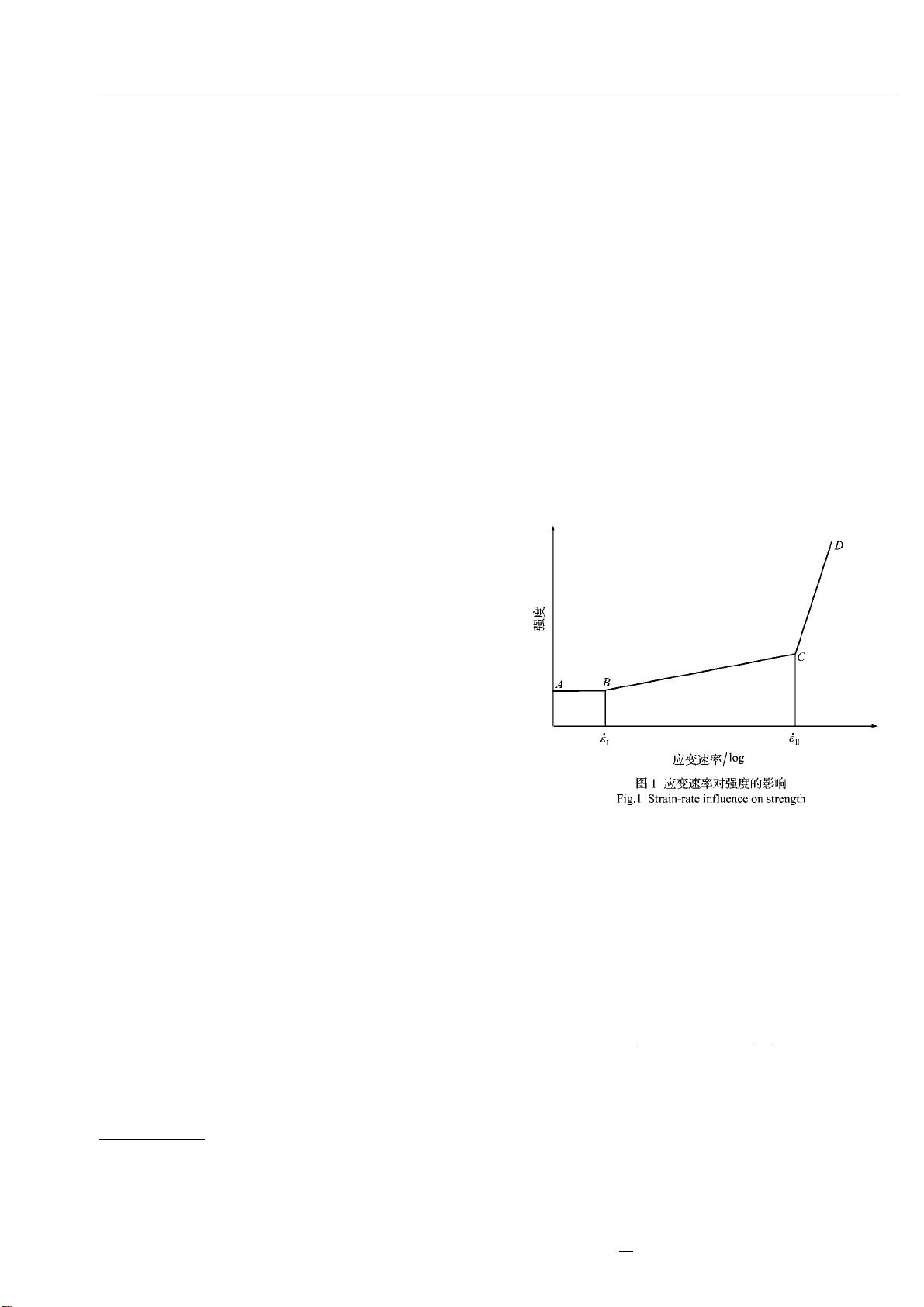
分析文献[1-5] 的实验数据认为,存在有两个
应变速率的临界值,ε
·
Ⅰ
和ε
·
Ⅱ
(ε
·
Ⅱ
>ε
·
Ⅰ
), 当加 载应
变速率 ε
·
满足 0 < ε
·
<ε
·
Ⅰ
时,材料的强度不随 ε
·
变
化;当满足 ε
·
Ⅰ
<ε
·
<ε
·
Ⅱ
时,强度随 ε
·
的增加而缓慢
增加;当 满足 ε
·
>ε
·
Ⅱ
时,强度随 ε
·
的增加而急剧增
加。这些文献中没有刻意强调 ε
·
Ⅰ
的存在,通常认
为,加载应变速率低于 10
-4
/s 或 10
-5
/s 时,材料强
度就不再随应变速率变化。因此,没有再给出应变
速率低于 10
-5
/s 时强度的实验值。
汇总以上的分析认为,材料的强度与应变速率
之间关系可由图 1来描述,其中 AB 段与横轴平行。
本文将严格遵循文献[6] 提供的理论规则来
构造铝的双子系统标量本构模型,并将对图 1 描述
的现象进行解释。由于本文所依据的理论是新提出
的,所建模型将与现有文献中的模型有较大区别。
2 模型构造
现有文献报道高速冲击实验时,提供的实验数
据几乎都不完整,例如本文后面引用的文献只给出
了剪应力与剪应变的数据。
由于得不到应力的所有
分量和应变的所有分量,无法把实验结果与张量形
式的本构模型的计算结果进行比较。因此,本文只
构造标量形式的本构模型。
另外,限定材料变形满足小变形假设。
2.1 Helmoholtz 自由能及内变量演化方程
对于具有图 1 性质的这类材料,我们用双子系
统本构关系进行描述。构造 H elm ohltz 自由能为
ψ=
∑
2
i =1
A
i
1
2
ε
2
- B
i
ε·q
i
+
1
2
C
i
q
2
i
- H
i
p
i
其中 ε为应变,q
i
和 p
i
为内变量,A
i
,B
i
,C
i
和 H
i
为
取正值的材料常数,所有符号中下角标 i 均代表子
系统的序号(相当于文献[6]3.2 节之后的上角标
ξ),i 的 取值范围是 1 和 2。按照文献[6] 的式(2,3)
对 ψ求偏导,有
σ=
ψ
ε
=
∑
2
i=1
A
i
(ε- B
i
q
i
)(1)
资源评论
weixin_38695471
- 粉丝: 3
- 资源: 911
最新资源
- 打卡没事，等你打完看到吗水浇地
- 电力变压器中的故障分析数据集
- 车载软件平台：面向未来的新型ADAS架构推动零事故愿景
- pytorch实现基于LSTM的高速公路车辆轨迹预测源码+数据集+说明（高分项目）
- pytorch实现基于LSTM的高速公路车辆轨迹预测源码+数据集+说明
- Java 飞机订票系统实训报告
- 教育领域的新年主题环创：从幼儿园到中学的创意布置与新年活动设计
- 智能小车路径规划 算法：RRT与Dubins相结合的方法，混合A*与Dubins相结合的方法 实现智能小车最短路径规划
- 枸杞虫害图像分类数据集【已标注，约9,000张数据】
- 基于Python（tkinter）+sqlite3的图书信息管理系统源码+数据库（高分课程设计）
- FOC+SMO+PLL的Simlink仿真模型
- 基于Java 和MySQL的飞机订票系统
- 信号处理辅助软件课程设计报告 信号处理辅助软件中GUIDE工具的计算器和绘图程序的设计与实现
- OpenCV计算机视觉基础 ppt（非教材自带ppt）
- 三相异步电机矢量控制仿真模型
- 多模态应用-基于BERT+ResNet的多种融合方式实现多模态的情感分析源码（高分大作业&课设）
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
