Aperformance-drivenmulti-algorithmselectionstrategyforenergyconsumptionoptimizationofsea-railintermodaltransportation资源-CSDN文库

183 浏览量 2021-02-08 19:00:07 上传评论收藏 2.3MB PDF 举报

A performance-driven multi-algorithm selection strategy for energy consumption optimization of sea-rail intermodal transportation 标题《A performance-driven multi-algorithm selection strategy for energy consumption optimization of sea-rail intermodal transportation》和描述中提到的关键词和概念主要集中在差分进化算法、多算法选择策略、海铁联运、能源消耗优化等几个方面。本文深入探讨了如何通过性能驱动的多算法选择策略（PMSS）来优化海铁联运能源消耗问题。为了全面解读这个研究话题，我们可以从以下几个知识点进行详细阐述： 1. 差分进化算法（Differential Evolution，DE）：差分进化算法是一种简单高效的全局优化算法，它属于进化算法的一种，特别适合解决连续空间优化问题。DE算法通过在种群中的个体之间进行差分操作，产生新的候选解，并以一定的策略与当前种群中的个体竞争，从而实现进化。过去几年中，多种强大的DE算法被开发出来，但由于不同算法在不同类型的优化问题上的表现各异，因此没有一种DE算法能够始终保持最优性能。 2. 多算法选择策略：在解决现实世界的复杂问题时，选择一个合适的算法并不容易。问题的属性通常事先并不完全了解，因此自动选择一个适当的算法版本来解决特定问题是一项重要且具有挑战性的任务。多算法选择策略是为了解决这一问题而提出的，旨在通过某种机制自动地从一系列算法中选择最适合当前问题的算法。 3. 学习-遗忘机制：在提出的性能驱动多算法选择策略（PMSS）中，引入了学习-遗忘机制来更新算法选择概率，以确保在搜索过程中选择性能最佳的算法。这种机制允许算法在解决问题的过程中学习哪些算法表现得更好，并在后续的迭代中遗忘表现不佳的算法，从而保持整个算法池的动态优化。 4. 单目标优化问题： PMSS策略主要针对的是单目标优化问题，这类问题的目标是寻找一个解，使得单一的目标函数达到最优值。由于这类问题的复杂性和多样性，采用单一算法往往难以找到全局最优解，因此需要一种能够根据问题特性动态选择算法的机制。 5. 海铁联运能源消耗优化：海铁联运是一种利用海洋和铁路两种运输方式相结合的多式联运模式。该模式相比单一运输方式具有成本节约、运输时间缩短、安全性提高等优势。能源消耗优化是海铁联运中需要特别关注的问题，因为运输系统的能源效率直接影响到运输成本和环境影响。在本文中，PMSS策略被应用于海铁联运的能源消耗优化中，旨在实现运输过程中的能效提升。 6. 测试问题和模拟结果：为了验证PMSS策略的有效性和计算效率，本文采用了两套广泛使用的测试问题集进行测试，结果表明PMSS策略在解决单目标优化问题时非常有效。PMSS被用于海铁联运能源消耗的优化中，模拟结果证明了该算法能够成功找到满意的解决方案，并为问题和算法提供了深刻的见解，显示出其在实际应用中解决问题的巨大潜力。 7. 文章发表情况：本研究论文发表于《Swarmand Evolutionary Computation》期刊上，文章的作者来自上海海事大学物流研究中心、萨里大学计算机科学系以及华东理工大学控制科学与工程部。文章的发表表明了该研究成果的学术价值和科学贡献，为后续相关领域的研究提供了理论基础和实践指导。文章通过提出性能驱动的多算法选择策略，成功地将进化计算中的差分进化算法应用于海铁联运能源消耗优化问题。研究不仅为优化运输效率提供了新的技术路径，也为多目标优化问题提供了一种有效的解决框架。通过模拟测试和实证研究，展现了该策略在实际应用中的可行性和优越性。

资源推荐

资源详情

资源评论

A performance-driven multi-algorithm selection strategy for energy

consumption optimization of sea-rail intermodal transportation

Qinqin Fan

, Yaochu Jin

, Weili Wang

, Xuefeng Yan

Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China

Department of Computer Science, University of Surrey, Guildford, Surrey, GU2 7XH, United Kingdom

Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education, East China University of Science and Technology, Shanghai

200237, China

ARTICLE INFO

Keywords:

Differential evolution

Multi-algorithm selection

Sea-rail intermodal transportation

Energy consumption optimization

ABSTRACT

Various powerful differential evolution (DE) algorithms have been developed in the past years, although none of

them can consistently perform well on all types of problems. However, it is not straightforward to choose an

appropriate algorithm for solving a real-world problem, as the properties of the problem are usually not well

understood beforehand. Therefore, how to automatically select an appropriate DE variant for solving a particular

problem at hand is an important and challenging task. In the present work, a performance-driven multi-algorithm

selection strategy (PMSS) is proposed to alleviate the above mentioned problems for single objective optimization.

In PMSS, a learning-forgetting mechanism is introduced to update the selection probability of each algorithm from

a pool of DE variants to make sure that the best performing one is chosen during the search process. The effec-

tiveness of PMSS is carefully examined on two suites of widely used test problems and the results indicate that the

PMSS is highly effective and computationally efﬁcient. Finally, the proposed algorithm is employed to optimize

the energy consumption of sea-rail intermodal transportation. Our simulation results demonstrate that the pro-

posed algorithm is successful achieving satisfactory solution that are able to provide insights into the problem and

the algorithm is promising to be applied for solving real sea-rail intermodal and other multimodal transportation

planning problems.

1. Introduction

Over the past decades, a large number of meta-heuristic optimization

algorithms, which are inspired from the evolutionary process and swarm

behaviors in the nature [1], have been introduced and utilized to suc-

cessfully solve a wide range of industrial application optimization

problems. Among the family of meta-heuristic algorithms, differential

evolution (DE) [2], particle swarm optimization (PSO) [3], genetic al-

gorithm (GA) [4], estimation of distribution algorithm (EDA) [5], ant

colony optimization (ACO) [6], and covariance matrix adaptation evo-

lution strategy (CMA-ES) [7] are among the most popular ones. Ac-

cording to [8], meta-heuristic optimization algorithms can be generally

categorized into distributed and centralized models.

DE is one of the most popular paradigms of meta-heuristic algorithms

since it is a simple yet efﬁcient search technique. However, the perfor-

mance of DE heavily depends on its control parameters (i.e., mutation

control parameter F, crossover control parameter CR, and population size

NP) and strategies (i.e., mutation and crossover), especially when the

complexity of optimization problem is high [9]. To enhance the search-

ing performance of DE, researchers proposed numerous DE variants.

However, most existing studies focused on the ensemble of production

operators and/or tuning of control parameters. Although a number of

advanced DE variants have been developed to solve various practical

applications and benchmark problems, no single DE variant has been

shown to be able to consistently perform well on various types of opti-

mization problems, even if multi-operator search strategies or a combi-

nation of multi-parameters are used. Generally speaking, this is in

accordance with the no free lunch (NFL) theorem [10]. To alleviate the

NFL problem, some self-adaptive multi-algorithm selection mechanisms

have been developed. For Example, Vrugt et al. [11] proposed a

multi-algorithm genetically method for single-objective optimization

(AMALGAM-SO), which can automatically adjust the number of offspring

of each individual algorithm based on the current performance. Peng

et al. [12] introduced a population-based algorithm porfolio (PAP)

* Corresponding author. NO. 1550 Haigang Avenue, Shanghai 201306, PR China. Tel.: þ86 21 38284613.

E-mail addresses: forever123fan@163.com (Q. Fan), yaochu.jin@surrey.ac.uk (Y. Jin), weili.wang87@hotmail.com (W. Wang), xfyan@ecust.edu.cn (X. Yan).

Contents lists available at ScienceDirect

Swarm and Evolutionary Computation

journal homepage: www.elsevier.com/locate/swevo

https://doi.org/10.1016/j.swevo.2018.11.007

Received 3 February 2018; Received in revised form 8 September 2018; Accepted 22 November 2018

Available online 28 November 2018

Swarm and Evolutionary Computation 44 (2019) 1–17

wherein a part of given computational resources are used to evaluate the

performance of each constitute algorithm and a migration scheme is

employed to encourage interaction among individual algorithms. Yuen

et al. [13] proposed a multiple evolutionary algorithm, in which each

individual algorithm runs independently with no information exchange

and the best performance algorithm recommended by a novel online

performance prediction metric is used to generate new individuals.

Recently, Fan et al. [14] introduced an auto-selection mechanism (ASM),

in which a learning strategy and an additional selection probability are

used to update a select probability of each individual algorithm and

alleviate a greedy selection issue. The main target of these methods is to

automatically choose an appropriate algorithm in solving a given prob-

lem. Indeed, self-adaptive multi-algorithm is an effective way to address

the shortcomings of each single algorithm. However, the following lim-

itations exist in the above approaches when implemented in real appli-

cations. Firstly, information exchange is usually needed among the

algorithms to be selected [11,12]. Unfortunately, the results reported in

Ref. [13] and our experimental results imply that such information ex-

change may mislead the selection since each algorithm may have its own

particular search behavior. Secondly, a greedy selection strategy

[11–13], which increases the risk of wrong selections, is used to choose

an algorithm. Lastly, the selection is based on the predicted performance

[13], making it less reliable in practical applications, and ASM is a

“either/or” strategy [14].

To deal with the above mentioned limitations, a performance-driven

multi-algorithm selection strategy (PMSS) is proposed in this paper. In

PMSS, a learning-forgetting mechanism is developed to implement self-

adaptive selection of DE variants. The learning operator updates the se-

lection probability of each algorithm in each generation, while the

forgetting operator aims to reduce the risk of incorrect selections.

Moreover, no information exchange is needed among the algorithms in

the pool. It should be pointed out that this work does not mean to

improve the performance of a single existing DE variant; rather, it aims to

introduce a novel strategy (i.e., PMSS) to select a suitable DE variant for

solving different types of optimization problems. In this study, novel DE

(JADE) [15], ensemble of mutation strategies and control parameters

with DE (EPSDE) [16], and DE with self-adaptive strategy and control

parameters (SSCPDE) [17] are chosen as the algorithms to be selected in

the pool. In JADE, the mutation control parameter F is produced by a

Cauchy distribution C(

, 0.1), the crossover control parameter CR is

generated by a normal distribution function N(

, 0.1). Moreover, an

improved current-to-best/1 mutation strategy (called as current-to-pb-

est/1) is used in JADE. In EPSDE, three distinct performance mutation

strategies are selected in a pool. CR in pool varies from 0.1 to 0.9 with a

step equal to 0.1 and F in pool is taken in the range 0.4–0.9 with a step

equal to 0.1. Moreover, the selection of mutation strategy and control

parameters in EPSDE is based on their previous successful experience. In

SSCPDE, each individual has own control parameters (i.e., F and CR) and

mutation strategy. The control parameters F and CR are produced by a

normal distribution function in which a weighted average value is used

as a location parameter. Moreover, appropriate mutation strategies can

be self-adaptively selected from a strategy pool. Additionally, the per-

formances of all algorithms are evaluated in terms of the average ranking

according to the Friedman's test [18]. The performance of the proposed

algorithm is compared with that of JADE, EPSDE, SSCPDE, and a few

other state-of-the-art DE variants on two sets of 30- and 50-dimensional

test functions introduced in IEEE CEC2005 [19] and BBOB2012 [20].

PMSS is also compared with two multi-algorithm selection strategies, i.e.,

a random selection strategy (randomly choose some of DE variants in

each generation) and population-based algorithm portfolio (PAP) [12].

Experimental results show that the proposed PMSS can self-adaptively

select a best-performing DE variant among all the variants and can take

advantage of the strength of different DE variants.

The remainder of this paper is organized as follows. Sections 2 and 3

brieﬂy introduce the original DE and review previous studies on DE,

respectively. In Section 4, the proposed PMSS is presented in detail. The

results and parameter analyses are reported in Section 5. In Section 6, our

proposed strategy is employed to solve the energy consumption problem

of sea-rail intermodal transportation planning event. Finally, conclusions

are drawn in Section 7.

2. Differential evolution

Without loss of generality, we consider a single objective minimiza-

tion problem formulated as follows:





¼ min

2Ω

; x

2 S 

j¼1



; U



(1)

where f denotes the objective function, x

¼ðx

i;1

; …; x

i;D

Þ is a D-dimen-

sional decision vector, x* is the global optimum solution of the optimi-

zation problem, Ω  R

. L

and U

(j ¼ 1; 2;;D) are the lower and upper

bounds of the jth decision variable of x

, respectively, and S is the search

space.

Mutation, crossover, and selection are the three main operators in DE.

¼ðx

i;1

; x

i;2

; …; x

i;D

Þ and X

; x

; …; x

denote the i-th target

vector and the population at G-th generation, respectively.

The procedure of DE can be formulated as follows [21]:

1) Initialization: Set F, CR, NP, and maximum number of generations

max

. Initial individuals x

ð i ¼ 1; 2; …; NPÞ are generated randomly

from S. The current generation G is set to be 0.

Fig. 1. Generic framework of PMSS.

Q. Fan et al. Swarm and Evolutionary Computation 44 (2019) 1–17

2) Mutation: After initialization operation, for each target vector x

the current population, a mutation strategy is utilized to produce a

mutant vector v

. Some useful mutation operators are given as

follows:

“DE=rand=1”: v

¼ x

þ F ⋅



 x



; (2)

“DE=rand=2”: v

¼ x

þ F ⋅



 x



þ F ⋅



 x



; (3)

“DE=current  to  beat=1”: v

¼ x

þ F ⋅



best

 x



þ F ⋅



 x



;

(4)

“DE=current  to  best=2”: v

¼ x

þ F ⋅



best

 x



þ F ⋅



 x

þ x

 x



;

(5)

“DE=rand  to  best=1”: v

¼ x

þ F ⋅



best

 x



þ F ⋅



 x



;

(6)

where r

, r

, and r

are mutually exclusive integers randomly

chosen within the range [1, NP], and are also different from the index i

(i.e. r

6¼ r

6¼ i); x

best

is the target vector with the best

ﬁtness value at G-th generation.

3) Crossover: For each target vector

, a trial vector u

is generated as

follows:

(

; rand

 CR or j ¼ j

rand

; otherwise

; (7)

where rand

and j

rand

are a random number uniformly generated within

the range [0, 1] and a randomly selected integer within the range [1, D],

respectively.

4) Selection: The trial vector u

competes with its target vector x

and

then the better one will be selected for the next generation:

Gþ1



; f





 f





; otherwise

; (8)

5) Implement Steps 2 to 4 repeatedly until the number of generations is

equal to G

max

3. Related work

Although DE is one of the most competitive meta-heuristic algorithms

and has been applied to solve a variety of optimization problems in

practice, its performance is heavily dependent on parameter settings and

selected strategies. To alleviate this problem, DE researchers proposed

various techniques [22,23] to enhance the performance of DE. In the

following, a number of popular DE variants are reviewed according to the

parameter control method, strategy improvement, and use of other

methods.

3.1. Parameter control method

DE has three main control parameters, i.e., mutation control param-

eter F, crossover control parameter CR, and population size NP. These

parameters signiﬁcantly affect the performance of DE. Therefore, many

empirical guidelines of parameter setting [9,24–27] have been intro-

duced to enhance the performance of DE. However, these guidelines are

often inconsistent or even confusing, as they are based on individual

experiments [28]. To avoid handcrafting the control parameters, various

techniques have been developed to automatically determine the control

parameters F and CR. For Example, Abbass [29] utilized a normal dis-

tribution function to generate the control parameters F and CR in a

self-adaptive Pareto DE algorithm (SPDE). In Ref. [30], a DE with

self-adaptive parameter control (jDE) is proposed. In jDE, F and CR are

encoded into each individual and are generated by a uniform distribution

function. In a self-adaptive DE (SaDE) [28], F in each individual is

randomly generated from a normal distribution function, while CR of

each individual in population is self-adaptively generated by a normal

distribution function in which a mean value is updated by the previous

successful experience. Ghosh et al. [31] used the objective function value

of each individual to update the control parameters. Wang et al. [32]

introduced a DE based on covariance matrix learning and bimodal dis-

tribution parameter setting (CoBiDE), in which F and CR of each indi-

vidual are generated using bimodal distribution consisting of two Cauchy

distribution functions. In Ref. [33], a success-history based mechanism is

utilized to automatically produce F and CR in success-history based

adaptive DE (SHADE), which is a modiﬁed version of JADE. This

parameter adaptation mechanism is also used in Ref. [34]. Fan and Yan

[35] used a weighted average value to update the mean value of a normal

distribution function. Moreover, the encodings of

F and CR are at the

gene and individual levels, respectively. Recently, zoning evolution

proposed by Fan and Yan [36] is utilized to generate appropriate com-

binations of F and CR in a self-adaptive DE with zoning evolution of

control parameters and adaptive mutation strategies (ZEPDE). In addi-

tion to the above methods, constant control parameter combination

methods have also been used to enhance the performance of DE. For

example, an ensemble of mutation strategies and control parameters with

DE (EPSDE) is proposed in Ref. [16]. Similar to EPSDE, Wang et al. [37]

used three ﬁxed combinations of control parameters F and CR in a

composite DE (CoDE). Overall, adaptive and self-adaptive parameter

control methods can effectively improve the performance of DE, although

it still needs further study to evaluate their performance under different

trial vector generation strategies [38].

3.2. Strategy improvement

The optimization performance of DE is strongly inﬂuenced by the

choice of mutation and crossover strategies. For Example, it is known that

mutation strategy DE/rand/1 is suited for exploration, while mutation

strategy DE/best/1 is better for exploitation. To improve mutation and

crossover strategies, Islam et al. [39] proposed a modiﬁed DE with p-best

crossover (MDE_pBX). In MDE_pBX, novel mutation crossover strategies

are utilized to enhance the optimization performance. Wang et al. [40]

presented an orthogonal crossover operator based on orthogonal design.

In Ref. [41], a normal random variable is utilized to enhance the muta-

tion strategy. Gong et al. [42] proposed a crossover rate repair method, in

which a number of DE variants are integrated. Yu et al. [43] presented a

variant of the greedy mutation operator DE/best/1 in an adaptive DE

(ADE). Guo and Yang [44] presented an eigenvector-based crossover

operator, which can signiﬁcantly enhance the DE performance on some

non-separable unimodal functions. A multiple exponential recombina-

tion is proposed in Ref. [45], where it was shown that the proposed

crossover operator is effective compared with the binomial crossover

strategy. Cai and Wang [46] proposed a hybrid linkage crossover (HLX)

to solve the weakness of linkage-blind in DE.

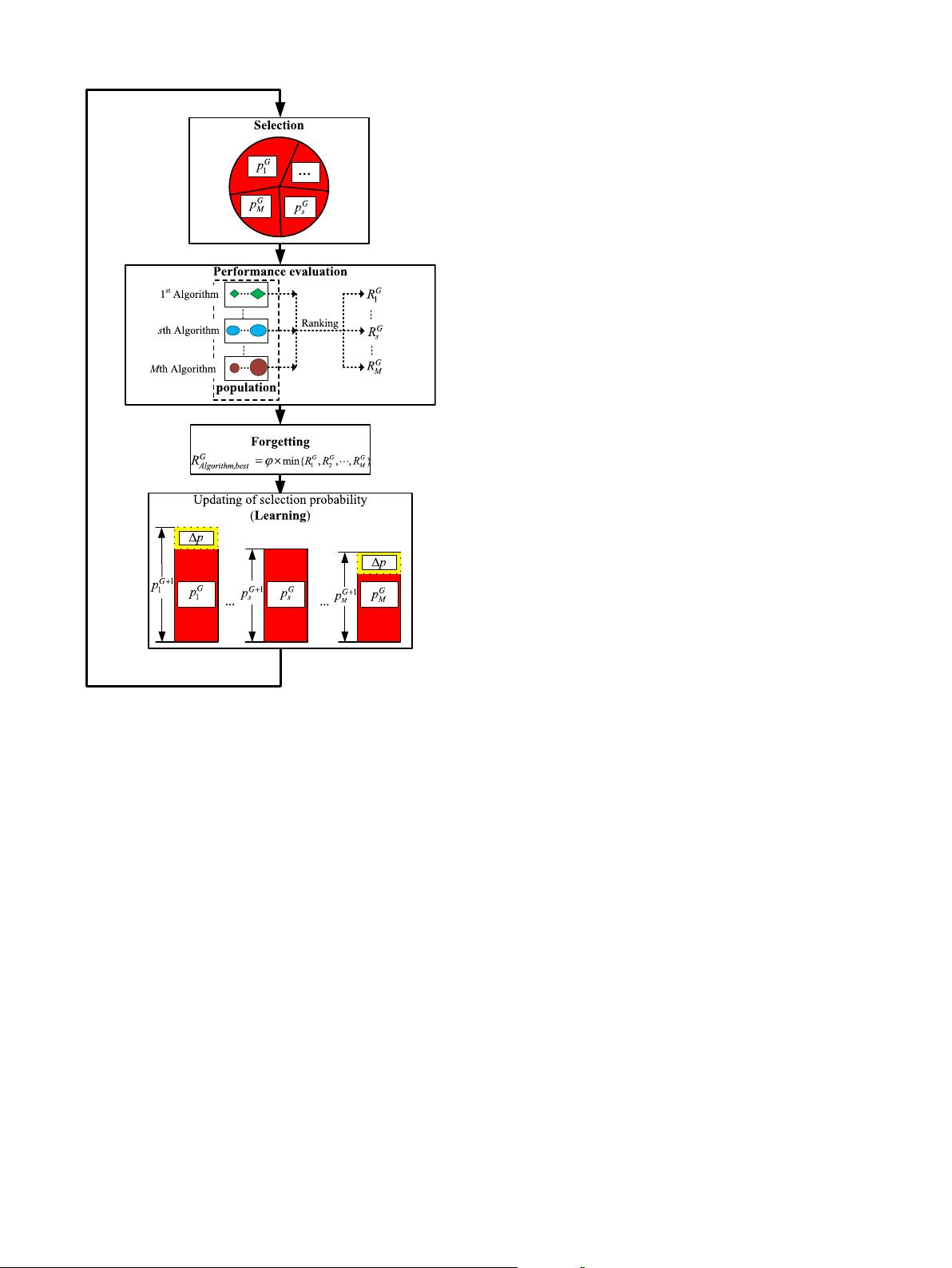
For ensemble of multiple strategies, Qin et al. [28] used a pool of

mutation strategies in SaDE, where the selection of mutation strategy is

based on the previous successful experience. Wang et al. [37] selected

three mutation strategies for enhancing the performance of DE. In

Ref. [47], a strategy adaptation mechanism (SaM) is proposed to auto-

matically choose a more suitable mutation strategy to deal with a

particular type of optimization problem. In Refs. [35,36], two different

techniques are proposed to carry out the adaptation of mutation strategy.

Q. Fan et al. Swarm and Evolutionary Computation 44 (2019) 1–17

剩余16页未读，继续阅读

评论收藏

内容反馈

weixin_38695471

粉丝: 3
资源: 911

A performance-driven multi-algorithm selection strategy for ener...

最新资源

A performance-driven multi-algorithm selection strategy for ener...

A Priori Data-driven Multi-clustered Reservoir Generation Algorithm for Echo State Network

Test-Driven Java Development(PACKT,2015)

Designing Event-Driven Systems

A Data-Driven Game Object System

JESD47G Stress-Test-Driven Qualification of Integrated Circuits

A Data-Driven Approach for Multi-level Packing Problems

Test-Driven Development: A Practical Guide

Thoughtful Machine Learning with Python A Test-Driven Approach 无水印pdf 0分

Test-Driven Java Development

A skin membrane-driven membrane algorithm for many-objective optimization

Lessons Learned in Software Testing A Context-Driven Approach

Practical Test-Driven Development using C# 7.epub

Test-Driven Java Development - Second Edition.pdf

Knowledge-driven Encode, Retrieve, Paraphrase for MedicalImageReport.pdf

Energy optimization of a battery-powered device.pdf

Thoughtful Machine Learning with Python: A Test-Driven Approach

基于CORDIC的反正弦和反余弦计算的FPGA实现

BA无标度网络中的SIR模型

使用3DCNN和卷积LSTM进行手势识别学习时空特征

基于三次贝塞尔曲线的类汽车曲率连续路径平滑

基于机器学习的设备剩余寿命预测方法综述

基于维纳过程的退化模型，具有递归过滤算法，可用于估计剩余使用寿命

基于FPGA的奇异值和特征值分解的快速实现。

磁悬浮系统自适应模糊PID控制器的设计

最新资源