Bc介子轻子衰变的两环QCD校正资源-CSDN文库

Open

Access

79 浏览量 2020-04-04 12:49:39 上传评论收藏 281KB PDF 举报

资源推荐

资源详情

资源评论

Physics Letters B 748 (2015) 443–450

Contents lists available at ScienceDirect

Physics Letters B

www.elsevier.com/locate/physletb

Two-loop QCD corrections to B

meson leptonic decays

Long-Bin Chen

, Cong-Feng Qiao

a,b,∗

School of Physics, University of Chinese Academy of Sciences, YuQuan Road 19A, Beijing 100049, China

CAS Center for Excellence in Particle Physics, Beijing 100049, China

a r t i c l e i n f o a b s t r a c t

Article history:

Received

22 March 2015

Received

in revised form 9 July 2015

Accepted

18 July 2015

Available

online 22 July 2015

Editor:

B. Grinstein

The two-loop quantum chromodynamics (QCD) radiative corrections to the B

meson leptonic decay rate

are calculated in the framework of the non-relativistic QCD (NRQCD) factorization formalism. Two types

of master integrals appearing in the calculation are obtained analytically for the ﬁrst time. We calculate

the short-distance coeﬃcient of the leading matrix element to order α

by matching the full perturbative

QCD calculation results to the corresponding NRQCD results. The result presented in this work helps the

evaluation of both the B

leptonic decay constant and the Cabibbo–Kobayashi–Maskawa (CKM) matrix

element |V

| to the full next-to-next-to-leading-order (NNLO) degree of accuracy.

(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP

The advent of the non-relativistic quantum chromodynamics (NRQCD) factorization formalism has improved the reliability of investiga-

tions

on heavy quarkonium [1], thereby also improving the understanding of the strong interaction. It has been noted that for quarkonium

production and decays, in many cases, the leading-order calculation in the framework of NRQCD is inadequate. However, the discrepancies

between the leading-order calculations and the experimental results can be mostly rectiﬁed by including higher-order corrections, which

has stimulated various investigations in this respect.

The

meson system, which contains two different ﬂavors of heavy quarks, possesses some peculiar characteristics different from those

of heavy quarkonium and has recently attracted considerable interest, especially with the progress of the LHCb experiment [2]. Although

the B

meson is highly elusive in experiments, the information obtained from investigations thereof is extremely valuable, including

insights into certain aspects of quantum chromodynamics (QCD), the weak interaction and even new physics. In the

bc system, the higher

excited states will predominantly cascade down into the ground state, the pseudoscalar B

meson, through hadronic or electromagnetic

transitions, and this state will then decay into lighter hadrons or leptons via the weak interaction.

Using

the NRQCD formalism, the B

meson decay amplitude can be expressed in terms of perturbative QCD (pQCD)-calculable short-

distance

coeﬃcients multiplied by non-pertubative NRQCD matrix elements. The expression for the leading-order (LO) B

meson leptonic

decay width is simple and has long been known, and the next-to-leading-order calculation was completed by Braaten and Fleming two

decades ago [3]. In this work, we compute in pQCD the two-loop radiative corrections to the pseudoscalar B

meson leptonic decay rate,

i.e., the short-distance coeﬃcient for the leading matrix element at next-to-next-to-leading-order (NNLO), by matching the perturbative

result in full QCD with the corresponding perturbative calculation in NRQCD.

The

calculation of massive two-loop Feynman integrals is rather diﬃcult, especially with two mass scales. For this reason, only a few

master integrals with different massive propagators have been successfully calculated [4–6]. The method of differential equations proves

to be an eﬃcient and powerful technique for the calculation of Feynman integrals. Recently, it was shown by Henn that the solution of

differential equations will be considerably simpliﬁed if the bases of the master integrals are properly chosen [7]. In our calculation, by

employing the technique of differential equations and choosing certain bases for the master integrals, we successfully obtain the master

integrals required in the calculation of the two-loop QCD corrections to the B

meson leptonic decays.

The

meson leptonic decays, namely, B

→ lν

, where l is e, μ, or τ , are heavy-quark-annihilation processes through an axial-vector

current, which are very important to the study of B

physics, although they have not yet been (but are expected to be) measured.

Corresponding author at: School of Physics, University of Chinese Academy of Sciences, YuQuan Road 19A, Beijing 100049, China.

E-mail

addresses: chenglogbin10@mails.ucas.ac.cn (L.-B. Chen), qiaocf@ucas.ac.cn (C.-F. Qiao).

http://dx.doi.org/10.1016/j.physletb.2015.07.043

0370-2693/

SCOAP

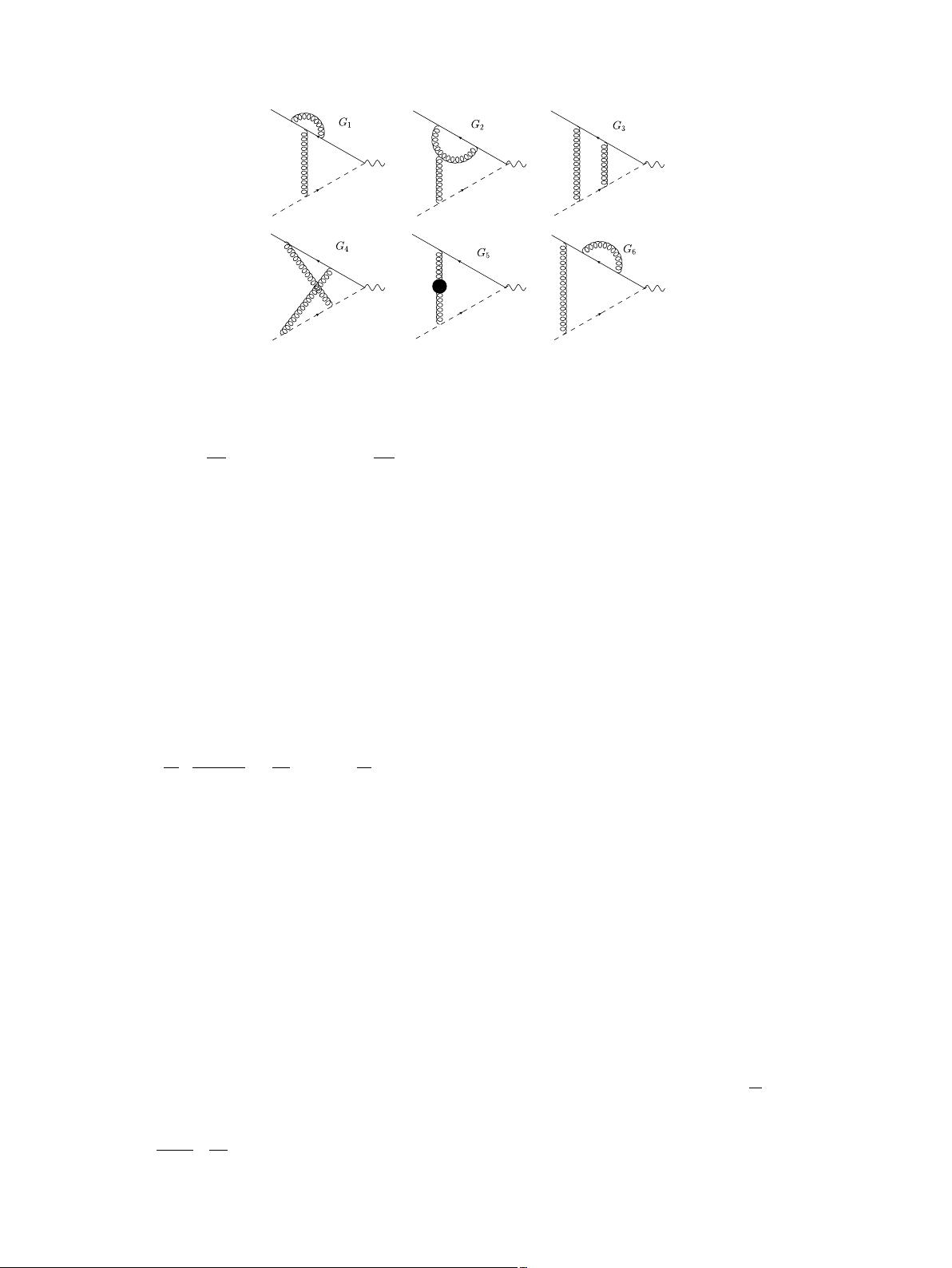
444 L.-B. Chen, C.-F. Qiao / Physics Letters B 748 (2015) 443–450

Fig. 1. Two-loop diagrams that contribute to the processes of interest. For G

1,2,6

, the symmetric diagrams are implied. The diagram G

contains contributions from massless

fermions, gluons, ghosts, and the massive fermions.

Theoretically, the decay rates can be formulated as follows:

(B

→ 



) =

8π





1 −





, (1)

where V

denotes the Cabibbo–Kobayashi–Maskawa (CKM) matrix element; M and m



represent the masses of the B

meson and the

charged leptons, respectively; and G

is the Fermi coupling constant of the weak interaction. Generally, the B

decay constant f

deﬁned in terms of the transition matrix element of the charged weak current as follows:

0|

bγ

c|B

(p)=if

, (2)

which parameterizes the effects of the strong interaction and contains both perturbative and non-perturbative contributions.

The

short-distance contribution can be isolated and calculated in perturbation theory by matching the charged weak current in QCD

to a series of operators in NRQCD. In the rest frame of the B

system, up to corrections of order v

(where v is the relative velocity of

heavy quarks within the meson), the matching relation reads [3]

0|

bγ

c|B

(p)=C

0|χ

†

(p)+C

0|(Dχ

)

†

· Dψ

(p)+... , (3)

where C

and C

are short-distance coeﬃcients that depend on the heavy quark masses, the renormalization scale μ, and the strong

coupling α

. The coeﬃcients C

and C

are determined by matching the perturbative calculation of the matrix elements in full QCD with

the results obtained in the framework of NRQCD [3]. The coeﬃcient C

was obtained at one-loop-order in Ref. [3], i.e.,

= 1 +



− m

+ m

log

− 2



+ (

)

, m

, μ). (4)

In this work, we analytically calculate the NNLO QCD corrections to the short-distance coeﬃcient of the leading-order matrix element in

the v

expansion, i.e., co

, which will allow the theoretical predictions for the B

leptonic decay rates to be improved to NNLO accuracy.

calculating the two-loop contributions in full QCD, we ﬁrst revisit the one-loop QCD corrections to the B

meson leptonic decays. At

one-loop order, there is only one diagram in the Feynman gauge, and the Mathematica package FeynArts [8] is employed to generate the

amplitude. FeynCalc [9] is used in combination with code written by ourselves to manipulate the γ -matrix algebra and spin projections,

and FIRE [10] is used in combination with $Apart [11] to reduce all related integrals to a set of master integrals. In the one-loop case,

the integrals are merely subject to two massive tadpoles. After performing the standard renormalization procedure, we then obtain the

coeﬃcient C

at the order of α

, which agrees with Ref. [3].

The

topologically independent two-loop-order Feynman diagrams are schematically shown in Fig. 1, where the solid line represents

the bottom quark and the dashed line represents the charm quark. Note that in this ﬁgure, the diagrams of G

1,2,6

in which the solid and

dashed lines are exchanged are implied. Although the W

boson may couple to the charm and bottom quarks through both vector and

axial-vector currents, in practice, only the axial-vector current contributes to the annihilation decays of the pseudoscalar B

meson. The

calculation of the two-loop amplitude requires the same procedure used in the one-loop case. The most diﬃcult part of the two-loop

calculation in this work resides in the evaluation of the master integrals, as explained in the following.

The master integrals with which we are confronted in the calculation are shown in Fig. 2, where the dotted, dashed, and solid lines

correspond to the gluon, charm quark and bottom quark propagators, respectively; the incoming and outgoing wavy lines in diagrams

and I

have a ﬁctitious invariant mass of p

= (m

+ m

)

. To obtain the master integrals by employing the technique of differential

equations and for the sake of compactness, we encapsulate the two heavy quark masses in a new parameter, x =

, and normalize the

loop integrals in terms of



[

q]=



iπ

D/2





−

2



q , (5)

where γ

is the Euler constant and μ is the renormalization scale.

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38694541

粉丝: 12
资源: 926

Bc介子轻子衰变的两环QCD校正

改进的Bc介子衰变的扰动QCD形式主义

对大型强子对撞机具有轻子衰变的WZZ产物进行NLO QCD + NLO EW校正

扰动QCD方法中Bc介子的半轻子衰变为S波charm态

通过W +玻色子衰变对Bc和Bc *产生的次优QCD校正

大型强子对撞机的轻子衰变导致三阶W产生的下一阶QCD和电弱校正

四味晶格QCD的B和D介子轻子衰变常数

三体非轻子B衰变和QCD分解

Bs介子的半轻子衰变中的DsJ（2860）

包括软光子区域的B-和D-介子的辐射轻子衰变的因式分解

强重介子的衰变常数中的强等位旋打破的局部对偶QCD和规则

辐射轻子B衰变的因式分解和色散关系

QCD和规则分析重轻介子的质量和衰变常数

稀有衰变Bs，d→μ+ μ−的增强电磁校正

轻张量介子的半轻子衰变

QCD中$ \ chi _ {c1}（1p）$介子的稀有半轻子衰变

轻度Ds在两味晶格QCD中衰变

研究Majorana中微子对B-介子半轻子稀有衰变的贡献

论文研究 - 无论如何，Muon是介子：介子还是轻子！

网络技术-网络基础-用重味夸克半轻子衰变电子和带电强省略和粲夸克半轻子衰变电子的相对产额.pdf

双重子的弱衰变：对π介子系统的衰变

| Vcb | 半轻子衰变B→Dℓν¯ℓ和D介子分布振幅的特性

QCD和规则的重轻介子的径向激发

重正化组演化对（半）轻子介子衰变的新物理学贡献

用扰动QCD方法分析B c→J /ψa 1（1260）+

通过顶夸克的显性半轻子衰变间接搜索轻的希格斯玻色子→（→/ +）+（→）

在标准模型和通用超维模型中，半轻子B→S衰变

涉及轴矢量介子的底介子Δ= 1衰变的研究

最新资源