没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
Radial basis function (RBF) based-identification proportional–integral–derivative (PID) can automatically adjust the parameters of PID controller.with strong self-organization, self-learning and self-adaptive ability.However, the compound controller has complex weight updating algorithm and.large calculation. Memristor, applied well to the investigation of storage circuit and artificial intelligence, is a nonlinear element with memory function. Thus, it can be introduced to RBF neural network as
资源推荐
资源详情
资源评论

© Springer International Publishing Switzerland 2014
Z. Zeng et al. (Eds.): ISNN 2014, LNCS 8866, pp. 150–158, 2014.
DOI: 10.1007/978-3-319-12436-0_17
Memristive Radial Basis Function Neural Network
for Parameters Adjustment of PID Controller
Xiaojuan Li
1
, Shukai Duan
1(
)
, Lidan Wang
1
, Tingwen Huang
2
, and Yiran Chen
3
1
College of Electronic and Information Engineering,
Southwest University, Chongqing, China
duansk@swu.edu.cn
2
Department of Electrical and Computer Engineering,
Texas A&M University, Doha, Qatar
3
Department of Electrical and Computer Engineering,
University of Pittsburgh, Pittsburgh, USA
Abstract. Radial basis function (RBF) based-identification proportional–
integral–derivative (PID) can automatically adjust the parameters of PID con-
troller with strong self-organization, self-learning and self-adaptive ability.
However, the compound controller has complex weight updating algorithm and
large calculation. Memristor, applied well to the investigation of storage circuit
and artificial intelligence, is a nonlinear element with memory function. Thus, it
can be introduced to RBF neural network as electronic synapse to save and up-
date the synaptic weights. This paper builds a model of memristive RBF-PID
(MRBF-PID), and proposes the updating algorithm of weight upon
memristance. The proposed MRBF-PID is used for the control of a nonlinear
system. Its controlling effect is showed by numerical simulation experiment.
Keywords: Memristor · Radial basis function neural network · PID controller ·
Simulink model
1 Introduction
Based on the completeness of circuit, Chua proposed theoretically the notion of
memristor in 1971 [1]. In 2008, a team at HP Labs announced that the physical model
of memristor had been realized, which verified the existence of memristor [2-3], and
attracted major research fields’ attention. By reason of memristor’s non-volatile
memristive behavior and dynamic change resistance characteristic, we can primely
introduce it into, for example, storage circuit, neural network and pattern recognition
etc. Memristor has nanoscale size, which can greatly simplify the circuit by being
applied in the large scale integrated circuit.
PID controller is the primary means of control in industrial control systems. In
traditional PID controller, once the parameters are identified in the process, they can
not be adjusted any more; therefore, systems can not achieve perfect controlling
effect. Radial basis function neural network (RBF) is a local approximation network.
Memristive Radial Basis Function Neural Network for Parameters Adjustment 151
It has many excellent properties, such as fast convergence, strong generalization abil-
ity and simple structure. It can approximate continuous functions with arbitrary preci-
sion. RBF-PID is a combination of radial basis function neural network and the
traditional PID controller. It boasts not only the ability to dynamically control the
parameters of PID system, but also the ability to optimize the system parameters and
improve the controlling effect through neural networks’ self-learning ability.
This paper is organized as follows. Section 2 gives a brief overview on the PID
controller based on RBF network
. Section 3 introduces HP Memristor Model.
Memristive RBF-PID Model is proposed in Section 4. Numerical simulation re-
sults are presented in Section 5. Finally, Section 6 concludes the work.
2 PID Controller Based on RBF Network
2.1 RBF Network
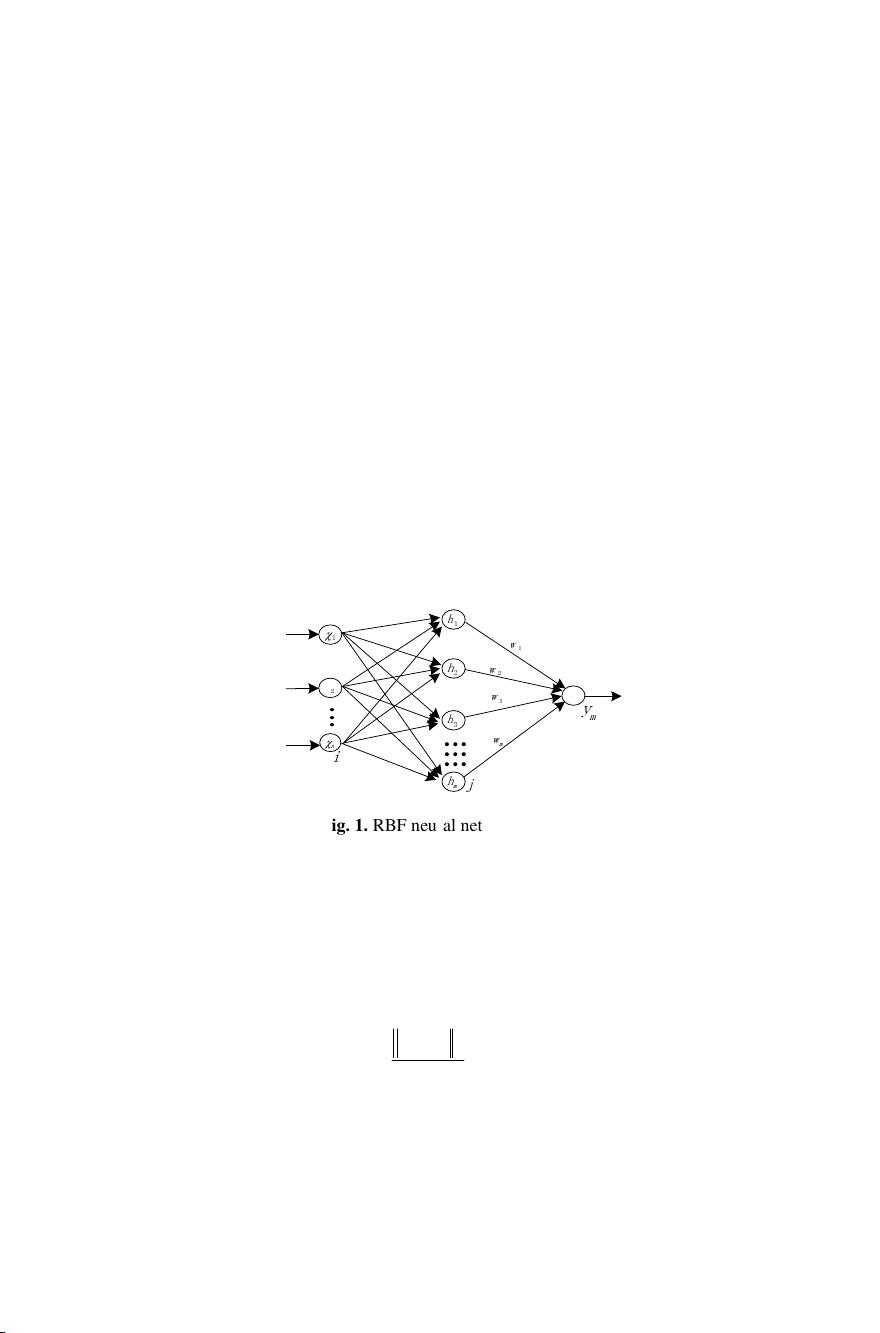
RBF network was proposed in 1988 [5], which possessed good generalization ability
and simple network structure. We supposed that RBF network was provided with n
input nodes, M hidden layer nodes and one output node. The structure is shown in
Fig. 1.
1
χ
2
χ
n
χ
2
h
3
h
m
h
1
w
2
w
3
w
m
w
m
y
i
j
1
h
Fig. 1. RBF neural network structure
Generally we select the appropriate hidden layer activation function (Radial Basis
Function, namely RBF) in accordance with the need. Gaussian function is used in this
paper.
By the structure of RBF network, the input vector of the first layer is X=[x
1
, x
2
,…,
x
n
]
T
. The output vector of hidden layer, namely Radial basis vector, is H=[h
1
,h
2
,…,
h
m
]
T
, where h
j
is Gaussian function:
2
2
exp( ),( 1, 2,..., )
2
j
j
j
xC
hjm
b
−
=− = (1)
In above equation, m represents the number of the hidden layer neuron.
C
j
=[c
j1
,c
j2
,…,c
ji
,…,c
jn
]
T
,(i=1,2,…,n) denotes the center vector of jth neuron. b
j
denotes
the basis width of jth neuron’s RBF, which determines the width of basis function
剩余8页未读,继续阅读
资源评论

weixin_38694023
- 粉丝: 4
- 资源: 976
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功