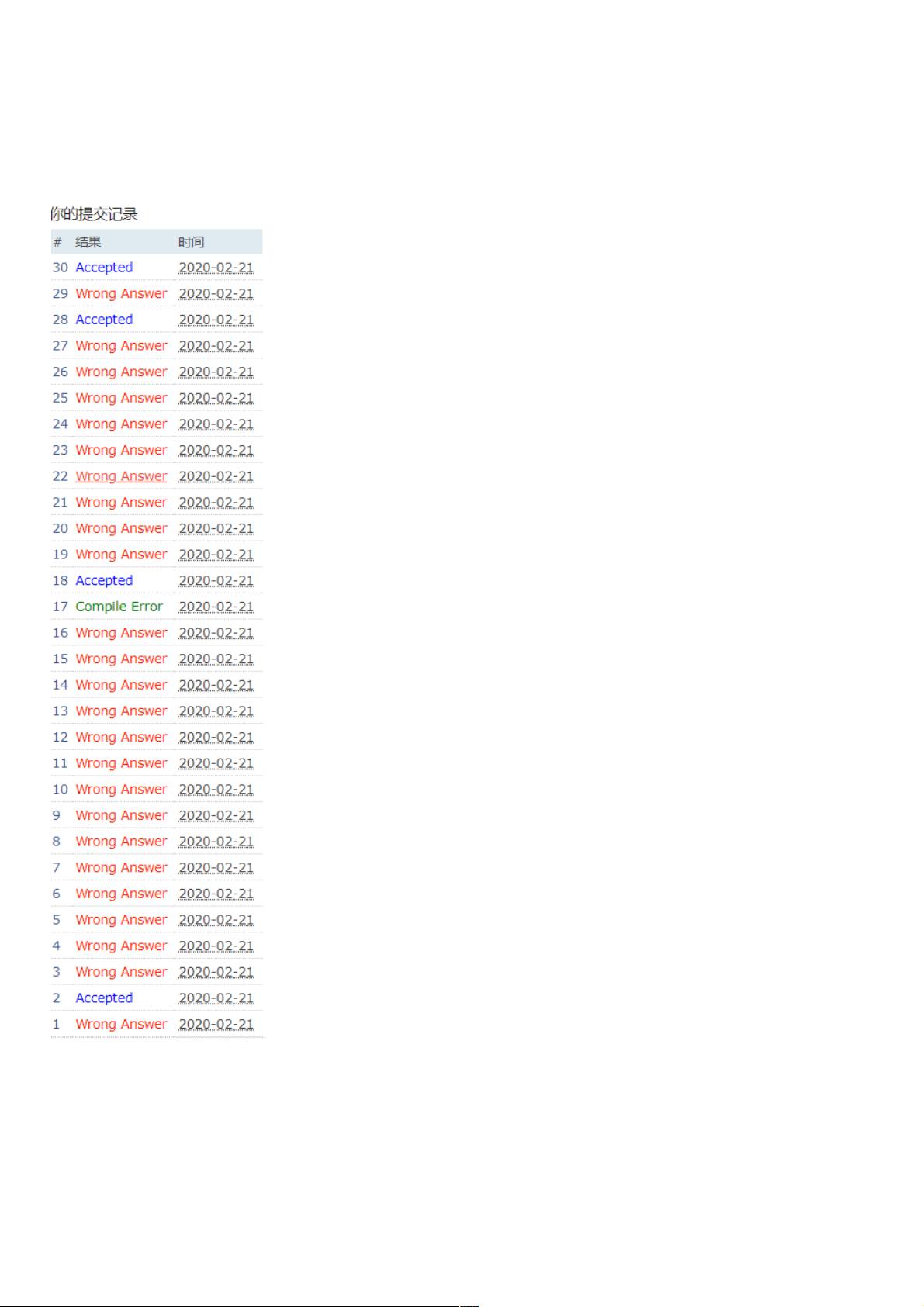
1258:Agri-Net（弗洛伊德）

1258:Agri-Net 弗洛伊德思路： 先找到与1相连最短的那条路，然后再更新与1和刚才相连的点每个与其他点最短的路存储，然后再找到下一个点，再找到这三个点与其他点最短路存储，以此类推。 Prim代码： 除了最后一个ac代码是自己的其他的都不是，wa的全是自己进步的过程，加油！ #include #include #include #include #include #include #include #include #include #include #include #include #include #include #include #include #define ll 中的“1258:Agri-Net（弗洛伊德）”指的是一道编程竞赛题目，该题目可能要求解决图论中的最短路径问题，使用了弗洛伊德算法作为解决方案。 中提到的“弗洛伊德思路”是指弗洛伊德算法的基本思想。弗洛伊德算法是一种解决所有顶点对之间最短路径的动态规划方法。它通过逐步增加中间节点来更新最短路径，从一个点开始，找到与它相连的最短边，然后更新这个点和新连接点与其他点的最短路径，接着选择下一个点，重复此过程，直到所有点都被包含在内。 Prim代码部分展示了Prim算法的实现。Prim算法是求解加权无向图中最小生成树的一种方法，它从一个顶点开始，每次添加一条与当前树中顶点相连且权重最小的边，直至包含所有顶点。这里的代码用C++编写，通过维护一个标记数组`mm`表示哪些顶点已被加入最小生成树，同时使用`len`矩阵存储边的长度，`dis`数组记录每个顶点到已构造树的最短距离，最后返回最小生成树的总权重。 `Kruskal代码`部分则是Kruskal算法的实现。Kruskal算法同样用于寻找最小生成树，但它的策略是按边的权重从小到大进行选择，只有当所选边不构成环时才将其加入树中。这里使用并查集数据结构来判断新加入的边是否会形成环，通过`GetValue`函数查找每个元素的根节点，如果两个端点的根节点不同，则这条边可以安全添加。 标签中的“include”可能表示这些代码包含了多个头文件，这些头文件提供了必要的库函数，如输入/输出操作、数据类型定义等。 部分内容中，可以看到Prim和Kruskal两种算法的实现细节，以及它们如何处理图的边和顶点。在Prim算法中，通过不断找到与已连接部分具有最小边权的顶点来扩展最小生成树。而在Kruskal算法中，通过排序边的权重并检查并查集避免环路，逐渐构建最小生成树。 这段内容涵盖了图论中的最短路径算法（弗洛伊德算法）和最小生成树算法（Prim和Kruskal算法），并提供了这两种算法的C++实现。这些算法是图论中的核心概念，常用于解决实际问题，如网络优化、交通规划等。在编程竞赛或实际开发中，理解和熟练运用这些算法对于解决涉及图的问题至关重要。