Grover算法是由Lov Grover于1996年提出的,用于在无序数据库中进行量子搜索的算法。该算法基于量子叠加态和量子干涉原理,其搜索速度比经典算法快得多。Grover算法的重要性在于,它证明了量子计算机对于某些基于问题的算法相较于经典计算机具有明显的加速潜力。对于一个无序数据库的问题,一个经典计算机平均需要2N次查询才能找到目标项,而Grover算法只需要次,这在N非常大时具有显著的效率优势。 然而,Grover算法在某些情况下存在局限性。当标记项(即我们要查找的特定元素)的比例超过数据库中总数的四分之一时,成功概率会迅速下降。为了解决这个问题,Panchi Li和Kaoping Song两位学者提出了自适应相位匹配的方法。自适应相位匹配是一种改进技术,用于提高当标记项比例增加时Grover算法的成功概率。通过应用这种新的相位匹配技术,当标记项的比例增加到一定程度时,可以在最多两次Grover迭代后达到成功概率等于1,即找到目标项。 研究论文中提到的自适应相位匹配策略的验证是通过一个搜索示例进行的。论文提到的关键词包括量子计算、量子搜索、Grover算法、相位匹配以及自适应相位匹配。这些关键词涉及的研究领域不仅限于量子算法,还包括量子计算的基本原理和量子信息科学的其他方面。 Shor的素数分解算法和Grover的量子搜索算法被认为是两项伟大的量子算法。Shor算法可以高效地解决大整数分解问题,是量子计算机能够显著加速解决的另一个著名问题。与Grover算法类似,Shor算法也依赖于量子计算机特有的并行处理和量子态的叠加性质来实现指数级的速度提升。 在量子搜索的背景下,自适应相位匹配概念的提出,是为了解决Grover算法在搜索效率上的一个瓶颈。传统上,随着数据库中标记项数量的增加,Grover算法的成功概率会降低,这在搜索效率上是不利的。Panchi Li和Kaoping Song提出的自适应相位匹配技术,通过动态调整算法中的相位因子来适应数据库中标记项比例的变化,从而在标记项比例较高时仍能保持较高的搜索成功概率。 这种自适应方法的重要性在于,它为Grover算法的工程实现提供了一种新的思路,尤其是在处理复杂数据库时,能够更加灵活地调整算法以适应不同的搜索场景。虽然论文内容并不详细说明自适应相位匹配的具体实现机制,但从其描述可以推断,该技术涉及对量子态进行更加精细的操作,这包括了量子逻辑门的应用以及量子位相的精确控制。这说明了量子算法的实现并不是简单的,它需要针对算法特点,设计精细的量子操作过程。 此外,论文提到的自适应相位匹配技术还显示出量子计算领域的一个研究趋势,即如何在量子算法中更有效地利用量子态的相位信息来提升算法性能。量子相位是量子态的一个基本特征,它对量子干涉和量子纠缠等现象起着核心作用。理解并控制量子相位可以帮助我们设计出更为高效和精确的量子算法,这对于量子计算技术的进一步发展至关重要。 通过上述讨论,可以看出Grover算法中的自适应相位匹配技术是量子信息科学领域中一个重要的研究方向。它不仅为解决Grover算法的效率问题提供了可能的解决方案,而且反映了量子计算领域在理论和实践层面的深度研究和不断探索。未来,随着对该技术研究的深入,我们有望看到更多的量子算法得到改进,以及量子计算机在解决复杂问题上的能力得到进一步加强。

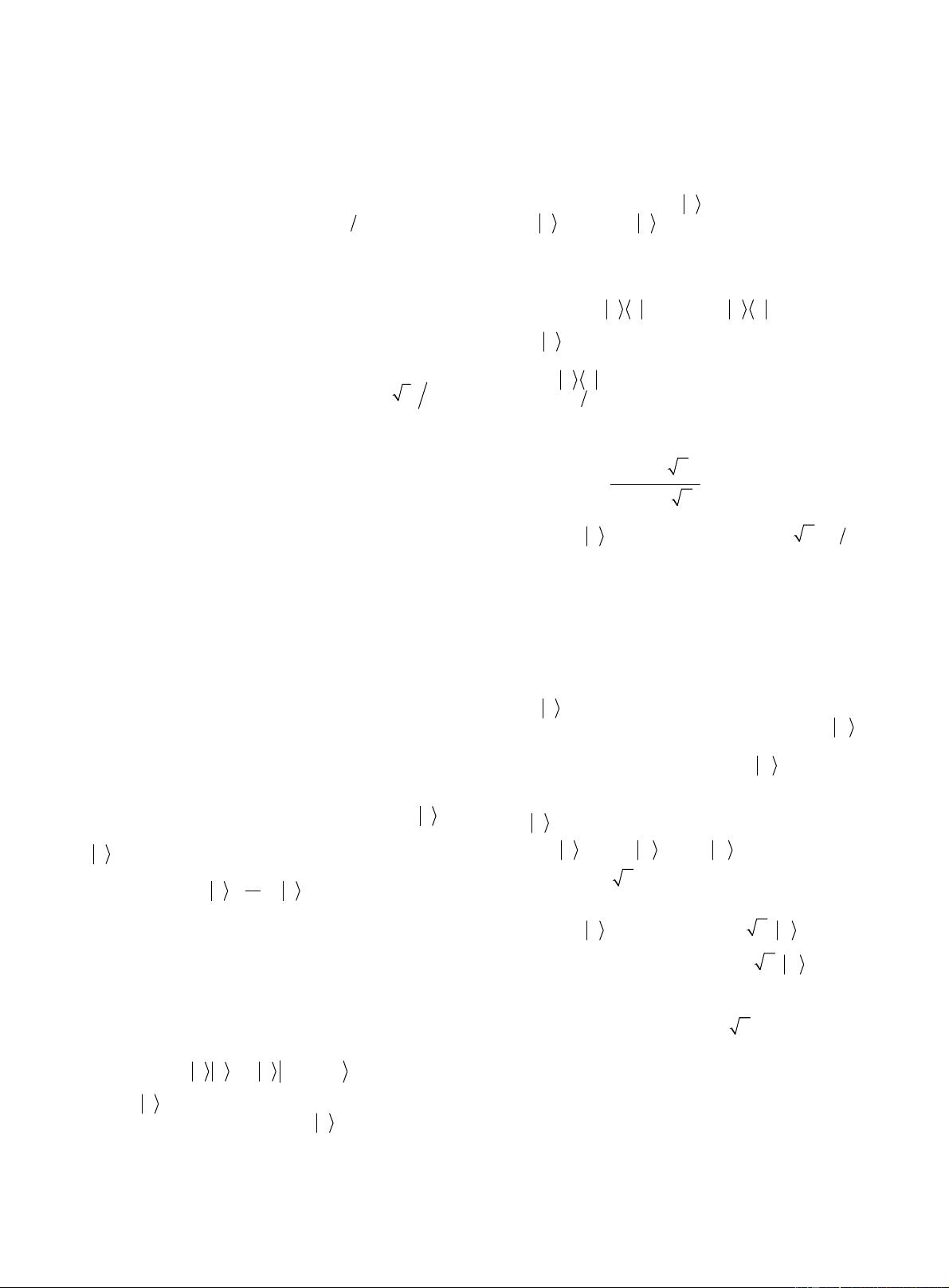
剩余6页未读,继续阅读

- 粉丝: 8
- 资源: 920
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- dataCollection-资源文件
- Java-Interview-Advanced-啊哦111
- Pear Admin Layui-资源文件
- 1615-1.6米写真机(数码印花机) sw14可编辑全套技术资料100%好用.zip
- FDG-A1∕D-56电子防盗保险柜sw16可编辑全套技术资料100%好用.zip
- A17038产品自动锁螺丝机sw17可编辑全套技术资料100%好用.zip
- 半自动U型上止焊接机(sw16可编辑+工程图)全套技术资料100%好用.zip
- 四工位高速塞棉机sw18全套技术资料100%好用.zip
- 消磁生产线sw17可编辑全套技术资料100%好用.zip
- 2.5mm铜箔焊线机sw19可编辑全套技术资料100%好用.zip
- 20T双级级水处理设备step全套技术资料100%好用.zip
- C语言编程实现不同类型的圣诞树
- HTML与JavaScript实现圣诞节飘雪效果代码详解
- 20米双层倍速链sw18可编辑全套技术资料100%好用.zip
- MC-160袋式除尘器sw18可编辑全套技术资料100%好用.zip
- 毕业设计-基于Flask健身论坛 详细文档+全部资料+高分项目.zip


 信息提交成功
信息提交成功