晶格Schwinger模型中的助焊剂展开资源-CSDN文库

Open

Access

151 浏览量 2020-04-16 06:30:47 上传评论收藏 1.09MB PDF 举报

资源推荐

资源详情

资源评论

Flux unwinding in the lattice Schwinger model

Chris Nagele,

1,2

J. Eduardo Cejudo,

Tim Byrnes,

1,3,4,5,6

and Matthew Kleban

2,6

New York University Shanghai, 1555 Century Avenue, Pudong, Shanghai 200122, China

Center for Cosmology and Particle Physics, New York University, New York, 10003, USA

State Key Laboratory of Precision Spectroscopy, School of Physical and Material Sciences,

East China Normal University, Shanghai 200062, China

NYU-ECNU Institute of Physics at NYU Shanghai, 3663 Zhongshan Road North,

Shanghai 200062, China

National Institute of Informatics, 2-1-2 Hitotsubas hi, Chiyoda-ku, Tokyo 101-8430, Japan

Department of Physics, New York University, New York, New York 10003, USA

(Received 11 January 2019; published 22 May 2019)

We study the dynamics of the massive Schwinger model on a lattice using exact diagonalization. When

periodic boundary conditions are imposed, analytic arguments indicate that a nonzero electric flux in the

initial state can “unwind” and decrease to a minimum value equal to minus its initial value, due to the

effects of a pair of charges that repeatedly traverse the spatial circle. Our numerical results support

the existence of this flux unwinding phenomenon, both for initial states containing a charged pair inserted

by han d, and when the charges are produced by Schwinger pair production. We also study boundary

conditions where charges are confined to an interval and flux unwinding cannot occur, and the massless

limit, where our resu lts agree with the predictions of the bosonized description of the Schwinger model.

DOI: 10.1103/PhysRevD.99.094501

I. INTRODUCTION

The massive Schwinger model [1]—quantum electro-

dynamics in one space and one time dimension—is a

fascinating quantum field theory that has been studied

intensively since the 1950s. It has a wide set of applica-

tions: as a simple example of a quantum gauge theory, as an

Abelian theory that nevertheless exhibits a linearly growing

potential between charges and hence a kind of confinement,

as a theory that exhibits a prototype strong/weak duality via

bosonization, and even to models of cosmic inflation in

string theory [2–4].

Most work on the Schwinger model has focused on its

static properties, such as its spectrum of excitations, the

value of the chiral condensate, etc. There has been

relatively little work, either analytical or numerical, on

time-dependent phenomena in the Schwinger model. Two

recent works include Hebenstreit et al., who considered the

dynamics of string breaking in the massive Schwinger

model using a numerical technique where the gauge field is

treated classically/statistically [5], and Buyens et al. who

studied real-time evolution of the wave function using the

matrix product states formalism in the thermodynamic

limit [6].

Despite the absence of electromagnetic waves in one

spatial dimension, the electric field in the Schwinger model

is generally time-dependent because charged particles

move and affect its value. These particles can be sponta-

neously produced by Schwinger pair production in the

quantum theory [7], or simply be present in the initial state.

In Ref. [8], a new time-dependent phenomenon was

discovered in the Schwinger model (and a broad class of

other theories) with spatially periodic boundary conditions.

A solution to the classical theory with no charges is a

homogeneous, time-independent electric field that winds

around the spatial circle. If a pair of equal and opposite

charges is present, the field accelerates the charges in

opposite directions until they collide at some point on the

opposite side of the circle (see Fig. 1). If the charges

transmit through each other, they will continue in the same

direction, unwinding two units of charge on each circuit

(charge and field strength have the same units in one

dimension). As a result, the initial value of the field will

steadily decrease. In the absence of any other dynamics, the

momentum of the charges causes the electric field to

overshoot zero, decreasing to a value with equal magnitude

and opposite sign as the initial field. This is sharply in

contrast with the case of the infinite line or boundary

conditions on an interval that forbid charges from crossing,

where a single charged pair can at most reduce the field by

two units.

Published by the American Physical Society under the terms of

the Creative Commons Attri bution 4.0 International license.

Further distribution of this work must maintain attribution to

the author(s) and the published article’s title, journal citation,

and DOI. Funded by SCO AP

PHYSICAL REVIEW D 99, 094501 (2019)

2470-0010=2019=99(9)=094501(9) 094501-1 Published by the American Physical Society

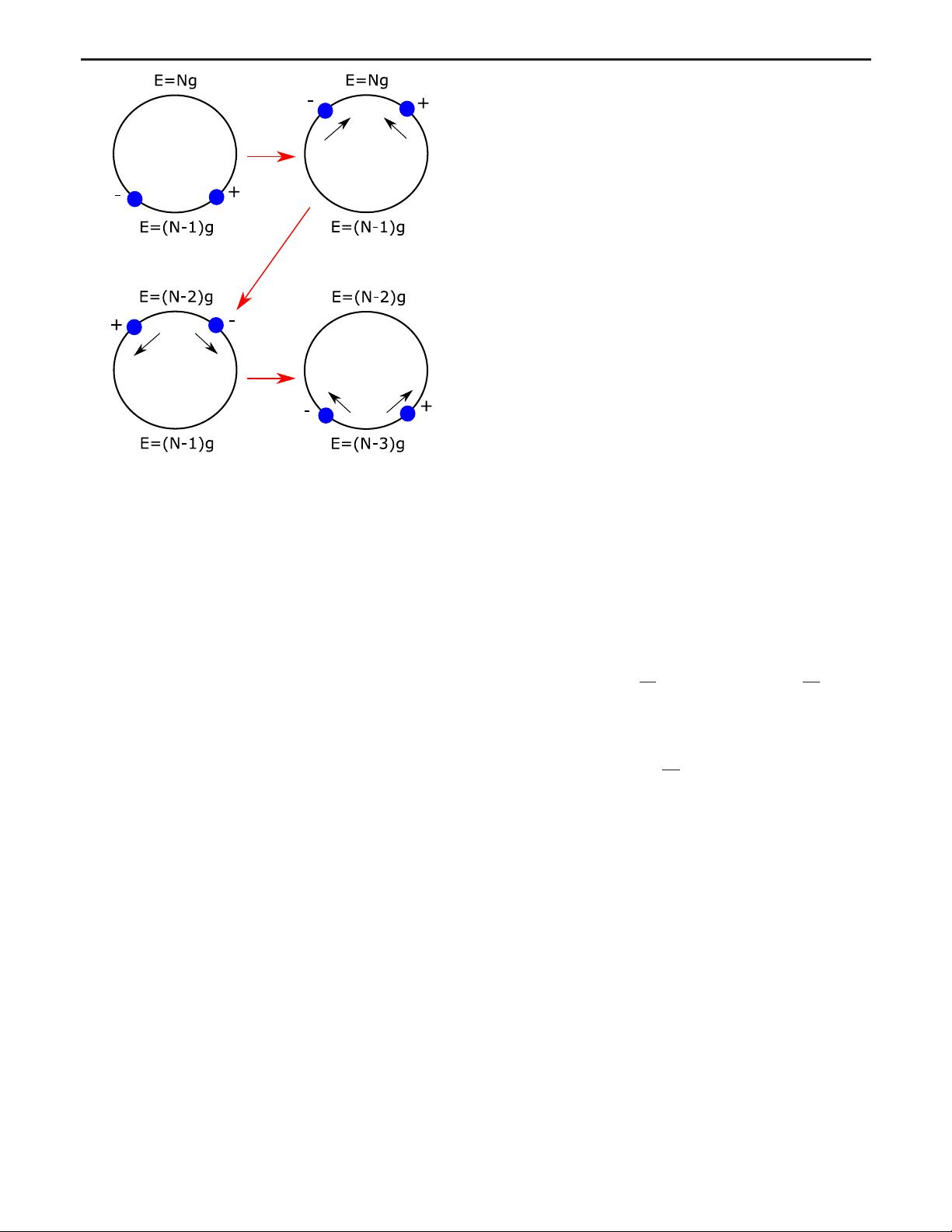
This mechanism is known as a flux discharge cascade or

flux unwinding [8], and is related to the phenomenon of

“axion monodromy” [9,10]. Note that the unwinding

mechanism depends crucially on the ability of an electron

and positron to transmit directly through each other without

reflecting, annihilating, or forming a bound state. If any of

these other processes occur with non-negligible probability,

unwinding may still happen some of the time or in one

branch of the wavefunction, but it will not necessarily be

the dominant process.

Generalizations of this unwinding process are potentially

of interest to the theory of cosmic inflation [4,11].In

theories such as string theory and supergravity with higher-

dimensional charged objects (branes) and the higher-form

analogs of electromagnetic fields they couple to, the

gravitational effect of the energy in the field can drive

exponential or quasiexponential expansion of space.

During the unwinding process the energy gradually

decreases, so that the rate of this slow-roll inflationary

expansion reduces gradually and then comes to an end.

Furthermore the initial state prior to (the analog of)

Schwinger pair production rapidly inflates and produces

an exponentially large volume, and therefore arguably

constitutes a natural initial condition for the universe.

In this paper, we examine the lattice version of the

Schwinger model and study several time-dependent phe-

nomena in a variety of parameter regimes and for several

different initial states. Most prior numerical work on the

lattice Schwinger model was restricted to what is referred to

in the literature as “open boundary conditions” (OBC),

where the electric field is fixed at the edges and charges

reflect off the boundaries [12–14]. With periodic boundary

conditions (PBC) the theory has an extra quantum

mechanical degree of freedom (d.o.f.), which can be

thought of as the electric field at one lattice site [15].

For a fixed number of lattice sites we exactly diagonalize

the full Hamiltonian, and establish that flux unwinding

indeed occurs in the nonperturbative lattice theory with

PBC when a massive charged pair is inserted in the initial

state. We observe that the electrons and positrons can

transmit through each other in this regime with a fairly high

probability. We also study the dynamics of the model with

OBC. Flux unwinding cannot occur with OBC, but our

simulations clearly show that positive and negative charges

can transmit through each other with high probability.

Finally, we study the time-evolution of the zero-electric

field ground state and show that Schwinger pair production

occurs and leads to flux unwinding.

This paper is structured as follows. In Sec. II we review

the discrete version of the Schwinger model. In Sec. III we

describe our numerical techniques, the initial states we will

consider, and the observables we will compute. In Sec. IV

we present our results, and in Sec. V we conclude.

II. THE SCHWINGER MODEL ON A LATTICE

The Hamiltonian for the continuum Schwinger model is

that of quantum electrodynamics (QED) in one spatial

dimension [1,16,17]

H ¼



−i

ψγ



þ igA



ψ þ m

ψψ þ



: ð1Þ

We work in natural units with c ¼ ℏ ¼ 1. Here E is the

electric field operator, the vector potential A

is related to

the electric field by E ¼ −

because we choose the gauge

¼ 0, ψ is the two component field operator for the

electrons and positrons,

ψ ¼ ψ

†

, m is the mass of the

electron, g is the charge. The γ

matrices of dimension

2 × 2 are defined by fγ

; γ

g¼2η

μν

where η

μν

is the

Minkowski metric with diagonal elements of ð−1; 1Þ and

zero otherwise. The indices μ, ν run from 0 to 1. Note that

the charge g has dimensions of mass, as does the electric

field E.

In one spatial dimension, Gauss’ law takes the form

EðyÞ¼F þ g

ðy

Þð2Þ

where j

¼ ψ

†

ψ and F is a constant background electric

field at the position y ¼ 0. The nature of Gauss’ law in one

dimension is that the electric field is constant when the

charge density is zero, and changes by g across the position

of a charge g.

FIG. 1. Schematic representation of the dynamics of a pair

particle-antiparticle under an external electric field (quench) α.

The electric field accelerates the fermions in opposite directions,

lowering the average electric field on each circuit.

NAGELE, CEJUDO, BYRNES, and KLEBAN PHYS. REV. D 99, 094501 (2019)

094501-2

剩余8页未读，继续阅读

评论收藏

内容反馈

weixin_38685521

粉丝: 4
资源: 935

晶格Schwinger模型中的助焊剂展开

非交换Schwinger模型中光子极结构的研究

对偶公式中无质量晶格Schwinger模型的仿真策略

倒装晶片的组装的助焊剂工艺

全息模型中的Schwinger效应和负微分电导率

用对偶公式求解无质量格Schwinger模型的符号问题。

动态辅助的Schwinger效应及其全息扩展与强耦合

基础电子中的助焊剂的作用

有限θ时的大规模Schwinger模型

具有D0–D4背景的Witten–Sakai–Sugimoto模型中的电磁不稳定性和Schwinger效应

电荷q多味Schwinger模型中的分数θ角，不是Hooft异常和量子子

带有耦合Schwinger-Dyson方程组的Technicolor模型

倒装晶片装配对助焊剂应用单元的要求

具有Faddeevian异常的手性Schwinger模型及其BRST量化

异常匹配，（轴向）Schwinger模型和高T超级Yang-Mills畴壁

Flux-env:助焊剂

助焊剂入门

通过使用有噪声的中尺度量子计算的内插器优化来加速晶格量子场理论计算

taylor展开

助焊剂

助焊剂入门：fluxcd

lcars:排队的助焊剂分派器

Schwinger-Thirring模型中的弦张力和约束性质的鲁棒性

react:连接助焊剂起React

Wear张量的对应Rarita-Schwinger类型字段

Schwinger模型相对论

Schwinger效应影响原始磁生成

Schwinger效应对原始光谱的影响

最新资源