没有合适的资源?快使用搜索试试~ 我知道了~
针对单个圆进行视觉测量存在的位姿二义性问题,提出了一种运动重建约束角的二义性消除方法。在相机已标定的前提下,利用圆的投影椭圆曲线确定圆的位姿参数,位姿存在二义性;利用多视图从运动恢复结构方法估计特征点的世界坐标,并利用特征点重建约束角;基于刚体运动不改变空间夹角的特性同时唯一确定多视图的圆位姿。仿真结果显示:在500 mm距离内,噪声强度为0.4 pixel时二义性消除成功率为100%,强度为1 pixel时成功率约为93%;噪声强度为0.1 pixel,距离在1000 mm 时具有99.6%的成功率。此外,在二视图的情形下算法的平均运行时间约为5ms,适合实时性的应用。该方法不需要目标的额外信息,能够实时有效地消除圆位姿的二义性。
资源推荐
资源详情
资源评论

第 36 卷 第 1 期
2016 年 1 月
Vol. 36, No. 1
January, 2016
光 学 学 报
ACTA OPTICA SINICA
0115002-
运动重建约束角的圆位姿二义性消除方法
张李俊 黄学祥 冯渭春 胡天健 梁书立
北京跟踪与通信技术研究所, 北京 100094
摘要 针对单个圆进行视觉测量存在的位姿二义性问题,提出了一种运动重建约束角的二义性消除方法。在相机已
标定的前提下,利用圆的投影椭圆曲线确定圆的位姿参数,位姿存在二义性;利用多视图从运动恢复结构方法估计特
征点的世界坐标,并利用特征点重建约束角;基于刚体运动不改变空间夹角的特性同时唯一确定多视图的圆位姿。
仿真结果显示:在 500 mm 距离内,噪声强度为 0.4 pixel 时二义性消除成功率为 100%,强度为 1 pixel 时成功率约为 93%;
噪声强度为 0.1 pixel,距离在 1000 mm 时具有 99.6%的成功率。此外,在二视图的情形下算法的平均运行时间约为 5
ms,适合实时性的应用。该方法不需要目标的额外信息,能够实时有效地消除圆位姿的二义性。
关键词 机器视觉; 圆; 位姿估计; 二义性; 角度约束; 从运动恢复结构
中图分类号 TP242.6 文献标识码 A
doi: 10.3788/AOS201636.0115002
Solution of Duality in Pose Estimation of a Single Circle
Utilizing Constraint Angles Motion Reconstruction
Zhang Lijun Huang Xuexiang Feng Weichun Hu Tianjian Liang Shuli
Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China
Abstract In order to cope with the pose duality problem in the visual measurement of a single circle, a
disambiguating approach is proposed utilizing constraint angles motion reconstruction. On the premise of camera
calibrated, the pose parameter of a circle is estimated from its projected ellipse curve but the pose has duality. The
world coordinates of feature points are recovered by the method of multiple view structure from motion and
constraint angels are reconstructed with feature points. Based on the nature that rigid body motion does not change
space angles, the poses of multiple view are determined simultaneously. Experimental results indicate that within
the range of 500 mm the circle radius, the success rate of eliminating false solution is up to 100% when the noise
level is within 0.4 pixel and 93% when the noise level is 1 pixel. And the success rate is 99.6% when the noise level
is 0.1 pixel and the range is 1000 mm the circle radius. Besides, the average run time of the proposed algorithm in
two views is about 5 ms which suits real-time application. The proposed approach can effectively identify real poses
of a single circle in real time without any additional information of target.
Key words machine vision; circle; pose estimation; ambiguity; angular constraint; structure from motion
OCIS codes 150.0155; 120.1880; 110.5200
1 引 言
利用自然特征测量目标本体坐标系与相机坐标系间相对位姿关系,在增强现实
[1]
、相机标定
[2]
、视觉跟踪
[3]
以及视觉 测量
[4-5]
等机器视 觉领域中 有广泛应用。圆是一类常见的自然特征,在自然景物和人造物体中大
量存在 ,比如道路旁圆形的指示 牌,用于 相机标 定的圆形靶标物,空间飞行器上 的星箭 对接环、推进器 喷管
管口等。相较于点线特征,基于圆的视觉位姿估计有很多的优势,如需要的特征数目少、具备一定的抗遮挡
能力、特征识别容易等。
收稿日期: 2015-06-05; 收到修改稿日期: 2015-09-10
基金项目: 国家自然科学基金(11402004)
作者简介: 张李俊(1991—),男,硕士研究生,主要从事机器视觉和视觉测量方面的研究。E-mail:zljun@mail.ustc.edu.cn
导师简介: 黄学祥(1970—),男,副研究员,硕士生导师,主要从事空间操作方面的研究。E-mail:h_xxiang@163.com
1
光 学 学 报
0115002-
基于分析几何的单个圆位姿闭式解
[6-7]
具有二义性,其中一个为真实解,另一个为虚假解,从位姿中找出
真实解对于实际的应用非 常重要。为了消 除解的二义性,文 献[8]提出 当目标为 圆柱体时,利用圆柱体的两
条母线可以消除圆的二义性;文献[9]指出,若圆的半径已知并能在像平面识别圆心的投影点,则圆的位姿可
以唯一确定;文献 [6]提出对于同时 存在多个圆且法 向量相同的情形 ,可以将法向量平 行作为约 束来消除二
义性;文献[10]提出当圆平面上存在直线对时,可以利用直线对的角度约束消除二义性;文献[11]利用圆平面
上圆外 侧参考 点到圆 心距离 的欧式 不变性 作为约 束消除 位姿的 二义性 。以上 方法或 是要求目标存在特殊
的结构,或是需要 目标额外的可识 别的特征 ,当场景 不满足要求时,方 法将不再适用。 文献[12]利用激光 测
距仪的距离信息消除解的二义性,该方法不需要目标具备特殊的结 构或额 外的特 征信息 ,但需要 其他测 量
设备辅助,增加了额外的成本。
针对圆位姿二义性问题,本文讨论了一种在无先验信息条件下,利用刚体运动不改变空间夹角的角度约
束来消除单个圆位姿二义性问题的方法。利用两次成像得到的圆投影椭圆计算出各自相机系下圆位姿解和
对应的圆法向量,利用每次成像提取共同的目标特征点,基于从运动恢复结构的方法解算特征点的世界坐标
和两次成像相机的外参数。再从特征点中选择一组特征点对,利用点对的世界坐标和两次成像相机的外参数
分别计算特征点对两个相机系中的相机系坐标,得到特征点对连线的方向向量。计算每次成像圆法向量与特
征点对连线方向向量的夹角,基于刚体运动不改变空间夹角的角度约束,唯一确定每次成像圆的位姿。
2 基于空间圆投影的位姿估计方法
2.1 空间圆的位姿表示
不失一般性,所有的讨论均假设相机已完成标定,并在成像过程中内参数保持不变。
基于圆的位姿参数有圆心的三维坐标和圆平面的法向量。单个圆具有旋转不变性,只能确定圆的两个
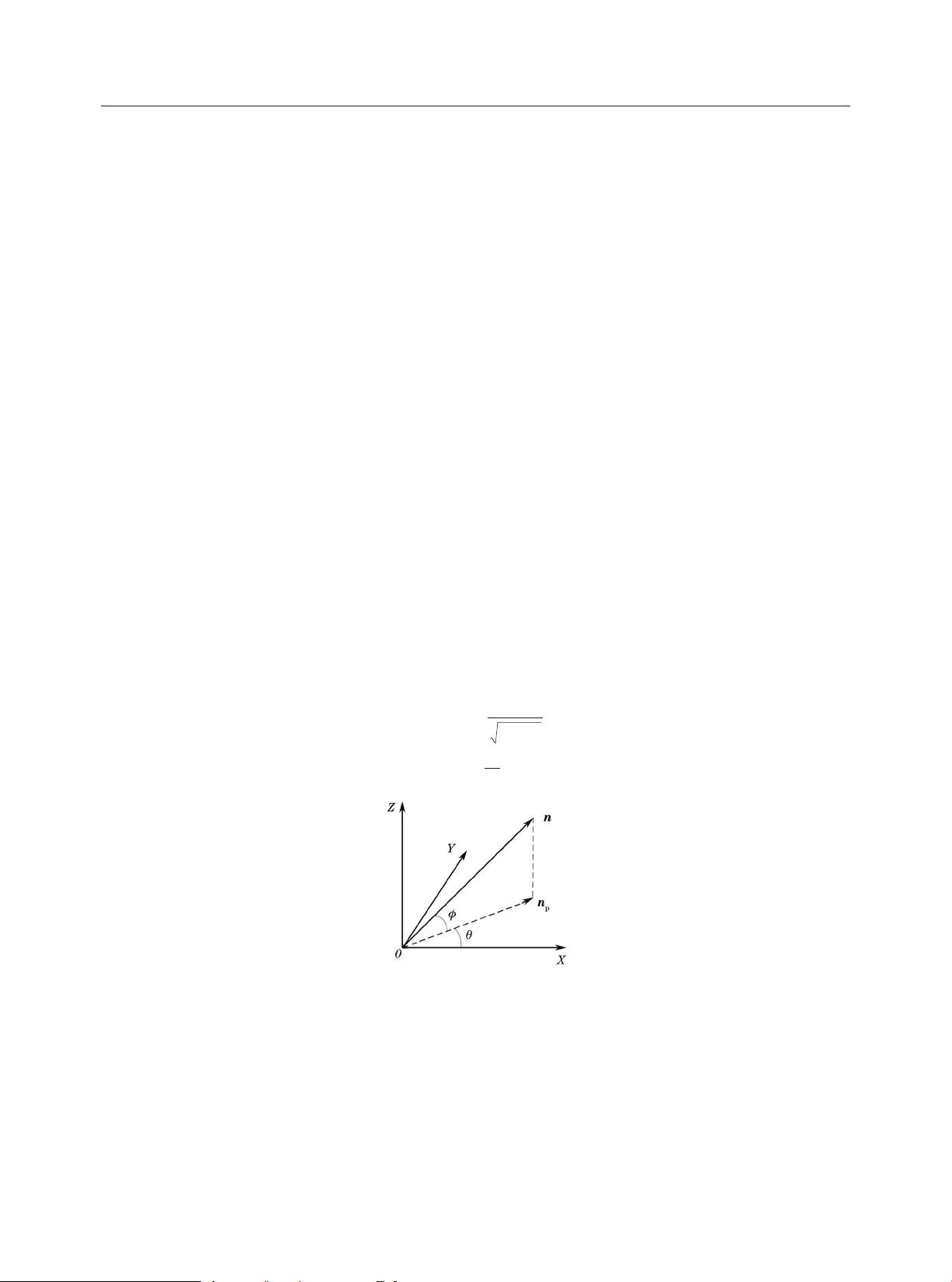
姿态角,分别是俯仰角和偏航角。如图 1 所示,设 n 为三维空间中圆平面的法向量,在坐标系 O-XYZ 下,n 对
应的姿态角分别为俯仰角
ϕ
和偏航角
θ
。俯仰角
ϕ
定义为法向量 n 与 XOY 平面的夹角,偏航角
θ
定义为法
向量 n 在 XOY 平面上的投影向量 n
p
与 OX 轴正向的夹角。当已知圆平面法向量 n=(n
x
,n
y
,n
z
),则俯仰角
ϕ
和偏
航角
θ
分别为
ì
í
î
ï
ï
ï
ï
ϕ = arctan
n
z
n
2
x
+ n
2
y
θ = arctan
n
y
n
x
. (1)
图 1 圆姿态参数定义
Fig.1 Definition of circle pose parameters
2.2 坐标系定义与成像模型
图 2 坐标系关系中,O
C
-X
C
Y
C
Z
C
为相机坐标系,O-UV 为图像像素坐标系,o-xy 为归一化焦距平面坐标系。
相机成像采用常见的针孔成像模型,相机坐标系下的三维点 P
C
(X
C
,Y
C
,Z
C
)与像点的图像像素坐标 p(u,v)之
间的关系采用齐次坐标表示为
Z
C
p = KP
C
, (2)
式中 K 为相机的内 参数矩阵,它描述了 相机坐标系 与图像像素 坐标系之间 的映射关系 。为了 计算 的需要 ,
2
剩余9页未读,继续阅读
资源评论

weixin_38677472
- 粉丝: 3
- 资源: 967
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功