没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
Introduction to Mathematics for Game Development.James Cowley(Dated: June 23, 2016)2I. INTRODUCTIONThis article is intended as an introduction to all the basic mathematical concepts you will needto understand for game development. It will make the assumption that you are someone whomaybe was never particularly good at maths, or who took maths classes so long ago that you canbarely remember them. Basically, I will not assume much prior knowledge of mathematics.This guide obviously has it’s limita
资源推荐
资源详情
资源评论

Introduction to Mathematics for Game Development.
James Cowley
(Dated: June 23, 2016)

2
I. INTRODUCTION
This article is intended as an introduction to all the basic mathematical concepts you will need
to understand for game development. It will make the assumption that you are someone who
maybe was never particularly good at maths, or who took maths classes so long ago that you can
barely remember them. Basically, I will not assume much prior knowledge of mathematics.
This guide obviously has it’s limitations; I will not be going into massive depth on any of these
subjects, or treating them with a high degree of rigour. So if you want to get some more details on
any of the topics introduced here, I’ll be providing a reference list at the end.
I’ll wrap up this section with a little bit about myself. I am currently studying physics at
university, in my third year, so maths is like a second language to me (I’m not very good at learning
actual languages, though, unfortunately). I want to go into full-time game development once I
graduate, so I’ve been programming in my spare time, and there are a lot of cases where I have
come across other devs saying “I wish I understood matrices” or “what the hell is a quaternion?”.
So I decided to make this in the hopes that it would help someone out at some point.
Now, on to the meat of the article.
II. TRIGONOMETRY
I’m sure many of you have traumatic memories of high school trigonometry lessons. That is
fair enough, but trig lies at the heart of a large amount of game development, and maths as a whole.
So you are going to have to take this bull by the horns at some point. I will try to cover it in as
nice a way as possible, though.
Firstly: what is trigonometry? Well, it ultimately stems from the study of geometry, specifically
triangles. The overall idea is to relate angles to distances and vice versa. There are many different
trigonometric quantities, but there are six that you need to know about: sin, cos, tan, arcsin,
arccos, and arctan. They may sound very intimidating, but in reality they are pretty simple, if you
have a diagram to help, that is. If you turn your attention to Figure 1, you will see a construction
called the “unit circle”. The word “unit” is one that crops up all the time in maths; it basically
means “length = 1”. So the unit circle is a circle with a radius of one. Specifically “THE” unit
circle is the circle with radius one, and centred at the origin of whatever coordinate system you are
dealing with.
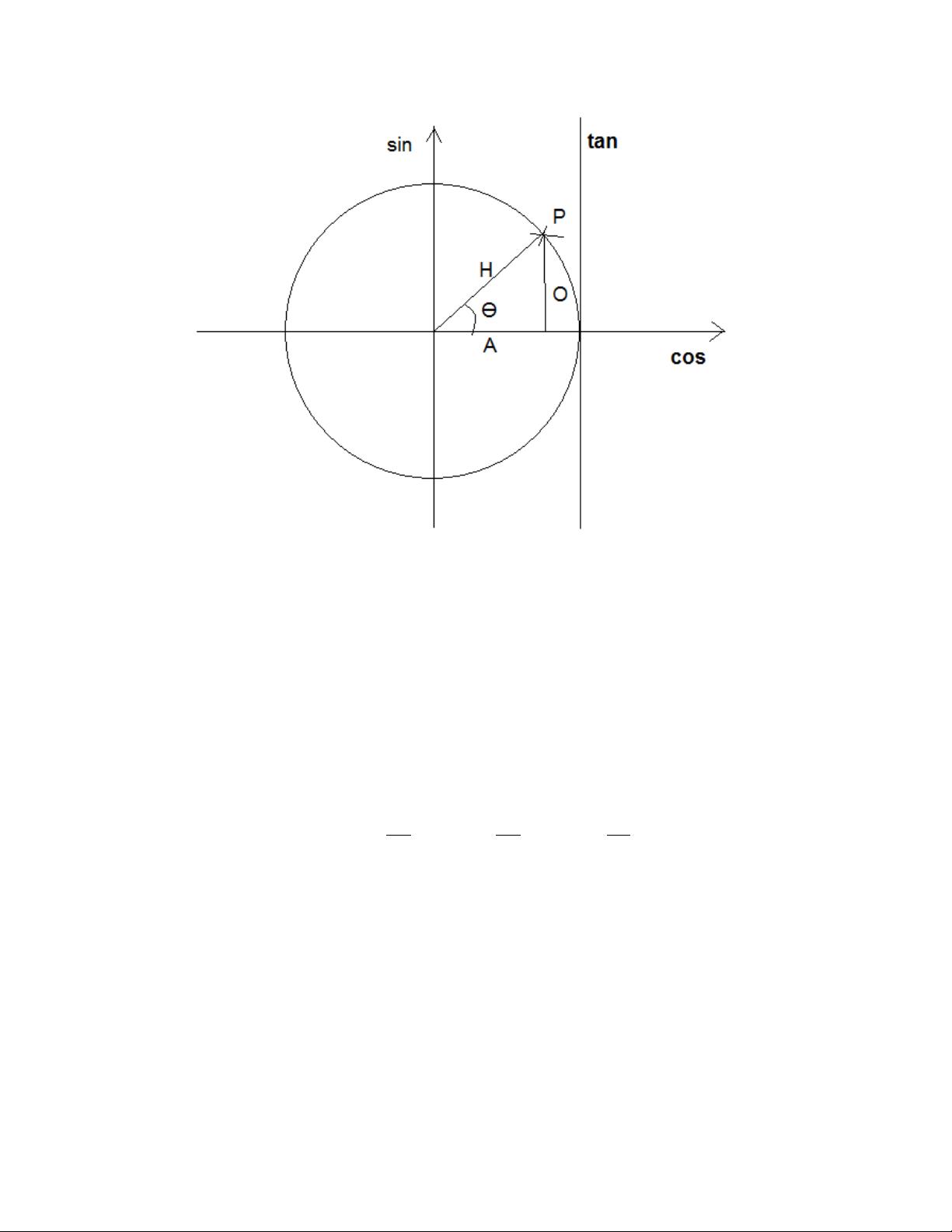
3
FIG. 1. The unit circle for trigonometry.
Let us take a look at that triangle marked on the figure. You can see the sides are marked “O”,
“H” and “A”. These stand for “Opposite”, “Hypotenuse” and “Adjacent”. So the “opposite” side
is opposite the angle θ, the “adjacent” side is next to it, and the “hypotenuse” is the longest side.
You may recall being taught in school the “SOH CAH TOA” mnemonic. That is simply a way to
remember the following relations:
sin(θ) =
L
O
L
H
, cos(θ) =
L
A
L
H
, tan(θ) =
L
O
L
A
. (1)
where L
A
, L
O
, L
H
are the lengths of each side of the triangle. If you bear these in mind, and
then look back at the unit circle, you will see that I have marked the y-axis as “sin” and the x-axis
as “cos”. This is because the y coordinate of a point P on the circle is equal to the sin of the angle
θ; this is easy to see, if you remember that the hypotenuse here is the radius of the circle, which is
just 1.
You will also notice a line marked “tan”. Tan is the short name for “tangent”; a tangent is a
line which joins a curve (in this case our unit circle) at one point only (in this case, (1, 0)). So if
sin(θ) is the y coordinate of the point P on the circumference, and cos(θ) is the x coordinate, then
what is tan(θ)? Well, that is the y coordinate of the point at which our line touches the tangent
剩余16页未读,继续阅读
资源评论

weixin_38675341
- 粉丝: 8
- 资源: 998
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 《孙权劝学》教学设计与反思.docx
- 《土地的誓言》教学设计与反思.docx
- 《老山界》课程设计及反思.docx
- 《黄河颂》教学方案及反思.docx
- 基于java+springboot+vue+mysql的技术交流和分享平台 源码+数据库+论文(高分毕业设计).zip
- 《诫子书》教学设计.docx
- 《散步》教学设计.docx
- 《小圣施威降大圣》教学设计.docx
- 《狼》教学设计.docx
- 《我的白鸽》教学设计.docx
- 《大雁归来》教学设计及反思.docx
- 《猫》教学设计.docx
- 《秋天的怀念》教学设计.docx
- 《雨的四季》教学设计.docx
- 《春》教学设计.docx
- 《散步》教学设计及课堂流程.docx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功