液氩体积中微子相互作用重构的局部主曲线算法的实现资源-CSDN文库

25 浏览量 2020-03-23 03:11:14 上传评论收藏 1.45MB PDF 举报

液氩体积中微子相互作用的自动化跟踪与重建是高能物理实验中一个非常重要的研究方向。在本文中，研究人员介绍了一种新的局部主曲线算法，该算法能够在三维空间中对液态氩时间投影室（LAr-TPC）内的中微子相互作用进行追踪和“淋浴”重建。这里的“淋浴”指的是高能粒子与物质相互作用后产生的次级粒子簇射。LAr-TPC是一种探测器技术，它能够对中微子相互作用产生的粒子进行同时跟踪和量热测量，具有极高的空间分辨率。局部主曲线（Local Principal Curves, LPC）算法是一种用于处理多维数据的分析工具，能够在高维空间中找到数据的底层结构。它是主曲线（Principal Curves）算法的一个变种，主曲线是一种通过数据集的“中心”来描述数据分布的非线性推广。LPC算法与全局主曲线算法相比，更加关注数据的局部特征，对于处理中微子相互作用产生的复杂数据更加有效。文章中提及的“模拟数据集”是指在计算机上通过模拟实验过程产生的数据集。这些数据集被用来表征和验证算法性能，即算法在处理真实数据之前，先在模拟环境中测试其准确性和效率。文章提到的“LAr-TPC”探测器正在欧洲、日本和美国的多个研发计划中开发，这些探测器被认为是满足下一代中微子振荡实验物理需求的探测技术。中微子振荡实验主要研究中微子在不同“味道”（中微子类型）之间的转换现象。LAr-TPC可以提供从极低到极高能量范围内中微子相互作用产生的粒子的跟踪和量热测量，具有极高的空间分辨率。例如，ICARUS实验就展示了这种探测器技术的精细分辨能力。文章中提到的“电离轨迹”是指带电粒子在液氩介质中运动时释放出的电离电荷，这些电荷可以被TPC测量，从而提供粒子在空间中的三维轨迹。这些轨迹数据可以表示为一系列的“击中点”，每个点包含了空间单元坐标信息（x, y, z）以及相应的电荷或能量沉积Q。文章中还提到了多个机构与人员，例如英国华威大学物理系和杜伦大学数理科学系的研究人员。这表明这项研究是跨学科合作的成果，涉及物理实验和数理统计分析等多个方面。文章中的DOI编号（10.1140/epjc/s10052-014-2832-4）是用来唯一标识这篇科学论文的数字对象标识符，便于在学术数据库中检索和引用。而EUR.Phys.J.C则是《欧洲物理期刊C辑》（European Physical Journal C），是一本物理学领域的同行评审学术期刊，发表与高能物理相关的研究论文。本文的研究内容涉及了粒子物理学中探测器技术、数据分析方法以及高能物理实验的数据处理技术。局部主曲线算法的实现及其在模拟数据集上的性能测试对于自动重构中微子相互作用具有重要的理论和实验意义。

资源推荐

资源详情

资源评论

Eur. Phys. J. C (2014) 74:2832

DOI 10.1140/epjc/s10052-014-2832-4

Special Article - Tools for Experiment and Theory

Implementation of a local principal curves algorithm for neutrino

interaction reconstruction in a liquid argon volume

J. J. Back

1,a

, G. J. Barker

,S.B.Boyd

, J. Einbeck

, M. Haigh

, B. Morgan

, B. Oakley

, Y. A. Ramachers

D. Roythorne

Department of Physics, University of Warwick, Coventry CV4 7AL, UK

Department of Mathematical Sciences, Durham University, Durham DH1 3LE, UK

Received: 23 December 2013 / Accepted: 19 March 2014 / Published online: 29 March 2014

Abstract A local principal curve algorithm has been imple-

mented in three dimensions for automated track and shower

reconstruction of neutrino interactions in a liquid argon time

projection chamber. We present details of the algorithm and

characterise its performance on simulated data sets.

1 Introduction

Liquid argon time projection chambers (LAr-TPCs), that are

currently in development in various R&D programmes in

Europe, Japan and the USA [1], are acknowledged to be a

detector technology capable of meeting the physics require-

ments of a next-generation neutrino oscillation experiment.

They can provide simultaneous tracking and calorimetry of

particles from neutrino interactions over a wide range of ener-

gies, with exquisite millimetric granularity, as demonstrated

by results from ICARUS [2]. Despite this advantage, it has

proven difﬁcult to achieve an automated software process

that can fully reconstruct neutrino interactions, which will

contain a mixture of ionisation tracks as well as electromag-

netic and hadronic showers, especially when the neutrino

interaction point is not known beforehand. In this paper, we

describe a ﬁrst application of using local principal curves

[3] to automatically reconstruct neutrino interactions using

three-dimensional LAr-TPC data.

When a charged particle passes through a liquid argon

medium it releases a stream of ionisation charge which can

be measured by a TPC to provide a 3D trajectory in space. We

can represent this data as a collection of “hits”, each of which

contain the spatial cell co-ordinate information (x, y, z)as

well as the charge or energy deposit Q. The task of any

reconstruction algorithm is to ﬁrst obtain the hits from the

detector output, then group these hits into clusters in order to

e-mail: j.j.back@warwick.ac.uk

identify the particles coming from the neutrino interaction,

before extracting physics parameters such as momentum or

energy from the reconstructed particles. Here, the ﬁrst stage

of the analysis chain, hit reconstruction, is assumed to have

already taken place and the input is taken to be the complete

set of hits in three spatial dimensions. Our reconstruction

algorithm takes the collection of hits for each neutrino inter-

action (labelled as an event) and forms clusters of associated

hits in order to identify the particles. The mathematics and

logic behind the local principal curve procedure is described

in Sect. 2, while a description of the simulation methods

used to obtain samples of neutrino interaction events in liquid

argon is given in Sect. 3. The performance of the reconstruc-

tion algorithm is discussed in Sects. 4 and 6, with details

about using it for track-shower discrimination provided in

Sect. 5. Finally, we summarise our ﬁndings in Sect. 7.

2 The local principal curve (lpc) algorithm

The key component of the method we are proposing is the

mean shift procedure, a versatile tool which is popular mainly

in the computer vision community [4]. In essence, the mean

shift moves a point to the local mean of the data around this

point. For our case, the points are the positions X

(x, y, z) of

all of the hits, which are each scaled by their range, deﬁned

to be the difference between the largest and smallest values

of X

(though it is also possible not to scale at all, or to scale

by other measures of spread such as the standard deviation).

The local mean m(u) for a set of N hits is deﬁned as

m(u) =



i=1

(u)X



i=1

(u)

, (1)

where t he weights w

(u), which determine the size and shape

of the local neighbourhood at a chosen location u, are mono-

123

2832 Page 2 of 15 Eur. Phys. J. C (2014) 74:2832

tonically decreasing with increasing distance from u to X

common choice of weights is the Gaussian density function

(u) =

(2π)

3/2

exp



−

− u)



, (2)

where Q

is the energy deposit for hit i and h is a constant

bandwidth parameter that steers the size of the local neigh-

bourhood. The weights play the role of “kernel” functions

and can, if desired, be replaced by other functions such as a

triangular-shaped or truncated probability density. In our sce-

nario, where the co-ordinates are all measured on the same

scale, we keep the Gaussian form and use the same band-

width parameter for all three directions. The value of h can

be selected through a coverage measure [3], though for our

purposes there is not much reason for this, as roughly the

same bandwidth, h ∼ 0.05 after scaling, will be usable in a

wide range of liquid argon detectors. Note that the normal-

isation denominator (2π)

3/2

can be left out of the kernel

function since it is a constant common factor for all hit points

and has no effect on the properties of the principal curve.

From Eq. 1, we deﬁne the mean shift as

s(u) = m(u) − u =



i=1

(u)(X

− u)



i=1

(u)

. (3)

This quantity has many interesting properties [4], one

of which being that s(u) ∝∇

f (u)/

f (u), where

f (u) =



i=1

(u) is a density estimate of f at u. This implies

that the mean shift is a vector pointing into a denser direc-

tion of the data space. When carried out iteratively, starting

at u = m

, one can show [4] that the series of local means

+1

= m



+ s(m



),  ≥ 0, (4)

converges to a local mode u

f (u) where s(u

) = 0. This

has the attractive property of being a clustering technique; a

trajectory can be formed by running the mean shift proce-

dure on each data point X

iteratively until convergence is

achieved.

Though the convergence towards a local mode of the den-

sity is an appealing property, it has the negative side effect of

getting trapped at the local modes and will not move beyond

them. Therefore, some modiﬁcation of Eq. 4 is needed which

ensures that particle trajectories are pursued beyond local

modes. The simple idea is to alternate the mean shift with

a local principal component step [3]. More speciﬁcally, let

γ(u) be the normalised eigenvector corresponding to the

largest eigenvalue of the local symmetric 3 × 3 covariance

matrix

(u) =



i=1

(u)



i=1

(u)(X

− u)(X

− u)

. (5)

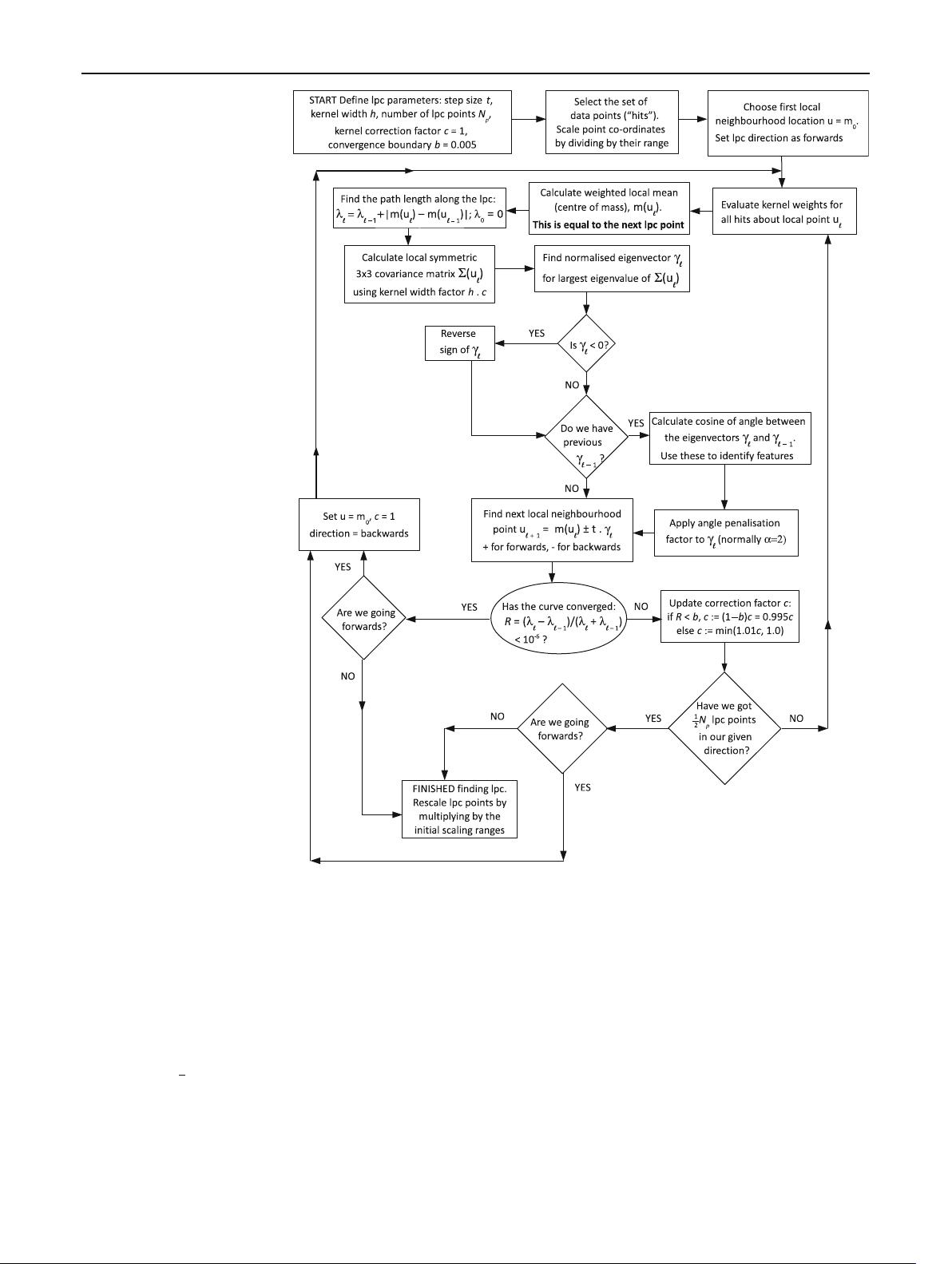
Starting from a given point u = m

,weset = 0 and iterate

between

1. computing the local centre of mass:

m(u



) ≡ u



+ s(u



); (6)

2. ﬁnding the next local neighbourhood location:

+1

= m(u



) + t × γ



, (7)

where t is a given step size (of the same order as h) and



≡ γ(u



). The local principal curve is then deﬁned as the

series of local centres of mass m(u



). In our case, the starting

point u = m

is chosen to be the position of the nearest hit to

the energy-weighted centroid of all of the hits. Alternatively,

can be set either at random from the X

points, set by

hand, or be chosen to be a local density mode using an initial

mean shift procedure as outlined in Refs. [3,5]. The above

iteration is repeated until either the required number of lpc

points (N

) is obtained, or the path length along the local

curve is no longer increasing (convergence).

As we will see later, the angle φ between the normalised

eigenvector γ



and the preceeding eigenvector γ

−1

can be

used to infer the presence of feature points, corresponding

to drops in the angle proﬁle along the principal curve, which

provide evidence for particle decays or possible interactions

between particles.

In order to provide inertia for reducing the chance of the

local principal curve deviating too much from the general

direction of neighbouring points, γ



is multiplied by an angle

penalisation term a =|cosφ|

, where α is usually set to 2,

when the next local neighbourhood location is found using

Eq. 7:



:= aγ



+ (1 − a)γ

−1

. (8)

A technicality to be mentioned is that, for a given (u),the

ﬁrst eigenvector may equally well be −γ(u) as well as γ(u),

so for each  ≥ 1, one needs to check whether cosφ>0 and

set γ



:= −γ



otherwise [3].

Based on asymptotic considerations [5], it can be shown

that the sequence of lpc points m(u



) converges to a point

close to the boundary of the cloud of data points with

the property f (u

) = h|∇

f (u

)|. In practical terms, conver-

gence is reached when the cumulative path length difference

between neighbouring local curve points, divided by their

sum, is below a chosen threshold typically set at 10

−6

R =



− λ

−1



+ λ

−1

< 10

−6

, (9)

where λ



= λ

−1

+|m(u



) − m(u

−1

)| and λ

= 0. In

order to pick up features that may be present in the tails

123

剩余14页未读，继续阅读

评论收藏

内容反馈

weixin_38663036

粉丝: 4
资源: 928

液氩体积中微子相互作用重构的局部主曲线算法的实现

基于局部体积最大的轮廓线三维形体重构算法 (2011年)

有效场论视角下的一般中微子相互作用

液态氩中微子实验中的带电粒子

非标准中微子相互作用：现状和未来展望

暗物质实验中太阳中微子的非标准相互作用

水在中性电流中微子相互作用中单个π0生产率的测量

在Hyper-K探测与超新星中微子的非标准中微子相互作用

非单一性，无菌中微子和非标准中微子相互作用

核中微子相互作用中的质子-质子相关性

减少非标准中微子相互作用中的阴暗面

DUNE的非标准中微子相互作用

中微子自相互作用暗物质在焦点超对称中的实现

根据对撞机和中微子望远镜数据的暗物质-中微子相互作用

通过比较超新星中微子的带电和中性电流相互作用速率来探测中微子质量等级

中微子-核子相互作用中的单个介子产生

R K难题和非标准中微子相互作用的光Z′

中微子的张量和标量相互作用可能导致可观察到的中微子磁矩

使用COHERENT能量和定时数据改进了对非标准中微子相互作用的整体拟合

模糊暗物质和非标准中微子相互作用

非标准中微子-核相互作用中的中微子跃迁磁矩

中微子非标准相互作用的一般相干约束

DUNE的源，探测器和物质非标准中微子相互作用的综合研究

从中微子-氘核反应数据中提取的最终状态相互作用对中微子-核子介子产生截面的影响

NLO的热中微子相互作用速率

环诱导的中微子非标准相互作用

在COHERENT数据后测试具​​有任意介体质量的大型非标准中微子相互作用

在暗物质探测器中搜索BSM中微子相互作用

最新资源

在COHERENT数据后测试具有任意介体质量的大型非标准中微子相互作用