没有合适的资源?快使用搜索试试~ 我知道了~
为了满足对电网非平稳扰动信号快速、准确分析的要求,提出了一种采用奇异值梯度信息的暂态电能质量扰动检测新方法。通过滑动窗奇异值分解(SVD)方法提取信号的变化特征、降低噪声干扰,并通过奇异值梯度求取扰动指示信号,得到初步定位结果。提出无参自适应阈值,进一步抑制噪声干扰并实现对暂态扰动信号的检测定位。所提算法原理简单,无需进行前置滤波及参数调节。一系列仿真试验的对比分析结果表明,所提算法定位准确、抗干扰能力强,对过零点扰动也有较好的检测效果。通过对变电站实际暂态扰动数据的检测分析,进一步验证了所提算法的有效性。
资源推荐
资源详情
资源评论

第 39 卷 第 6 期
2019 年 6 月
电 力 自 动 化 设 备
Electric Power Automation Equipment
Vol.39 No.6
Jun. 2019
采用奇异值梯度信息的暂态电能质量扰动自适应检测方法
杨晓梅
1
,郭朝云
1
,樊 博
2
,罗月婉
1
,肖先勇
1
(1. 四川大学 电气信息学院,四川 成都 610065;2. 国网宁夏电力有限公司电力科学研究院,宁夏 银川 750011)
摘要:为了满足对电网非平稳扰动信号快速、准确分析的要求,提出了一种采用奇异值梯度信息的暂态电能
质量扰动检测新方法。 通过滑动窗奇异值分解( SVD)方法提取信号的变化特征、降低噪声干扰,并通过奇异
值梯度求取扰动指示信号,得到初步定位结果。 提出无参自适应阈值,进一步抑制噪声干扰并实现对暂态扰
动信号的检测定位。 所提算法原理简单,无需进行前置滤波及参数调节。 一系列仿真试验的对比分析结果
表明,所提算法定位准确、抗干扰能力强,对过零点扰动也有较好的检测效果。 通过对变电站实际暂态扰动
数据的检测分析,进一步验证了所提算法的有效性。
关键词:暂态电能质量;扰动检测;奇异值分解;奇异值梯度;自适应阈值;抗噪性
中图分类号:TM 761 文献标志码:A DOI:10.16081 / j.issn.1006
-
6047.2019.06.020
收稿日期:2018
-
09
-
18;修回日期:2019
-
04
-
19
0 引言
现代电力电子设备不仅自身对扰动敏感,同时
也会产生扰动,从而影响其他用户
[1]
。 所以随着电
力电子设备的大量投入使用,电能质量扰动问题日
益严重。 目前,短 时傅里叶 变换 STFT( Short⁃Time
Fourier Transform)、小波变换 WT(Wavelet Transform)、
S 变换、希尔伯特变换 HT(Hilbert Transform) 等信号
分析技术在电能质量扰动检测方面得到了广泛的应
用,但这些方法及其改进方法都存在各自的不足:
STFT 的加窗面积固定,分辨率单一,不适用于对非
平稳信号的扰动检测
[2]
;WT 需要人为选择小波基
函数及分解尺度,检测效果存在较大的差异,无法保
证最优分解效果
[3]
;S 变换的运算量大且窗函数不
能依据具体的情况进行调整,缺乏灵活性
[4]
;HT 运
用到工程实践中还需要解决端点效应、模态混叠等
问题
[5⁃6]
。
近年来,基于形态学、奇异值分解 SVD(Singular
Value Decomposition)的检测方法取得了一定的研究
成果,此类方法从波形特征出发,结合加窗及软阈值
实现实时扰动定位,算法原理简单,运算速度快。 文
献[7]利用短窗功率算法,对形态滤波后的信号进
行加窗并计算窗内信号能量,通过能量变化判断是
否发生扰动,但该方法未明确指出如何实现自动定
位扰动,且未分析窗宽对算法的影响。 文献[8] 利
用差分思想并结合局部分析窗提取信号突变信息,
通过自适应阈值对扰动进行检测定位,该算法无需
前置滤波,且抗噪性能较好。 但该方法的阈值参数
及局部分析窗的半径需通过实验确定,且关于阈值
参数并未给出选取依据。 文献[9]利用在 Hankel 矩
阵方式下 SVD 与小波分解的机理相似,对扰动信号
构造 Hankel 矩阵进行 SVD,并通过分量信号检测扰
动。 上述方法的计算量小,且对谐波干扰不敏感。
但基于 SVD 的方法的抗噪性较差,在弱扰动情况下
无法检测过零点扰动。 且文献[9] 中的阈值设置简
单,仅将阈值参数设为分量信号 P
3
最大值的 30%,
由于扰动起止时刻是随机的,这使得 P
3
峰值相差很
大,会出现扰动检测失效及误检的情况。 文献[10]
将滑动窗 SVD 与集合经验模态分解 ( EEMD) 相结
合,通过 SVD 重构本征模态函数(IMF) 分量矩阵来
压缩数据量,并通过 HT 进行降维,该方法改善了模
态混叠现象 并 提高了特 征提取的 准 确性,但采 用
EEMD 方法进行特征提取过程中存在的计算量较大
的问题未得到解决。
针对上述问题,本文通过滑动窗 SVD 及奇异值
梯度变化提取信号扰动时刻的奇异性特征,相较于
传统时频特征提取方法,该方法的计算量小、实时性
更强;并结合无参自适应阈值完成扰动信号的检测、
定位。 通过实验分析与算法的对比分析验证了所提
方法的准确性及优越性。
1 本文所提扰动检测算法
1.1 滑动窗 SVD
SVD 是指:对于任意一个实矩阵 A∈R
m ´ n
,必定
存在正交矩阵 U
=
[u
1
,u
2
,…,u
m
] ∈R
m ´ m
和正交矩
阵 V
=
[v
1
,v
2
,…,v
n
]∈R
n ´ n
使得式(1)成立。
A
=
UΔV
T
(1)
其中,Δ
=
[diag(σ
1
,σ
2
,…,σ
q
),O] ∈R
m
×
n
为对角矩
阵,O 为零矩阵,q
=
min( m,n),σ
j
( j
=
1,2,…,q) 为
矩阵 A 的奇异值,且有 σ
1
≥σ
2
≥…≥σ
q
≥0。
利用 1 维信号可以构造多种矩阵,如 Toeplitz 矩
阵、Cycle 矩阵、Hankel 矩阵等,矩阵的构造方式不
同,则 信 号 通 过 SVD 后 的 效 果 也 不 同
[11]
。 文 献
[12]指出,在 Hankel 矩阵方式下,SVD 可保留信号
的波形特征,且与小波分解类似,当对整段信号进行
处理时,可对信号进行多分辨率分析。
第 6 期
杨晓梅,等:采用奇异值梯度信息的暂态电能质量扰动自适应检测方法
本文采用滑动窗的方法对被测信号进行实时检
测,依次对滑动窗内的信号进行 SVD 以提取信号特
征,为了保证提取出信号特征的同时减少计算量,对
滑动窗内的信号构造如下所示的 Hankel 矩阵 H
i
:
H
i
=
f(i) f(i
+
1) … f(i
+
w
-
1)
f(i
+
1) f(i
+
2) … f(i
+
w)
é
ë
ê
ê
ù
û
ú
ú
(2)
其中, f 为 1 维离散化待检测信号;i 为滑动窗的滑
动次数,i
=
1,2,…,K
-
w,w 为滑动窗的窗宽,K 为 f
的总采样点数。
本文所提算法中,窗宽 w
=
T / 2(T 为被测信号在
1 个周期内的采样点数)。 依据构造矩阵的特性,当
窗宽取为 T / 2 的整数倍时,由滑动窗获得的滑动奇
异信号构成直线,当信号中存在扰动时,滑动奇异信
号的幅值亦会随之改变,呈梯度性变化,从而通过滑
动奇异信号的幅值变化获得扰动信息。 但窗宽越
大,构造的矩阵越大,SVD 耗时越多,因此本文中窗
宽取为 T / 2。 窗宽 w 对本文所提算法的影响将在
3.1 节进行详细阐述分析。 下面介绍滑动奇异信号
的构造。
设滑动步长为 Δt(Δt 为采样时间间隔),运用式
(1)对 H
i
进行滑动窗 SVD,滑动窗每滑动 1 次可对
应得到 2 个奇异值 σ
i1
、σ
i2
,如式(3)所示。
H
i
=
U
i
Δ
i
V
T
i
=
σ
i1
u
i1
v
T
i1
+
σ
i2
u
i2
v
T
i2
(3)
进行 SVD 后,信号的大部分能量集中在较大的
奇异值中, 而较小 的奇异值 中 则更多的 是噪 声信
息
[13]
。 因此,选择较大的奇异值,即 σ
i1
作为滑动窗
SVD 的输出,在提取信号变化特征的同时降低噪声
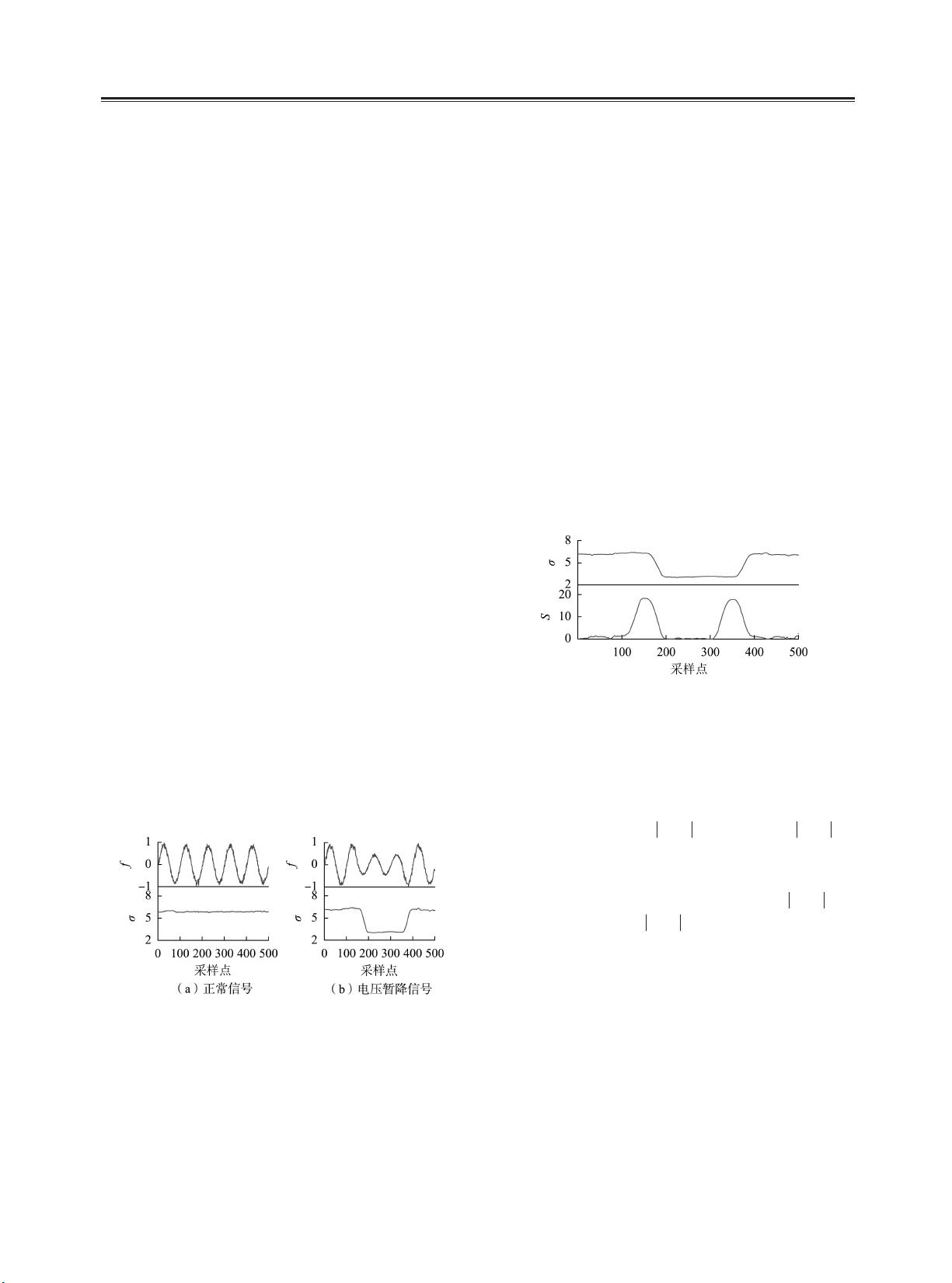
的干扰。 图 1 是信噪比 SNR( Signal⁃to⁃Noise Ratio)
为 20 dB 下正常信号及过零点处电压暂降信号经滑
动窗 SVD 输出的滑动奇异信号 σ(图中 f 为标幺值,
后同)。
图 1 信号的滑动窗 SVD 结果(SNR 为 20 dB)
Fig.1 Moving window SVD results of signals(SNR is 20 dB)
由图 1 可知,滑动奇异信号能实时反映被测信
号的波形变化,在有扰动的情况下,σ 发生梯度变化
的位置即对应暂态扰动发生 / 结束的时刻。
1.2 奇异值梯度及自适应阈值检测
结合滑动奇异信号的特点,为了突出 σ 的坡度
变化时刻,可通过后向差分方法提取信号梯度信息,
但传统的点间差分通常为前向或后向两点间差分,
虽能突出信号的异常,但定位结果不精确,且传统差
分方法的抗噪性较差,通常需结合滤波或其他特征
提取方法
[14⁃15]
。
本文中的滑动奇异信号 σ 是被测信号 f 以滑动
窗宽 T / 2 构造矩阵后经 SVD 获得,当点间间隔为
T / 2 时由差分获得的极大值指示的扰动起止时刻最
准确。 因此,本文提出半周波点间差分,通过式(4)
构造指示信号 S,获得奇异值梯度信息。
S(i)
=
abs(σ(i
+
T / 2)
-
σ(i))median(σ) (4)
其中,median(·) 为取中值函数;abs(·) 为取绝对值
函数。
通过式(4)构造的扰动指示信号的峰值可准确
定位扰动时刻,函数 median(·) 的作用是放大波峰
信号,结合自适应阈值可检测是否发生扰动,并定位
扰动指示信号的波峰,即扰动起止时刻。
图 2 为与图 1( b) 相对应的滑动奇异信号 σ 的
指示信号 S, S 的 极 大 值 即 对 应 扰 动 发 生 和 结 束
时刻。
图 2 扰动指示信号
Fig.2 Disturbance indication signal
自适应阈值是一个重要的参数,其准确性对最
终的扰动检测及定位结果的影响较大。 依据文献
[16]中的经典阈值去噪方法,通常将阈值设为如下
形式:
τ
=
c·1.482 6 median( dd
H
)
=
C·median( dd
H
)
(5)
其中,c、C 均为常数,c 可依据实际情况进行调整,以
获得最优阈值检测结果;1.482 6 median( dd
H
) 为
原信号噪声估计
[17]
, dd
H
为原信号经小波分解后
的高频子带系数。
对于进行差分后的信号,正常情况下其只包含
噪声信息,且其值不会超过阈值。 本文中,扰动指示
信号 S 的构造过程已经由选取较大的奇异值滤除部
分噪声,式(5) 所示的阈值设置方法已不能有效地
估计噪声的变化,且采用小波分解获得高频子带系
数无疑增加了计算量。 考虑式(4) 中 median(σ) 与
噪声的关系,在不同的 SNR 下 对 正 常 信 号 进 行 测
试,结果如表 1 所示。
由表 1 知,median( σ) 随着噪声强度的增大而
减小,随着噪声强度的减小而增大;则 1 / median( σ)
随着噪声强度的增大而增大,随着噪声强度的减小
剩余7页未读,继续阅读
资源评论

weixin_38650516
- 粉丝: 11
- 资源: 971
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 二维码图形检测6-YOLO(v5至v9)、COCO、CreateML、Darknet、Paligemma、TFRecord数据集合集.rar
- Matlab绘制绚丽烟花动画迎新年
- 厚壁圆筒弹性应力计算,过盈干涉量计算
- 网络实践11111111111111
- GO编写图片上传代码.txt
- LabVIEW采集摄像头数据,实现图像数据存储和浏览
- 几种不同方式生成音乐的 Python 源码示例.txt
- python红包打开后出现烟花代码.txt
- 嵌入式 imx6 linux gdb工具
- 乒乓球检测22-YOLO(v5至v11)、COCO、CreateML、Paligemma、TFRecord、VOC数据集合集.rar
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功