IEEE COMMUNICATIONS LETTERS, VOL. 19, NO. 5, MAY 2015 831
Modeling and Analysis of Coverage in 3-D Cellular Networks
Ziyu Pan and Qi Zhu
Abstract—Cellular networks are usually modeled by the point
process theory and stochastic geometry with mobile users either
scattered randomly or deterministically set. These models are
used widely in a 2-D space but are not suitable for dense urban
environment in which a large number of small cells are distributed
to satisfy the rapid increase in mobile subscribers as well as the
traffic demand. In this paper, a new general model based on a
3-D space for a cellular network is proposed. Under general as-
sumptions, the coverage probability of downlink cellular networks
can be obtained by fast integral calculation and in some special
cases can be simplified to an analytical form. Compared with the
2-D space model and actual small cells deployment, the proposed
3-D space model is more accurate and provides a closer bound
of coverage probability. In addition to being more tractable, the
model proposed in this paper can better capture the increasingly
opportunistic and dense small cells deployment in future hetero-
geneous cellular networks.
Index Terms—3-D cellular networks, coverage probability,
signal-to-interference-plus-noise ratio (SINR), stochastic
geometry.
I. INTRODUCTION
W
ITH the rapid increase in mobile users and growing ur-
banization, cellular networks have experienced several
major evolutions, from the first generation to the present LTE-
based 4G cellular networks [1]. To meet the demands of all
types of customers and reduce network costs, a micro base
station (BS) concept has been proposed, such as the femtocell
and picocell [2]. In this case, how to model the increasing
heterogeneous cellular networks becomes an important issue.
A tractable model-based information theory is the Wyner
model [3]–[5], which is overly simple and typically one-
dimensional. For cellular systems such as LTE-based 4G, the
Wyner model and related mean-value approaches are inaccurate
because of the dramatic variation in the SINR value.
On the other hand, a 2-D network model of BSs on a random
station was proposed in [6]. In that study, the locations of the
BSs were modeled as a homogeneous Poisson point process
(PPP) with density λ, instead of assuming they were placed
on a regular grid. Furthermore, a multi-tier cellular network
where all network tiers were assumed to follow independent
homogenous PPPs and all tiers used the same frequency chan-
nel was modeled in [7], and high diversity of cell loads in a
K-tier cellular network was analyzed in [8]. In [9], this 2-D
network model was adopted to analyze the optimal BS density
Manuscript received December 7, 2014; accepted February 26, 2015.
Date of publication March 11, 2015; date of current version May 7, 2015.
This work is supported by National Basic Research Program of China
(973 program: 2013CB329005), National Natural Science Foundation of China
(61171094, 61401225), and Jiangsu Provincial National Science Foundation
(BK20140894). The associate editor coordinating the review of this paper and
approving it for publication was G. Giambene.
The authors are with the Key Wireless Laboratory of Jiangsu Province,
School of Telecommunication and Information Engineering, Nanjing Uni-
versity of Posts and Telecommunications, Nanjing 210003, China (e-mail:
panziyu@njit.edu.cn; zhuqi@njupt.edu.cn).
Digital Object Identifier 10.1109/LCOMM.2015.2411599
Fig. 1. Poisson-distributed small cells and a target user.
for both homogeneous and heterogeneous cellular networks
with service outage probability constraint. Different from the
aforementioned downlink analysis, a model for cellular uplink
analysis and simple expression for coverage probability were
presented in [10]. These abovementioned papers are all based
on a 2-D network model.
The abovementioned 2-D model is very tractable for macro
BSs in rural or suburban environment, but is not suitable for a
dense urban area, especially the small cells in high-rise centers.
In this case, a general 2-D model cannot accurately describe
the system characteristics (especially the distance between a
user and the BS); thus, we need a more elaborate 3-D model.
In this study, we extend the traditional 2-D model to a 3-D to
obtain the coverage probability of a cellular network in high-
rise centers (small cells such as femtocells). We focus on the
3-D model and provide simple and tractable coverage prob-
ability of a target user. Compared with the 2-D model and
actual small cells deployment, the proposed 3-D model is more
accurate in a high-rise center environment and can provide a
closer bound of coverage probability.
II. D
OW N L I N K SYSTEM MODEL
The cellular network model consists of small cells arranged
according to homogeneous PPP Φ with intensity λ in a
3-D space. Let us consider an independent collection of mo-
bile users, which are located according to some independent
stationary point processes. We assume that each mobile user
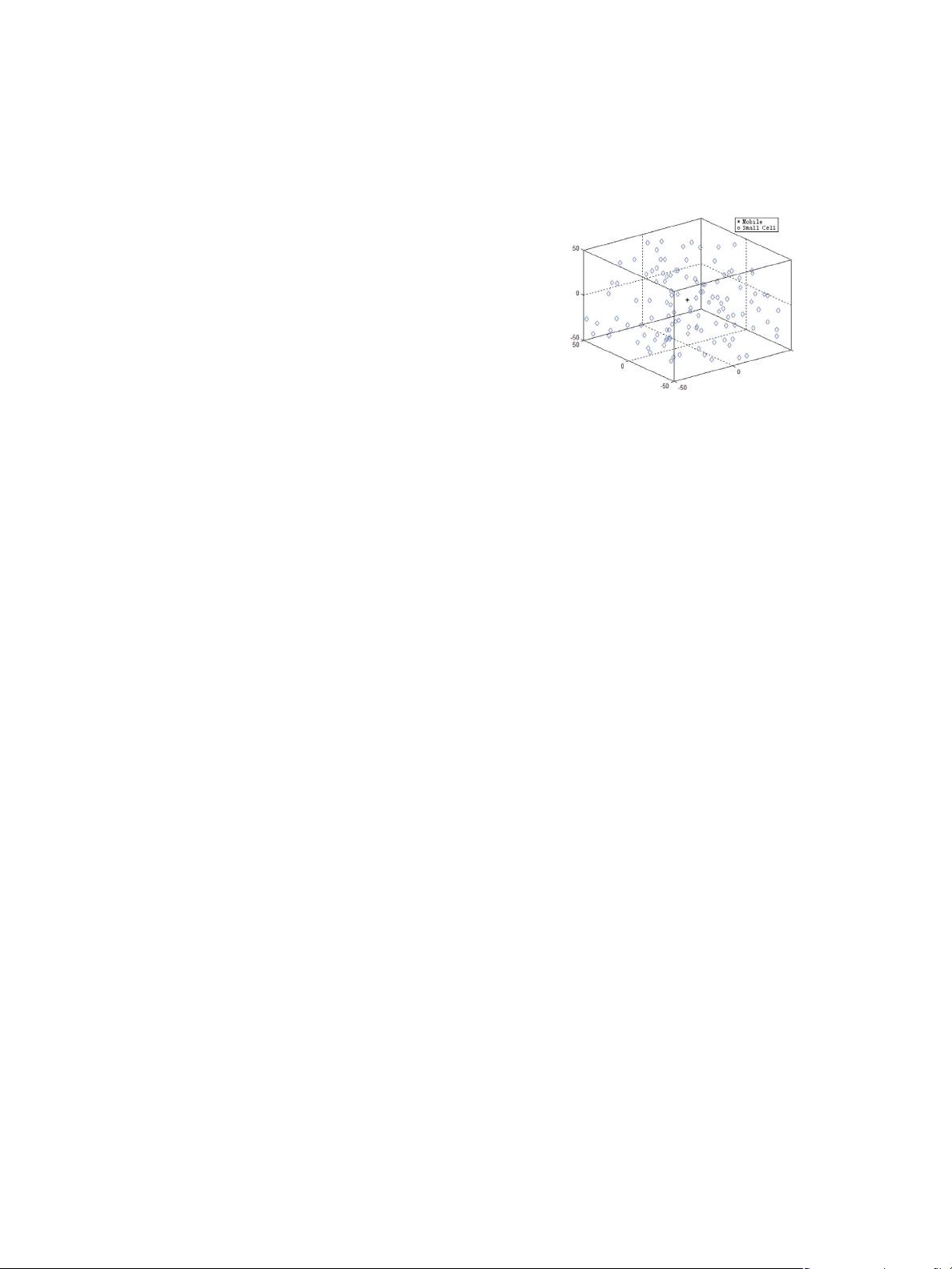
communicates with the nearest small cell, as shown in Fig. 1.
We have also obtained the coordinates of an actual small cell
deployment by mobile operators. This deployment stretches
approximately 0.3 km
2
in Xinjiekou area in Nanjing, China,
where a large number of high buildings are located. We show
the middle 100 × 100 × 100 m in Fig. 2 where 150 small
cells are deployed. These small cells are installed by different
persons; thus, their positions are all independent from one
another. This independence is identical to the characteristics of
a 3-D PPP (the spatial distribution of the points is independent).
In this case, we assume that the small cells can be modeled as
a homogeneous PPP. The standard power loss model is used
with path loss exponent α>2. Considering a high-rise center
environment, we use the floor attenuation factor (FAF) path loss
1558-2558 © 2015
IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功
评论0