Energy-Based Controller Decoupling of Powered
Parafoil Unmanned Aerial Vehicle
Li Bingbing
1, 2
, Yang Liying
1
, He Yuqing
1
, Han Jianda
1
1 State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016,
China
2 University of Chinese Academy of Sciences, Beijing 100049, China
Abstract—Powered Parafoil Unmanned Aerial Vehicle
(PPUAV), which is suitable for large-area and long-time
surveillance and airdrop missions, is a type of innovative
UAV. It consists of parafoil canopy, payload and suspension
lines, and has the advantages of simple structure, low cost
and high load capacity. However, due to the apparent mass
and flexible connection, it is hard to build an accurate
model for controller design for PPUAV. Normal PID
controller is unsuitable for PPUAV because of the inputs'
coupling effects on outputs. This paper presents an
applicable method of modeling to capture the main
characteristics of PPUAV, and the proposed model is
validated by actual flight test. To deal with the coupling
effect, a novel control method based on energy is proposed.
The method has clear adjustment procedures and is more
practical and effective than normal PID controller. The
simulation results show its effectiveness on PPUAV.
Keywords—powered parafoil; UAV; model simplification;
system identification; input and output coupled system;
energy-based controller; controller decoupling
I. INTRODUCTION
A. Introduction of PPUAV
Powered Parafoil Unmanned Aerial Vehicle (PPUAV)
is a small aircraft, which is able to cover large horizontal
distances from the release point. It provides a unique
capability for air-transport of heave payloads according
to the high payload-weight-ratio[1]. PPUAV is compact
before parafoil deployment and lightweight, and it flies at
low speed and impacts the ground with low velocity.
PPUAV is often considered to be safer than normal
fixed-wing aircraft because of its inherent stability,
limited response to control inputs, and stall resistance[2].
All of the above advantages make it a suitable platform
for field investigations, search and rescue, and
delivery[3].
However, PPUAV has the characteristics of
complexity, uncertainty, nonlinearity, time-varying,
control delay and large inertia, and is easily affected by
the atmospheric environment[4]. PPUAV is strongly
influenced by apparent mass because of its light
weight[5]. A unique feature of PPUAV is the high degree
of variability of flight dynamic, which make its practical
applications to be a great challenge[6].
B. Control mechanism
The general control mechanism for PPUAV is left
and right brake deflection and thrust provided by the
engine. The asymmetric deflection of left or right brake
makes PPUAV to turn. And the engine provides thrust to
take off and accelerate. Predictable changes in
aerodynamic loads is caused by thrust and canopy
changes, which is the method of controlling PPUAV. The
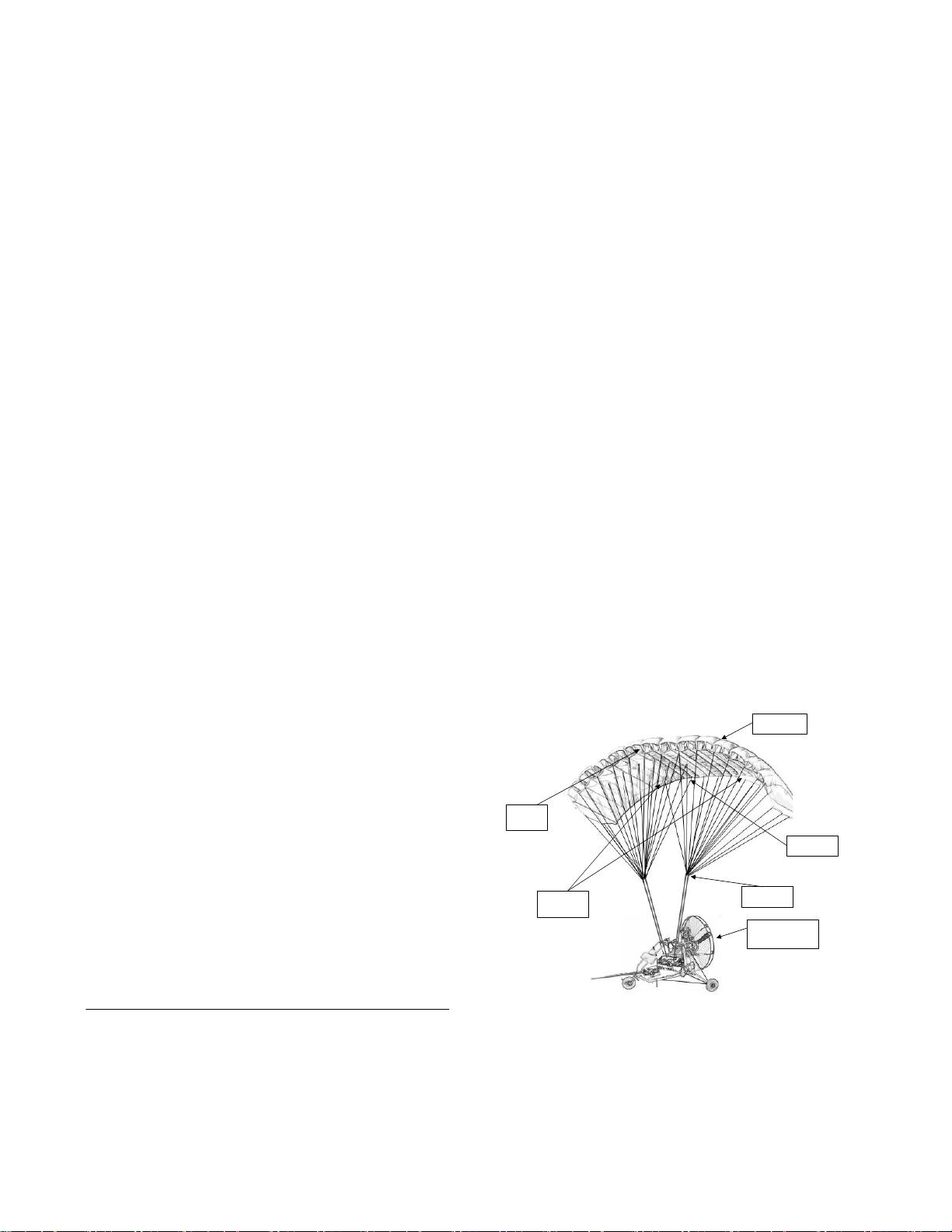
structure of the system is shown in Fig. 1.
Parafoil
Canopy
Leading
Edge
Control
Ropes
Unmanned
Powered Vehicle
Suspension
Ropes
Trailing
Edge
This work is supported by National Nature Sciences Foundation of
China(Grant No. 61503369 and 61528303) / The state key laboratory of
robotics / Chinese National Key Technology R&D Program （Grant No.
Y4A1208101）
剩余7页未读，继续阅读
资源评论
