单片机与DSP中的有源滤波器的低通和高通响应

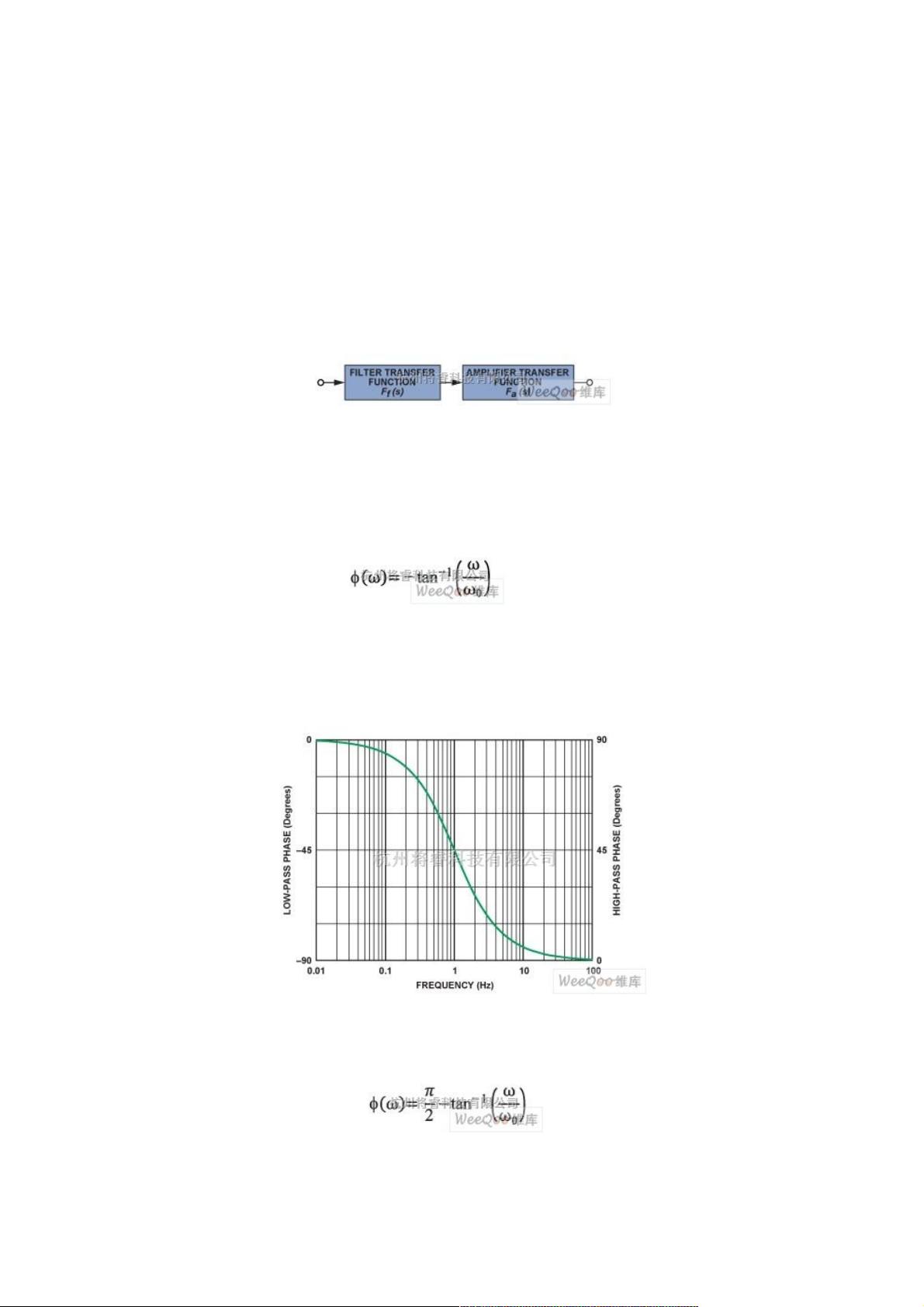
上一篇文章1 讨论了滤波器相位与滤波器实现拓扑之间的关系，本篇将讨论滤波器传递函数本身的相位漂移。虽然滤波器主要是针对幅度响应而设计的，但在延时仿真、级联滤波器电路特别是过程控制环路等应用中相位响应非常重要。 　　本文主要讨论低通和高通响应。后续系列文章还将讨论带通和陷波(带阻)响应、全通响应以及滤波器的脉冲与阶跃响应。 　　回顾以前的文章可知，有源滤波器的传递函数可以被看作是滤波器传递函数和放大器传递函数的级联响应(图1)。 图1. 以两个级联的传递函数的形式表示的滤波器。 　　低通传递公式 　　首先，我们再看一下传递公式的相位响应。 　　对于单极点低通滤波器，传递函数的相移 在电子工程领域，有源滤波器是一种广泛应用的器件，特别是在单片机和数字信号处理器(DSP)系统中。有源滤波器能够通过调整电路参数来改变信号的幅度和相位特性，以达到筛选特定频率成分的目的。本文将重点讨论有源滤波器中的低通和高通响应，这是理解滤波器工作原理的关键部分。 滤波器的设计通常基于其传递函数，该函数描述了输入信号如何被转换为输出信号。在有源滤波器中，传递函数由滤波器本身的特性以及与其连接的放大器的传递函数共同决定。如图1所示，滤波器的传递函数可以视为两者的级联响应。 低通滤波器允许低频信号通过，同时衰减高频信号。对于单极点低通滤波器，其相位响应可由公式(1)给出，相移随着频率的增加而线性增加，直到90°。在中心频率ω0处，相移为-45°。例如，图2的左轴展示了这种相位响应，频率从中心频率的20倍频下降低到20倍频以上。 高通滤波器则相反，它允许高频信号通过，衰减低频信号。单极点高通滤波器的相位响应如公式(2)所示，在中心频率ω0处相移为+45°。图2的右轴描绘了这种相位响应。 低通滤波器的输出相对于输入滞后，而高通滤波器的输出则领先。这种相位差在图3中通过比较输入和不同滤波器输出的波形得到直观展示。当输入信号为1kHz正弦波时，高通滤波器的输出领先45°，低通滤波器的输出滞后45°。 对于更复杂的滤波器，如二阶滤波器，其相位响应更加复杂。双极点低通滤波器的相位响应可以近似为公式(3)，而双极点高通滤波器的相位响应接近公式(4)。这两个公式考虑了阻尼比α，它影响幅度响应的峰值和相位变化的陡峭程度。 在实际应用中，即使是高通滤波器也会受到放大器自身低通特性的影响，这意味着高通滤波器实际上也是一个带通滤波器。图5展示了双极点低通滤波器的相位和增益响应随Q值变化的情况，Q值影响相位变化的范围和幅度响应的形状。 总结来说，理解有源滤波器的低通和高通响应是设计和分析滤波器系统的基础。相位响应在系统延时、级联滤波器设计和过程控制等应用中至关重要。通过调整滤波器的参数，我们可以精确地塑造信号的频率特性，实现信号处理的各种需求。无论是单极点还是双极点滤波器，其相位响应都直接影响着信号的传输质量，为系统性能提供了关键的优化手段。