没有合适的资源?快使用搜索试试~ 我知道了~
On the solution of Dirichlet’s problem of complex Monge-Amp`ere ...
0 下载量 47 浏览量
2019-12-30
04:13:52
上传
评论
收藏 318KB PDF 举报
温馨提示
第二类Cartan-Hartogs域上复Monge-Amp`ere 方程 Dirichlet 问题的解 ,殷慰萍,殷晓岚,Complex Monge-Amp`ere equation is a nonlinear equation with high degree, therefore to get its solution is very difficult. In present paper how to get the solution of Dirichlet’
资源推荐
资源详情
资源评论

On the solution of Dirichlet’s problem of
complex Monge-Amp`ere equation on
Cartan-Hartogs domain of the second type*
1
Weiping YIN
1
Xiaolan YIN
2,3
1. School of Mathematical Sciences, Capital Normal University, Beijing
100037, China. e-mail: wyin@mail.cnu.edu.cn Tel: 86-10-68902600
2. Technology Center of Software Engineering, Institute of Software, Chinese
Academy of Sciences, Beijing 100080, China.
3. Graduate University of Chinese Academy of Sciences, Beijing 100049,
China.
Abstract: Complex Monge-Amp`ere equation is a nonlinear equation with
high degree, therefore to get its solution is very difficult. In present paper how
to get the solution of Dirichlet’s problem of Complex Monge-Amp`ere equation
on the Cartan-Hartogs domain of the second type is discussed by using the
analytic method. Firstly, the complex Monge-Amp`ere equation is reduced to
the nonlinear ordinary differential equation, then the solution of the Dirichlet’s
problem of complex Monge-Amp`ere equation is reduced to the solution of two
point boundary value problem of the nonlinear second-order ordinary differ-
ential equation. Secondly, the solution of the Dirichlet’s problem is given in
semi-explicit formula, and under the special case the exact solution is obtained.
These results may be helpful for the numerical method of Dirichlet’s problem
of complex Monge-Amp`ere equation on the Cartan-Hartogs domain.
Key Words Complex Monge-Amp`ere equation, Dirichlet’s problem,
Cartan-Hartogs domain, Kaehler-Einstein metric.
MR(1991)Subject Classification: 65E05, 32C17, 53C55, 35G30.
1
*This project was supported by the National Natural Science Foundation of China(Grant
No.10771144).
1
http://www.paper.edu.cn

1 Introduction
The Monge-Amp`ere equations are in general very hard to solve, but have been
used in many areas such as deferential geometry, variational method, optimiza-
tion, transfers problem and so on. Based on the existence of the solution of
certain type of complex Monge-Amp`ere equation, S.Y.Cheng, N.M. Mok, S.T.
Yau proved([1,2]) that there exists unique complete Kaehler-Einstein metric on
any bounded pseudoconvex domain D in C
n
. If this Kaehler-Einstein metric is
given by
ds
2
=
X
∂
2
g
∂z
i
∂z
j
dz
i
dz
j
,
actually they proved that the following Dirichlet’s problem of the complex
Monge-Amp`ere equation
det
∂
2
g
∂z
i
∂z
j
= e
(n+1)g
z ∈ D
g = ∞ z ∈ ∂D
exists unique solution. But they have not got the solution in explicit formula. In
present pape r the authors try to get the explicit solution of Dirichlet’s problem
of complex Monge-Amp`ere equation on Cartan-Hartogs domain of the s ec ond
type, which is defined as follows:
Y
II
= Y
II
(N
2
, p; K) := {W ∈ C
N
2
, Z ∈ R
II
(p) : |W |
2K
< det(I−ZZ
t
), K > 0},
where R
II
(p) is the classical domain of the second type, that is
R
II
(p) = {Z ∈ C
p(p+1)
2
: I − Z
Z
t
> 0},
where Z is symmetric matrix with p order, Z > 0 means that Z is the positive
definite matrix,
Z denotes the conjugate of Z, Z
t
indicates the transpose of Z,
2
http://www.paper.edu.cn
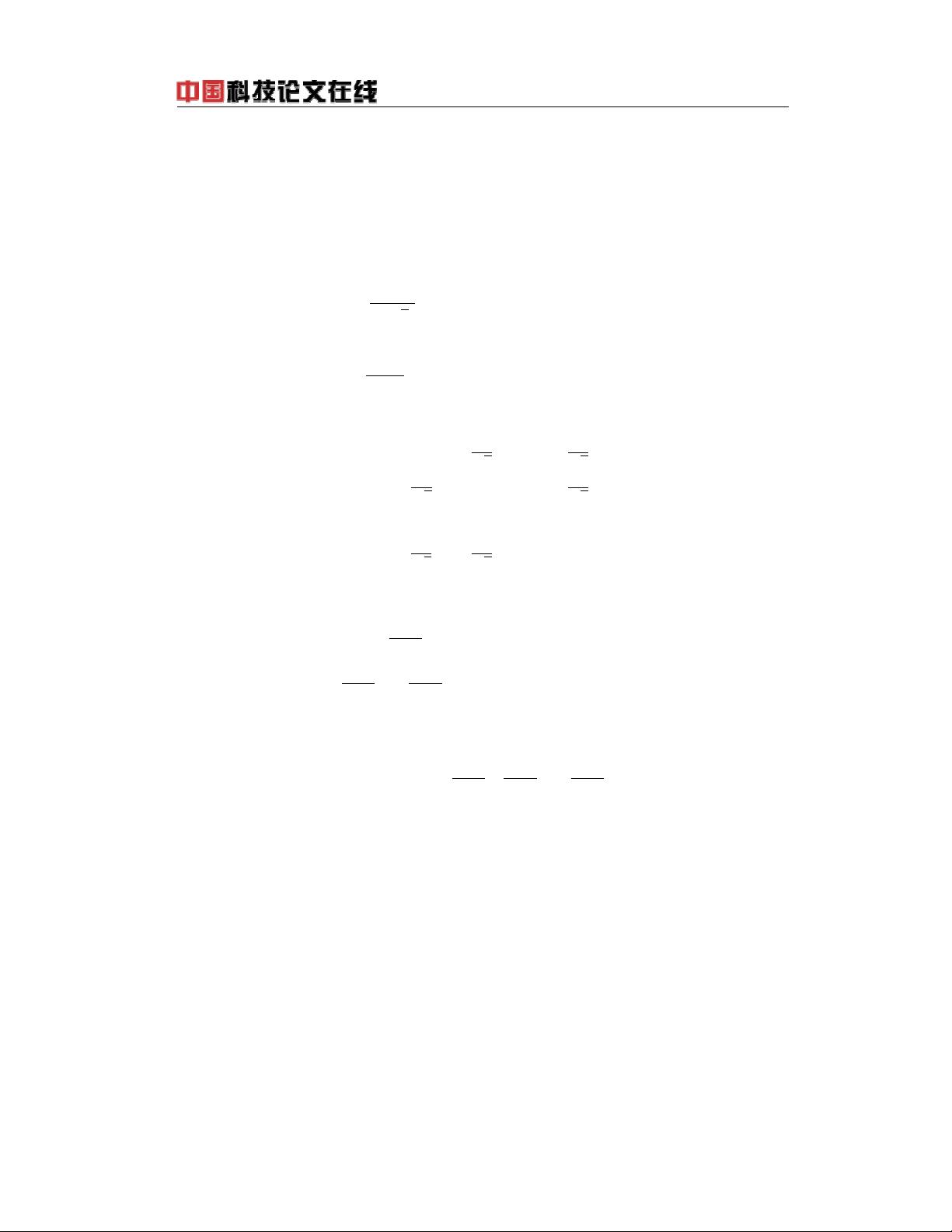
det is the abbreviation of determinant. In fact the explicit solution of follow-
ing Dirichlet’s problem of complex Monge-Amp`ere equation is discussed in this
paper:
det
∂
2
g
∂z
i
∂z
j
1≤i,j≤N
= e
(N+1)g
z ∈ Y
II
,
g = ∞ z ∈ ∂Y
II
,
(1)
where N = N
2
+
p(p+1)
2
is the complex dimension of Y
II
, and suppose
(Z, W ) ∈ Y
II
, W = (w
1
, w
2
, . . . , w
N
2
),
Z = Z
t
=
z
11
1
√
2
z
12
···
1
√
2
z
1p
1
√
2
z
21
z
22
···
1
√
2
z
2p
.
.
.
.
.
.
.
.
.
.
.
.
1
√
2
z
p1
1
√
2
z
p2
··· z
pp
let
Z
1
= (z
1
, z
2
, . . . , z
p(p+1)
2
) = (z
11
, . . . , z
1p
, z
22
, . . . , z
2p
, . . . , z
p,p
),
Z
2
= (z
p(p+1)
2
+1
, z
p(p+1)
2
+2
, . . . , z
N
) = (w
1
, w
2
, . . . , w
N
2
),
then the point (Z, W ) can b e denoted by a vector z with N entries, that is
z = (Z
1
, Z
2
) = (z
1
, z
2
, . . . , z
p(p+1)
2
, z
p(p+1)
2
+1
, z
p(p+1)
2
+2
, . . . , z
N
).
Due to its explicit formula the Bergman kernel function of Y
II
is Bergman
exhaustion[3], hence the domain Y
II
is the pseudoconvex domain. Therefore
the solution of problem (1) is existent and unique. In general domain Y
II
is the
nonhomogeneours domain.
In present paper the authors prove that the solution of problem (1) can be
got in semi-explicit formula, and under the special case the explicit solution is
also obtained. The main result of present paper can be stated as follows:
3
http://www.paper.edu.cn
剩余13页未读,继续阅读
资源评论

weixin_38623919
- 粉丝: 6
- 资源: 929
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 【创新无忧】基于鲸鱼优化算法WOA优化广义神经网络GRNN实现光伏预测附matlab代码.rar
- 【创新无忧】基于鲸鱼优化算法WOA优化广义神经网络GRNN实现数据回归预测附matlab代码.rar
- 【创新无忧】基于鲸鱼优化算法WOA优化相关向量机RVM实现北半球光伏数据预测附matlab代码.rar
- 【创新无忧】基于鲸鱼优化算法WOA优化极限学习机ELM实现乳腺肿瘤诊断附matlab代码.rar
- 【创新无忧】基于鲸鱼优化算法WOA优化极限学习机KELM实现故障诊断附matlab代码.rar
- 【创新无忧】基于鲸鱼优化算法WOA优化相关向量机RVM实现数据多输入单输出回归预测附matlab代码.rar
- 小戴人工智能PurposeAI-20241205分词字符集识别的程序的详细解释 (第四版)
- 开始使用BigQuery访问HTTP Archive.pdf
- Web网页设计期末大作业 (模拟故宫博物馆).zip
- 基于node运行的JavaScript文件
- 【创新无忧】基于开普勒优化算法KOA优化广义神经网络GRNN实现电机故障诊断附matlab代码.rar
- 【创新无忧】基于开普勒优化算法KOA优化广义神经网络GRNN实现光伏预测附matlab代码.rar
- 【创新无忧】基于开普勒优化算法KOA优化广义神经网络GRNN实现数据回归预测附matlab代码.rar
- 【创新无忧】基于开普勒优化算法KOA优化相关向量机RVM实现北半球光伏数据预测附matlab代码.rar
- 【创新无忧】基于开普勒优化算法KOA优化极限学习机KELM实现故障诊断附matlab代码.rar
- 【创新无忧】基于开普勒优化算法KOA优化极限学习机ELM实现乳腺肿瘤诊断附matlab代码.rar
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功