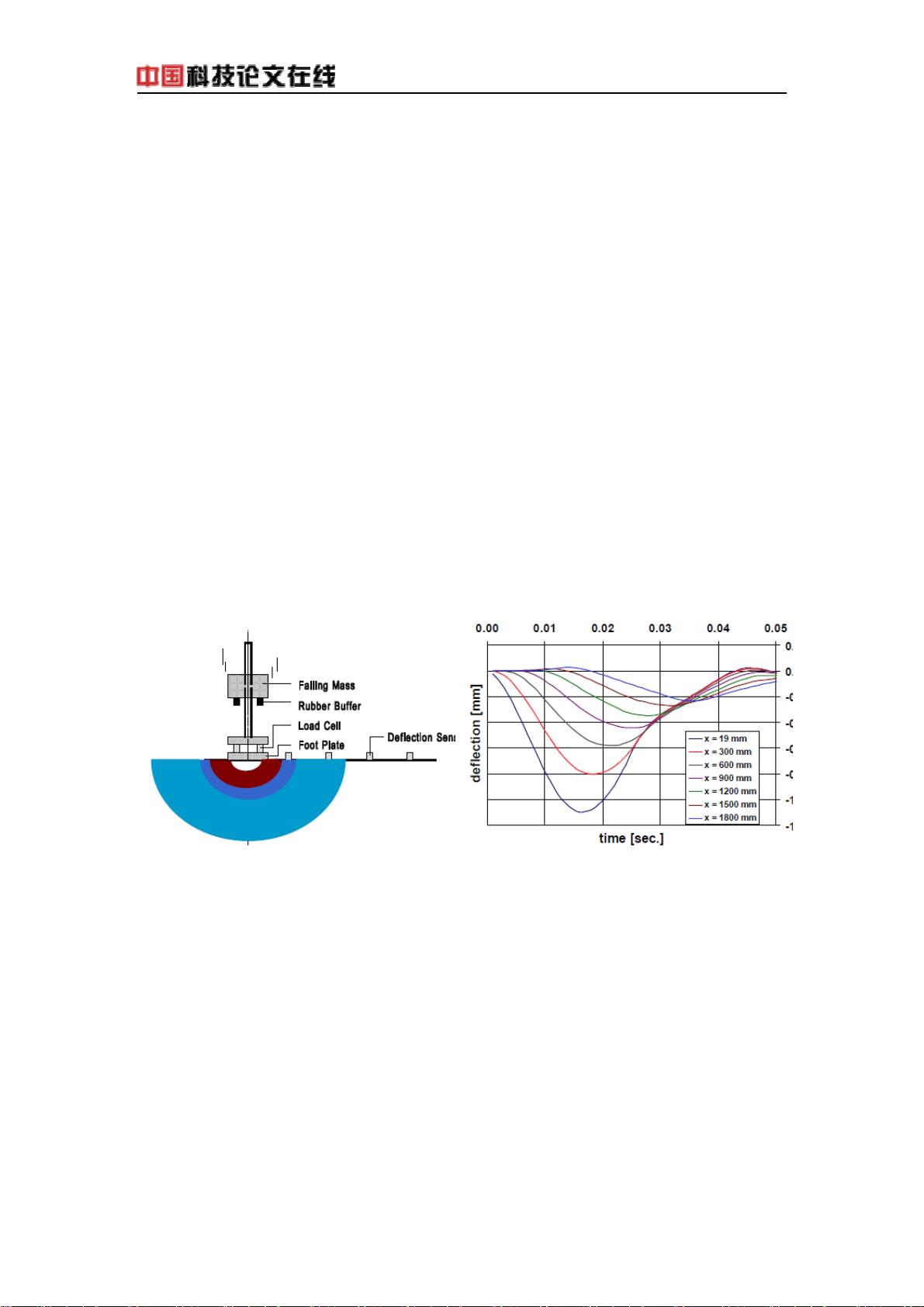
路面动态弯沉计算是道路工程中用于评价路面结构承载能力的重要技术手段,其计算准确性直接影响到道路维护和修补策略的制定。传统的计算方法多基于静态算法,但这些算法无法充分反映FWD(落锤式弯沉仪)检测过程中的动态特性,因此在精度上存在一定的偏差。谱元法作为一种结合波动方程和有限元原理的数值计算方法,能够更准确地模拟FWD检测中的动态过程,从而提高了计算精度。本文主要探讨谱元法在路面动态弯沉计算中的应用,通过结合波动方程和有限元原理,利用傅立叶变换和贝塞尔级数,实现了时间-频率、空间-波数的互换,提出了动态路面弯沉的快速算法,并通过实例验证了算法的正确性。 道路工程中的弯沉测试通常使用FWD设备来完成。FWD设备通过施加冲击荷载到路面上,模拟车辆对道路的动态荷载作用。这种荷载在路表产生应力波,并以半球状向路面结构内部传播,造成路表振动,进而引起路面的弯沉。检测所得的数据将用于反算路面结构层模量,而这一反算过程的准确性对于道路养护策略的制定至关重要。 传统的FWD反算方法大多基于静态算法,即通过静态平衡方程来反算结构层的模量。然而,这种算法忽略了FWD检测过程中的动态特性,从而导致计算结果与实际存在偏差。为了更准确地描述FWD检测的动态过程,需要采用能够反映动态特性的分析方法。R.Al-Khoury提出的FWD分析方法的三个要素包括:能够反映检测的动态过程、考虑不同荷载形式的脉冲特性、实用性强,可以满足工程需求。 在解决动态问题上,常用的两种方法是解析法和数值方法。解析法能提供波动方程的精确解,但其适用范围受限于特定的求解域和边界条件。而对于复杂的路面结构和荷载情况,解析法往往无法适用。数值方法,特别是有限元方法,虽然能够处理复杂的几何形状和边界条件,但在处理动态问题时,计算量大且计算时间长,影响了其在FWD反算中的应用。 谱元法是一种新的数值计算方法,结合了波动方程的精确性和有限元方法的灵活性。谱元法通过在有限的频域和波数上进行双重求和,避免了在无穷区域上计算数值积分的不便。与传统方法相比,谱元法能够利用较少的计算元素精确描述结构的动态响应,极大地提高了运算速度,使得在FWD反算中的应用成为可能。本文通过谱元法的应用,提出了一种路面结构的FWD动态计算方法,能够更准确地模拟路面弯沉盆的变化,并通过计算实例验证了该方法的有效性。 在实现谱元法的过程中,需要引入结构刚度矩阵来求解结构在荷载作用下的位移响应。刚度矩阵的形式与传统刚度矩阵类似,但有所不同的是求解域为频率-波数域,且刚度矩阵、位移向量及力向量均为复数。通过叠加单层刚度矩阵,可得到层状体的总刚矩阵,其叠加方法与有限元方法相同。单层刚度矩阵的参数包括剪切模量、膨胀波波速、畸变波波速和层厚等。 通过谱元法开发的计算程序DDC,能够计算出路面结构在不同冲击时间下的弯沉响应,并将计算结果与BISAR3.0软件包的计算结果进行比较。研究表明,路面弯沉与荷载作用时间关系密切,作用时间越长,弯沉值和弯沉盆的斜率越大。当作用时间足够长时,整个过程趋近于准静态过程,此时的计算结果与BISAR3.0的结果近似相同,从而验证了谱元法计算的正确性。通过这一方法,可以更精确地掌握路面结构的动态弯沉特性,为道路工程的设计、施工和维护提供更科学的依据。
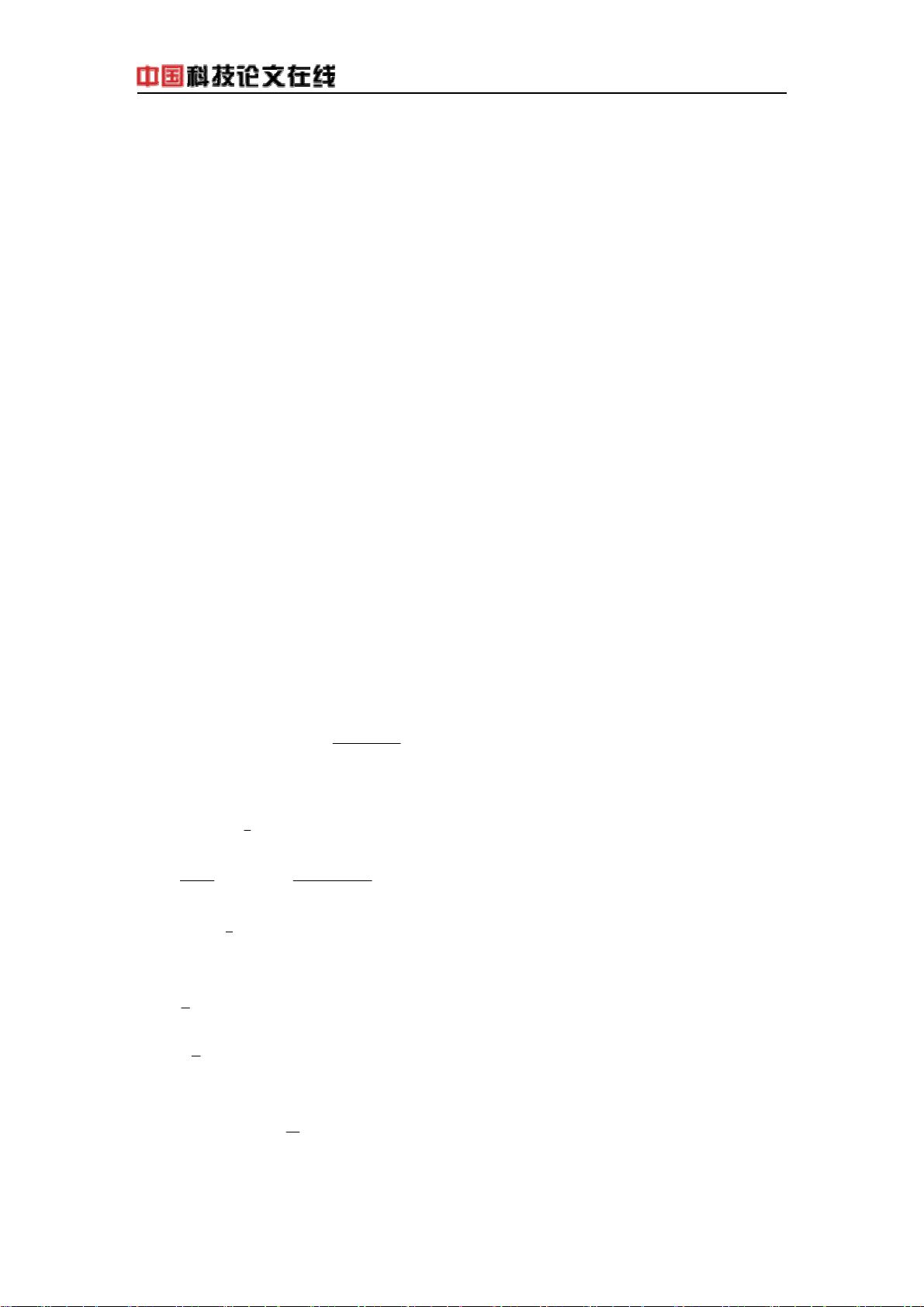
剩余6页未读,继续阅读

- 粉丝: 3
- 资源: 933
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功