水平通道内黏性指进现象LBM模拟(2012年)

自然科学

论文

需积分: 19 36 浏览量 2021-06-17 17:53:44 上传评论收藏 1.88MB PDF 举报

资源推荐

资源详情

资源评论

第５２卷第３期

２０１２年５月

大连理工大学学报

ＪｏｕｒｎａｌｏｆＤａｌｉａｎＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙ

Ｖｏｌ．５２，Ｎｏ．３

Ｍａｙ２０１２

文章编号：１０００‐８６０８（２０１２）０３‐０３４３‐０７

水平通道内黏性指进现象ＬＢＭ模拟

李维仲

倡

，　董　波，　宋永臣

（大连理工大学海洋能源利用与节能教育部重点实验室，辽宁大连　１１６０２４）

摘要：

采用格子Ｂｏｌｔｚｍａｎｎ方法（ＬＢＭ）研究了水平通道内非混相驱替过程中的黏性指进现

象．考察流动方向与重力方向垂直时，驱替和被驱替流体间黏度比及壁面可润湿性的影响，比

较了不同条件下的指进前缘形状，并利用突破时间和面积扫掠效率分析了驱替效率．研究表

明，在重力的影响下，指进前缘形状关于水平通道的中心线是非对称的．随着非混相流体间黏

度比的增大，指进现象也随之增强，导致驱替效率降低．当驱替流体不易润湿通道壁面时，指

进现象被强化；当驱替流体易于润湿通道壁面时，指进现象则被抑制．

关键词：黏性指进；非混相流体；表面可润湿性；黏度比

中图分类号：ＴＥ３１９文献标志码：Ａ

收稿日期：２０１０‐１０‐１１；　修回日期：２０１２‐０３‐２５．

基金项目：国家自然科学基金资助项目（５０９７６０１７；５０７３６００１）．

作者简介：李维仲

倡

（１９５６‐），男，教授，博士生导师，Ｅ‐ｍａｉｌ：ｗｚｈｏｎｇｌｉ＠ｄｌｕｔ．ｅｄｕ．ｃｎ．

０　引　言

黏性指进现象广泛存在于油气开采过程中，

是多相渗流的重要特征之一．指进现象的出现会

导致驱替流体的过早突破，使得波及体积减小，原

油采收率降低，因此研究者对这一现象进行了大

量的研究．线性稳定性分析方法被广泛用来分析

毛细扩散、黏度比以及岩石可润湿性对指进现象

的影响，但至今，还没有一套基于连续介质假设的

相对成熟的理论来描述指进现象的演化过程和定

量地刻画其形态特征

［１、２］

．此外基于分形理论的

扩散限制凝聚模型

［３］

也被用来模拟多孔介质内非

混相驱替过程中的指进现象，虽然取得了一定进

展，但是还需进一步探讨分形理论的物理意义与

黏性指进的物理机制的内在联系

［４］

．

格子Ｂｏｌｔｚｍａｎｎ方法（ＬＢＭ）是一种介于微

观的流体分子动力学模型和宏观的连续介质模型

的介观方法．该方法算法简单，易于程序化处理，

具有良好的并行特性，近十几年来发展非常快．

ＬＢＭ已经被广泛地应用于多相多组分流体系统

及工程传热传质问题等多个领域，包括黏性指进

等复杂现象．Ｃｈｉｎ等

［５］

研究了二维通道内的两组

分流体驱替问题，分析了不同黏度比对驱替过程

的影响．Ｇｒｏｓｆｉｌｓ等

［６］

通过分析密度等值线讨论

了Ｈｅｌｅ‐Ｓｈａｗ槽的指进不稳定性问题．Ｋａｎｇ

等

［７］

考察了二维通道内黏度比、毛细管数、表面可

润湿性对指进现象的影响．Ｈｕａｎｇ等

［８］

研究了二

维多孔介质内的驱替过程中，黏性比以及壁面可

润湿性对黏性耦合问题的影响．Ｂｏｅｋ

［９］

模拟了二

维通道内的黏性指进现象，以及多孔介质内的两

相驱替问题．这些研究讨论了黏度比的影响，但是

大多忽略了重力作用．Ｃｈａｕ等

［１０］

考察了二维多

孔介质内排驱过程中，流体流动方向和重力方向

相同时的情况．然而，流体流动方向与重力方向垂

直情况下的研究尚未见报道．本文着重讨论水平

通道内非混相驱替过程中黏性指进现象，考察当

流动方向与重力方向垂直时，黏性比以及壁面可

润湿性对指进形成、前缘形状以及驱替效率的影

响．

１　ＬＢＭ简介

本文采用Ｓｈａｎ和Ｃｈｅｎ于１９９３年

［１１］

提出的

多组分模型（伪势模型）来进行两相流体的驱替过

程模拟．该模型中，对于模拟非混相流体系统而

言，流体间界面可以自动形成，而不需要像传统方

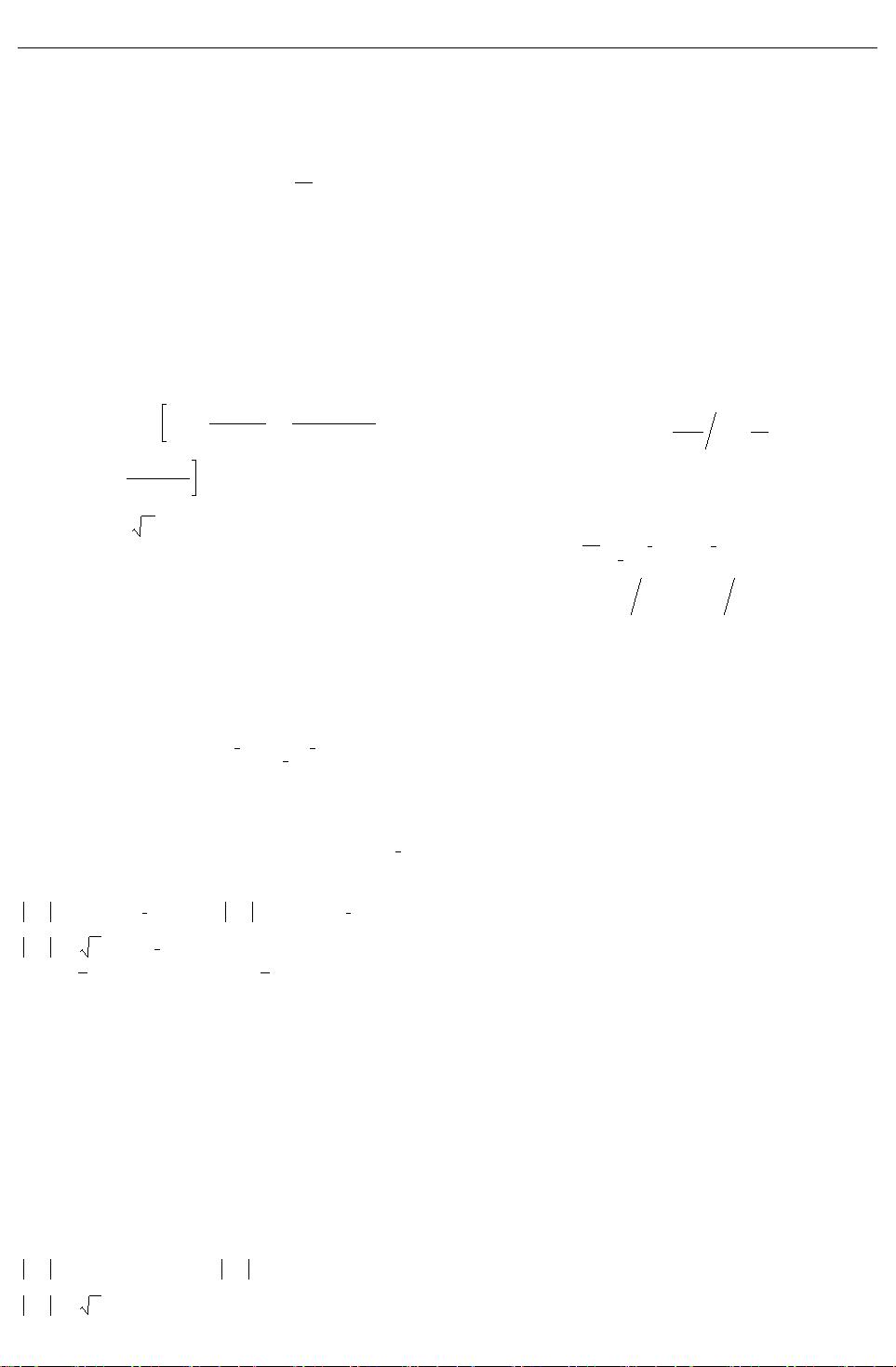
法那样进行复杂的界面重构或者界面捕捉．不同

的流体组分采用不同的流体粒子分布函数，每类

流体的粒子分布函数的演化方程为

ｆ

（ｘ

＋

ｅ

ｔ

，ｔ

＋

ｔ

）＝

ｆ

（ｘ，ｔ）－

１

［

ｆ

（ｘ，ｔ）－

ｆ

（ｅｑ）

（ｘ，ｔ）］（１）

式中：

ｆ

（ｘ，ｔ）是第

类流体在ｔ时刻、ｘ处的粒子

分布函数，

ｆ

（ｅｑ）

（ｘ，ｔ）为第

类流体对应的平衡态

粒子分布函数；

是第

类流体的松弛时间；ｅ

是

粒子离散速度向量，

为离散速度方向．

每类流体粒子的平衡态粒子分布函数为

ｆ

（ｅｑ）

＝

ｗ

１

＋

ｅ

ｕ

ｅｑ

ｃ

２

ｓ

＋

（ｅ

ｕ

ｅｑ

）

２

２ｃ

４

ｓ

－

ｕ

ｅｑ

ｕ

ｅｑ

２ｃ

２

ｓ

（２）

式中：ｃ

ｓ

＝

ｃ／３，是格子声速．ｗ

为权系数，对于

Ｄ２Ｑ９模型，当

＝

０时，ｗ

＝

４／９；当

＝

１

～

４

时，ｗ

＝

１／９；当

＝

５

～

８时，ｗ

＝

１／３６．

该模型中，假设流体粒子之间存在非局部的

相互作用势，如果只考虑邻近和次邻近粒子之间

的相互作用力，第

类流体粒子受到的作用力

Ｆ

ｆ

（ｘ）可表示为

［１２］

Ｆ

ｆ

（ｘ）＝－

（ｘ）Ｇ

σσ

∑

ｘ

′

∑

（ｘ

′

）ｅ

（３）

式中：ｘ

′

＝

ｘ

＋

ｅ

，为ｘ位置在第

方向上的邻近点

位置；而

（ｘ）称为第

组分的“有效密度” ，是局

部密度的函数，这里采用

（ｘ）＝

．参数Ｇ

σσ

用

来控制相互作用力的强度，对于Ｄ２Ｑ９模型，当

ｅ

＝

０时，Ｇ

σσ

＝

０；当ｅ

＝

１时，Ｇ

σσ

＝

Ｇ；当

ｅ

＝

２时，Ｇ

σσ

＝

Ｇ／４．对于非混相流体系统，

当

＝

时，Ｇ

＝

０；而当

≠

时，Ｇ为正值．通过

调节Ｇ的取值大小，可以调整流体之间的界面张

力的大小．

当考虑固体表面可润湿性对流体流动的影响

时，流体和表面相互作用力Ｆ

ｗ

（ｘ）可表示为

［１３］

Ｆ

ｗ

（ｘ）＝－

（ｘ）

∑

Ｇ

ｗ

ｓ（ｘ

＋

ｅ

）ｅ

（４）

其中ｓ的取值表征固相的存在，对于固相，ｓ

＝

１，

对于非固相，ｓ

＝

０．类似地，Ｇ

ｗ

是控制流体和表面

相互作用力强度的参数，对于Ｄ２Ｑ９模型，当

ｅ

＝

０时，Ｇ

ｗ

＝

０；当ｅ

＝

１时，Ｇ

ｗ

＝

Ｇ

ｗ

；当

ｅ

＝

２时，Ｇ

ｗ

＝

Ｇ

ｗ

／４．通常情况下，当流体为

非润湿流体时，Ｇ

ｗ

取正值；当流体为润湿性流体

时，Ｇ

ｗ

取负值．通过调节Ｇ

ｗ

的取值，可以得到不

同的表面润湿性条件．

粒子受到外力Ｆ

ｅ

（ｘ）表示为

Ｆ

ｅ

（ｘ）＝

ｇ

（５）

其中

ｇ

为单位质量力，如果是考虑重力的影响，则

ｇ

为重力加速度．

作用在流体粒子上作用力Ｆ

（ｘ）包括流体间

的相互作用力Ｆ

ｆ

（ｘ）、流体和表面间的作用力

Ｆ

ｗ

（ｘ），以及外力Ｆ

ｅ

（ｘ）．通过改变式（２）中平衡

态速度ｕ

ｅｑ

来体现Ｆ

（ｘ）的影响，即

ｕ

ｅｑ

＝

ｕ

′

＋

Ｆ

／

（６）

其中ｕ

′

定义为ｕ

′

＝

∑

ｕ

∑

，这样可保证

在没有作用力时碰撞过程动量守恒

［１２］

．

对于Ｄ２Ｑ９模型，混合流体的压力为

ｐ

（ｘ）＝

ｃ

２

ｓ

∑

（ｘ）＋

３

２

∑

，

Ｇ

σσ

（ｘ）

（ｘ），而流体的速度

定义为ｕ

＝

∑

ｕ

＋

∑

Ｆ

２

．

２　数值模拟

２．１　研究体系及边界条件

本文的研究对象为二维水平通道内的非混相

驱替过程．通道的长宽比为５ ∶ １，采用笛卡儿直

角坐标系，坐标原点位于通道的左下角，如图１所

示．研究区域划分为４００ × ８０个格子，所有物理量

均为格子单位，与实际物理单位可以通过归一化

处理进行相互转换．初始时，对于ｘ

≥

Ａ，通道内

充满了静止的流体２（被驱替流体）；而对于

０

≤

ｘ

＜

Ａ，通道内则为初始速度为ｕ的流体

１（驱替流体）．对于通道的上表面和下表面，采用

半步长反弹格式以实现无滑移的边界条件．入口

条件为恒定速度边界条件，出口条件为外推边界

条件．

２．２　界面张力的确定

伪势模型中，界面张力是根据Ｌａｐｌａｃｅ定律

确定的．根据Ｌａｐｌａｃｅ定律，气泡或液滴的曲率半

径和其内外的压力差满足 Δ

ｐ

＝

／Ｒ，其中参数

为界面张力．在１００

１００的格子系统内，最初，正

方形的流体２被流体１所环绕，不考虑外力作用，

系统最终演化到稳定状态．由于界面张力的作用，

流体２会呈现一个圆形液滴．图２给出了不同的

黏度比Ｍ下的压力差 Δ

ｐ

和曲率１／Ｒ的关系如图

４４３

大连理工大学学报

第５２卷　

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38612648

粉丝: 12
资源: 920

水平通道内黏性指进现象LBM模拟 (2012年)

最新资源

水平通道内黏性指进现象LBM模拟 (2012年)

微通道中液滴内部速度场的LBM模拟

LBM模拟容器内液体流动

多相流LBM模拟Fortran代码

LBM模拟多孔介质流

LBM.zip_LBM_LBM功能_LBM怎么编程_LBM模拟_politicalica

基于LBM的流动模拟

contactAngle2d_LBM_lbm接触角_LBM接触角_LBM，_二维接触角的LBM模拟

用LBM模拟泊肃叶流的流动特性，用的fortran

shanchen.zip_LBM两相_lbm 两相流模拟_matlab 两相流_shan-chen LBM_流

LBM模拟一维导热

LBM模拟二维平板流matlab代码

LBM模拟顶盖驱动流

contactAngle2d_LBM_lbm接触角_LBM接触角_LBM，_二维接触角的LBM模拟.zip

couette_flow_exam_Couetteflow_LBM_

phaseSeparation2d_LBM_LBM两相模拟_

lbm_LBM三维_三维LBM_lbm三维_LBM_

lbm模拟液滴从壁面滑落

back-step_基于LBM方法的后台阶驱动流模拟_格子玻尔兹曼_back_后台阶_

顶盖驱动流LBM模拟.rar_LBM_return3i7_顶盖驱动_顶盖驱动流_驱动模拟

Nils 关于LBM模拟倒水的文章

泊肃叶流LBM模拟

MATLAB.rar_LBM两相_lbm双_matlab 两相流_societynvx_双流体

contactAngle2d_LBM_lbm接触角_LBM接触角_LBM，_二维接触角的LBM模拟_源码.rar

LBM模拟圆柱绕流

LBM代码 - 副本.zip_LBM_deep4cn_lbm扰流_lbm用C语言_管流

chapter4c_zip_LBM_LBM多相流_LBM多相流_matlab

有限差分LBM模拟方腔流C++

一种基于LBM的气液固三相流多尺度模拟方法

C++LBM顶盖驱动流.rar_LBM_LBM流动模拟_lbm c_顶盖驱动_顶盖驱动流

最新资源