没有合适的资源?快使用搜索试试~ 我知道了~
FuzzyEn算法在混沌序列复杂度分析中的应用
0 下载量 173 浏览量
2021-03-11
20:03:35
上传
评论
收藏 634KB PDF 举报
温馨提示
为了正确地分析混沌序列的复杂度,基于FuzzyEn算法研究了系统的复杂度,包括典型的离散混沌系统和连续混沌系统。 与ApEn,SampEn和密集统计复杂度算法相比,FuzzyEn算法是一种分析混沌序列复杂度的有效度量算法,它对相空间维数(m),相近容差(r)和序列长度具有较低的敏感性和较小的依赖性。 (N),具有更好的鲁棒性和度量值连续性。混沌系统的复杂度结果表明,连续混沌系统的复杂度比离散混沌系统的复杂度小得多。 但是,连续混沌系统的伪随机序列受到高复杂度离散混沌伪随机序列或经典m系列的干扰,大大增加了它们的复杂度。 我们的结果为混沌序列在密码学和安全通信领域的应用提供了理论基础。
资源推荐
资源详情
资源评论

Ô n Æ Acta Phys. Sin. Vol. 61, No. 13 (2012) 130507
{{{333···bbbSSSEEE,,,ÝÝÝ©©©ÛÛÛ¥¥¥AAA^^^
*
1)2)†
åÅ
1)
Ùf
1)
C/å · õå%
2)
1) ( ¥HÆÔnÆEâÆ, â 410083 )
2) ( #õÆÔnÆEâÆ, ¿°7à 830046 )
( 2011 c 11 7 FÂ; 2011 c 12 5 FÂ?Uv )
O(©Û·bSE,5, æ^{ (FuzzyEn) é;.lÑ·bXÚÚëY·bXÚE,Ý?
1©Û. Cq (ApEn)! (SampEn) ÚrÝÚOE,Ý{', FuzzyEn {´«k·bE,
ÝÿÝ{, émê (m)!qNÝ (r) ÚSÝ (N ) ¯a5! 65$, °5ÚÿÝë
Y5Ð. é·bXÚE, 5©ÛL², ëY·bXÚE,ÝulÑ·bXÚ, ´X J|^pE,Ý
lÑ·bÅS½²; m SéëY·bXÚ)ÅS?16Ä, KUJp·bS E,5.
·bS3èÆÚ·bÏ&¥A^JønØâ.
'c: , lÑ·bXÚ, ëY·bXÚ, E,Ý
PACS: 05.45.Tp, 05.45.−a
1 Ú ó
·bSE,5®²¤&ES+
ïÄ
[1,2]
, ¿Úå2'5. S
E,5, ÙÅ5Ò, SU¡E
JÝÒ. ¢^·bSAäk¦U
E,5, ±y*ªÏ&XÚ|Z6Ú|
¼Uå
[3]
. 8c, ·bSE,ÝÿÝ{¦^
õ´ Pincus JÑCq (ApEn) {
[4]
Ú Richman <JÑ Cq U ?{ -
(SampEn) {
[5]
, üöq5þÝæ^ Heav-
iside ¼ê, éK r Úmê m ~
¯a, SampEn ØOgÚOþ, Ï
´#&E)ÿÝ, ù´é ApEn U?,
3ùe¬Ñyÿ ln 0. d,
©z [6,7] JÑ|^rÝÚOE,Ý {O ·b
SE,Ý, T{äkëê!éëê¯a5
A:, ´é±ÏSE ,ÝØUéÐÝþ. ©
z [8,9] JÑ^ÎÒ ÿþ·bÅS{,
T{?Úü$ëêÀéÿÝ(JK,
ÎÒ{I¯kÎÒm, é
ÅS, ùÙ¢^5. 2007 c, ©z [10,
11] é (SampEn) ?1 U?, ÄgJÑ
(FuzzyEn) {, ¿¤õòÙA^uL¡*>
&ÒJ©a, ©z [12] ?Ø FuzzyEn {
élÑ·bXÚE,Ý©Ûk5.
©ò FuzzyEn {A^u·bXÚE,Ý
©Û. Äk©Û FuzzyEn {A59ÙëêÀJ
K, ,ò FuzzyEn {©OA^ulÑ·bX
ÚÚëY· bXÚE,5 ©Û, ?Ø ·b
ÅS 6ÄcE, ÝCz5Æ, ·b
èÆ·bÏ&JønØâ.
2 {n£ã
2.1 ½½½ÂÂÂ
éu½mS [u(1), u(2), · · · , u(N)],
Ú\Kê m(m 6 N − 2), é u ?1 m
,
[11]
s
m
[i] = {u(i), u(i + 1), · · · , u(i + m − 1)} − u
0
(i),
(1)
*
I[g,ÆÄ7 (1OÒ: 61161006, 61073187) ]ÏK.
†
E-mail: kehui@csu.edu.cn
c
° 2012 ¥¥¥IIIÔÔÔnnnÆÆƬ¬¬ Chinese Physical Society http://wulixb.iphy.ac.cn
130507-1
Ô n Æ Acta Phys. Sin. Vol. 61, No. 13 (2012) 130507
Ù¥ i = 1, 2, · · · , N − m + 1, u
0
(i)
u
0
(i) =
1
m
m−1
∑
j=0
u(i + j). (2)
Ú\äá¼ê
[12]
A(x) =
1, x = 0
exp
[
− ln(2)
(
x
r
)
2
]
, x > 0
(3)
Ù¥ r qNÝ, ⪠(3), -äá¼ê
A
m
ij
= exp(− ln(2) · (d
m
ij
/r)
2
), (4)
Ù¥
d
m
ij
=d[s
m
[i], s
m
[j]]
= max
p=1,2,··· ,m
(|u(i + p − 1) − u
0
(i)|
− |u(j + p − 1) − u
0
(j)|). (5)
Iþ s
m
[i] Ú s
m
[j] mål, ù
C
m
i
(r) = (N − m)
−1
N−m+1
∑
j=1,j6=i
A
m
ij
. (6)
=
Φ
m
(r) = (N − m + 1)
−1
N−m+1
∑
i=1
C
m
i
(r). (7)
Ïd, ½Â·b (Å) S (Fuzzy en-
tropy)
FuzzyEn(m, r, N) = ln Φ
m
(r) − ln Φ
m+1
(r), (8)
Ù¥, ëê m, r, N ©Omê! qN
Ý! mSÝ. Ï~¹e, m U[
XÚÄüzL§. qN r
´ įK, LqN¬
&E¿, qN, ¿&Eõ,
qNÝK¬O\(JéD(¯a5,
½Â r r
∗
SD
[4]
, Ù¥ SD(Standard Deviation)
mSIO, 3¡?Ø¥,
XJ`qNÝ r = 0.3, KL« r = 0.3
∗
SD, Ù
¦gaí. CqÚÔn¿Âq,
ïþ´#ª)VÇ, ÿÝ
, #ª)VÇ, =SE,Ý.
2.2 FuzzyEn {{{ëëëêêêÀÀÀJJJ©©©ÛÛÛ
ÜnÀ FuzzyEn {ëê, é·bX
ÚE,ÝÿÁXÚ?1©Û, ÿÁXÚæ^ TD-
ERCS XÚ
[13]
, XÚ«fëê (0.7123, 0.7654,
0.9876, M), SÝ N = 1000, Ù¥ M ò
´ëê. e¡©Oæ^ FuzzyEn, SampEn Ú ApEn
{, ©Ûò´ M 0, 2 Ú 4 , ëê m Ú r
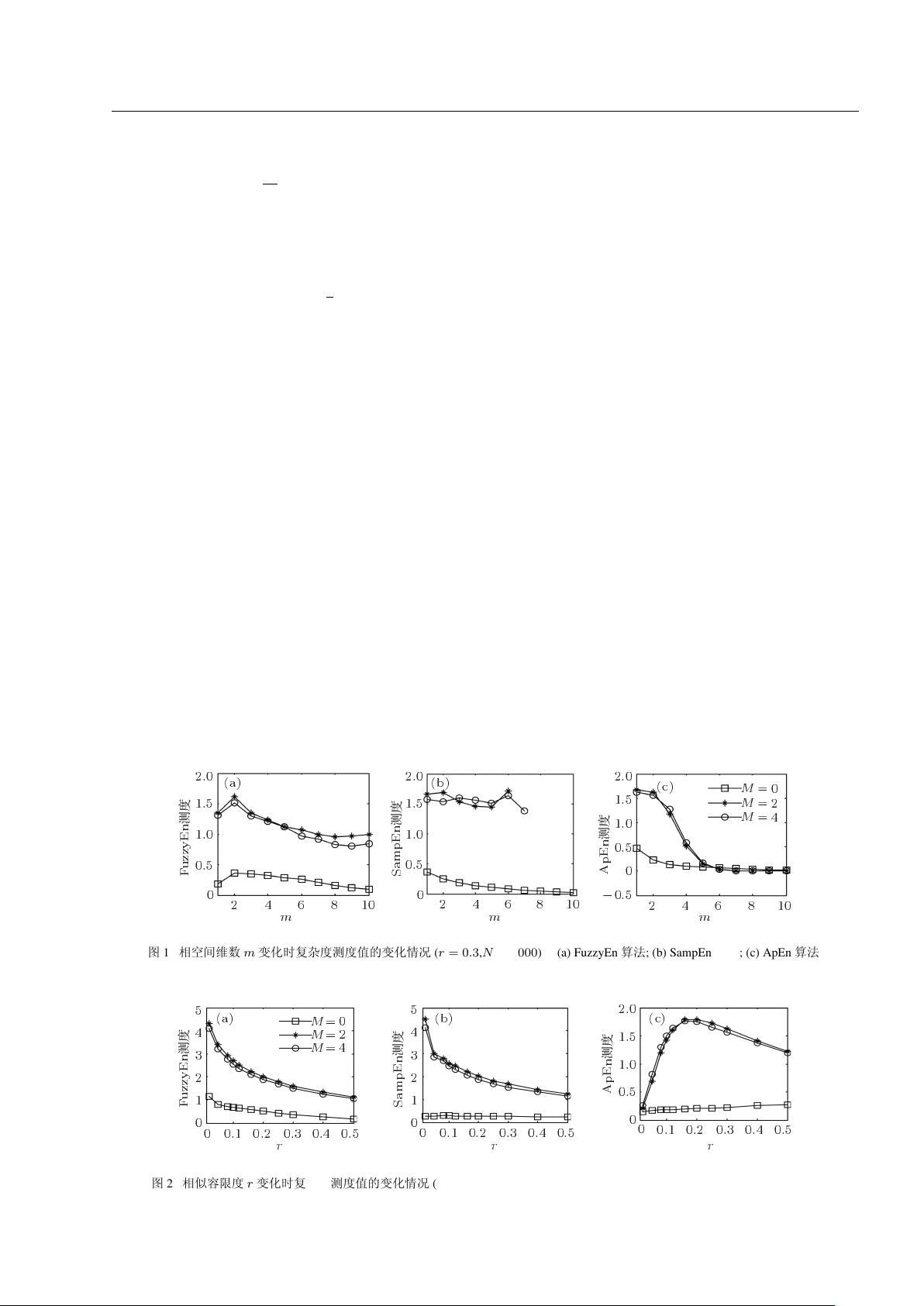
CzéE,ÝÿÝK, Ù(JXã 1 Ú 2 ¤«.
ã 1 mê m CzE,ÝÿÝCz¹ (r = 0.3,N = 1000) (a) FuzzyEn {; (b) SampEn {; (c) ApEn {
ã 2 qNÝ r CzE,ÝÿÝCz¹ (m = 2, N = 1000) (a) FuzzyEn {; (b) SampEn {; (c) ApEn {
130507-2
剩余6页未读,继续阅读
资源评论

weixin_38612648
- 粉丝: 12
- 资源: 920
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功