非均匀采样有很多种,一般来说只要采样间隔不是恒定的,就可以认为是非均匀采样,但是对于大多数非均匀采样其并不具有特别的性能。本案例研究的非均匀采样特指两种情况:随机采样和伪随机采样。随机采样中每个采样点的选择是完全随机的,是理想化的非均匀采样;伪随机采样中每个采样点的选择是经过挑选的伪随机数。非均匀采样的一个很大的优点就是它具有抗频率混叠的性能,从而可以突破奈奎斯特频率的限制,实现以比较低的采样频率检测到很高频率的信号。 采样时刻的选择无疑是非常重要的,它决定了采样后得到的信号的性质。时钟抖动的均匀采样在工程实践中是普遍存在的,并且是不可避免的,例如AD时钟频率存在一定偏差。有抖动的均匀采 非均匀采样是一种在信号处理领域中用于克服传统均匀采样限制的技术,特别是在单片机与数字信号处理器(DSP)的应用中。与均匀采样即按照恒定时间间隔获取信号样本不同,非均匀采样允许采样间隔变化,以此来对抗频率混叠现象并可能提高信号恢复的质量。 本案例主要探讨了两种非均匀采样类型:随机采样和伪随机采样。随机采样是基于完全随机选取的采样点,这是一种理想的非均匀采样方式。而伪随机采样则是利用精心挑选的伪随机数序列来确定采样点,这种方法在实践中更易控制和实现。 非均匀采样的关键优势在于其能抵抗频率混叠。根据香农采样定理,为了无失真地恢复一个信号,采样频率需至少是信号最高频率的两倍,即奈奎斯特频率。然而,非均匀采样可以突破这一限制,即便采样频率较低,也能有效地识别高频信号,这是因为非均匀采样改变了信号的频谱结构,降低了频率混叠的风险。 采样时刻的选择至关重要,因为它直接影响到采样后信号的特性。在实际工程应用中,如ADC(模数转换器)的时钟频率可能存在偏差,导致有抖动的均匀采样,这可能导致采样点过于集中或稀疏,对信号恢复产生不利影响。均匀采样中的时钟抖动可以通过数学模型来描述,例如,采样时刻tk可以用一个服从特定概率分布的随机变量来表示。 加性非均匀采样是另一种非均匀采样形式,其中当前的采样时刻依赖于之前的采样时刻。随着采样次数的增加,采样点的概率分布趋向于平坦,这有助于避免频率混叠,并可能使信号恢复更加准确。根据中心极限定理,当采样次数足够大时,采样点的分布将接近正态分布。 通过对比均匀采样和非均匀采样,我们可以看到非均匀采样如何消除频率混叠。例如,当一个低频正弦信号被不均匀地采样时,采样点不再均匀分布,这使得只有原始信号能通过这些点,从而有效地排除了其他频率成分的干扰。这在图3中得到了直观展示,非均匀采样可以保持信号的可识别性,即使采样频率低于奈奎斯特频率。 总结来说,非均匀采样是信号处理领域的一种创新技术,它提供了一种在低采样率下捕获和恢复高频率信号的可能性,这对于资源受限的单片机和DSP系统尤其重要。通过对随机和伪随机采样的研究,以及深入理解采样时刻选择的影响,工程师可以设计出更有效的信号处理算法,以应对各种复杂信号环境中的挑战。

- 粉丝: 4
- 资源: 933
 我的内容管理
展开
我的内容管理
展开
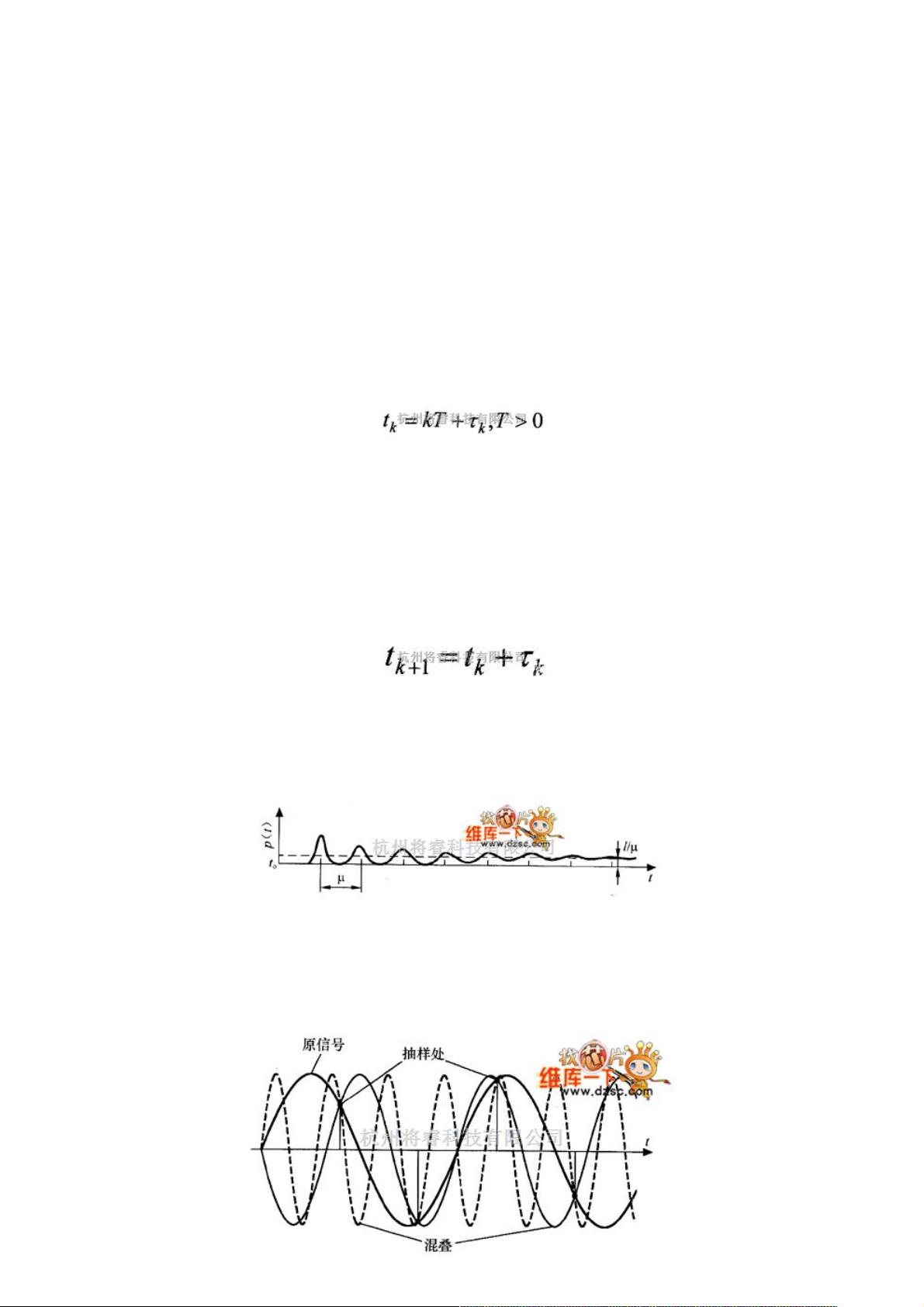
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 【岗位说明】公司行政岗位职责.doc
- 【岗位说明】公司行政副总岗位说明书.doc
- 【岗位说明】公司行政文职类岗位职责.doc
- 【岗位说明】行政部岗位职责.doc
- 【岗位说明】公司组织结构及部门职责.doc
- 【岗位说明】行政部锅炉工岗位说明书.doc
- 【岗位说明】行政部各职位说明书.doc
- 【岗位说明】行政部门岗位职责02.doc
- 【岗位说明】行政后勤岗位职责.doc
- 【岗位说明】行政经理岗位说明书.doc
- 【岗位说明】行政前台岗位职责.doc
- 【岗位说明】行政经理岗位职责.doc
- 【岗位说明】行政前台岗位职责及工作要求.doc
- 【岗位说明】行政人事部部门职责(制造业).doc
- 【岗位说明】行政人事部部门职责说明书(计算机企业).doc
- 【岗位说明】行政人事部部门职责说明书(旅游公司).doc


 信息提交成功
信息提交成功