用于存储环中振荡电偶极矩测量的统计灵敏度估计资源-CSDN文库

Open

Access

39 浏览量 2020-03-22 05:24:01 上传评论收藏 1.45MB PDF 举报

资源推荐

资源详情

资源评论

Eur. Phys. J. C (2020) 80:107

https://doi.org/10.1140/epjc/s10052-020-7664-9

Regular Article - Experimental Physics

Statistical sensitivity estimates for oscillating electric dipole

moment measurements in storage rings

J. Pretz

1,2,3,a

, S. P. Chang

4,5

, V. Hejny

, S. Karanth

, S. Park

, Y. Semertzidis

4,5

, E. Stephenson

, H. Ströher

1,8

Institut für Kernphysik, Forschungszentrum Jülich, 52425 Jülich, Germany

III. Physikalisches Institut B, RWTH Aachen University, 52056 Aachen, Germany

JARA-FAME, Forschungszentrum Jülich, RWTH Aachen University, Aachen, Germany

Center for Axion and Precision Physics Research, IBS, Daejeon 34051, Republic of Korea

Department of Physics, KAIST, Daejeon 34141, Republic of Korea

Marian Smoluchowski Institute of Physics, Jagiellionian Univsersity, Cracow, Poland

Indiana Univ., Bloomington, IN 47408, USA

JARA–FAME (Forces and Matter Experiments), Forschungszentrum Jülich, RWTH Aachen University, Aachen, Germany

Received: 4 December 2019 / Accepted: 19 January 2020

Abstract In this paper analytical expressions are derived to

describe the spin motion of a particle in magnetic and electric

ﬁelds in the presence of an axion ﬁeld causing an oscillat-

ing electric dipole moment (EDM). These equations are used

to estimate statistical sensitivities for axion searches at stor-

age rings. The estimates obtained from the analytic expres-

sions are compared to numerical estimates from simulations

in Chang et al. (Phys Rev D 99(8):083002, 2019). A good

agreement is found.

1 Introduction and motivation

Axions and axion like particles (ALPs) are candidates for

dark matter. There is thus a huge experimental effort for the

search of these kind of particles. For a detailed review, we

refer the reader to references [2,3]. Axions and ALPs can

interact with ordinary matter in various ways. Reference [4]

identiﬁes three terms:

μν

∂

Ψ (1)

describing the coupling to photons, gluons and to the spin

of fermions, respectively. The vast majority of experi-

ments makes use of the ﬁrst term [e.g. Cavity experiments

(ADMX), helioscopes (CAST), light-through-wall experi-

ments (ALPS)]. In addition, astrophysical observations also

provide sensitive limits to the axion-photon coupling. In gen-

eral, it is rather difﬁcult for these experiments to reach masses

below 10

−6

eV, one reason being that the axion wave length

e-mail: pretz@physik.rwth-aachen.de

becomes too large. Furthermore, these experiments are mea-

suring rates proportional to at least a small amplitude squared.

For the second (and third) term in the list (1)thisisdiffer-

ent. It turns out that the second term has the same structure

as the QCD-θ term which is also responsible for an electric

dipole moment (EDM) of nucleons. The axion ﬁeld gives

rise to an effective time-dependent θ -term and oscillates at

a frequency proportional to the mass of the axion m

.This

gives rise to an oscillating EDM. New opportunities to search

for axions/ALPs with much higher sensitivity arise, because

the signal is proportional to an amplitude A and not to its

square. To date, NMR based methods are being used to look

at oscillating EDMs [5].

Another possibility is to search for axions/ALPs in stor-

age rings. Storage ring experiments have been proposed to

search for electric dipole moments of charge particles [6,7].

These experiments allow also, with small modiﬁcations, to

search for oscillating EDMs. This possibility is discussed

in this paper. Section 2 explains the principle of the exper-

iment, how the (oscillating) EDM alters the spin motion in

electromagnetic ﬁelds and leads to a polarization observable.

In Sect. 3 statistical sensitivities for oscillating EDMs based

on these polarization observables are presented.

2 Spin motion in storage rings

The spin motion relative to the momentum vector in elec-

tric and magnetic ﬁelds is governed by the Thomas-BMT

equation [8–10]:

= (

MDM

+ 

EDM

) × S, (2)

0123456789().: V,-vol

123

107 Page 2 of 8 Eur. Phys. J. C (2020) 80:107



MDM

=−



GB −



G −

− 1



β × E



, (3)



EDM

=−

ηq

2mc

[

E + cβ × B

]

. (4)

S in this equation denotes the spin vector in the particle rest

frame, t the time in the laboratory system, β and γ the rela-

tivistic Lorentz factors, and B and E the magnetic and electric

ﬁelds in the laboratory system, respectively. The magnetic

dipole moment μ and electric dipole moment d both point-

ing in the direction of the particle’s spin S are related to the

dimensionless quantities G (magnetic anomaly) and η in Eq.

μ = g

S = (1 + G)

S and d = η

2mc

S. (5)

We assume a vertical magnetic ﬁeld and a radial electric

ﬁeld, constant in time, forcing the particle on a circular orbit.

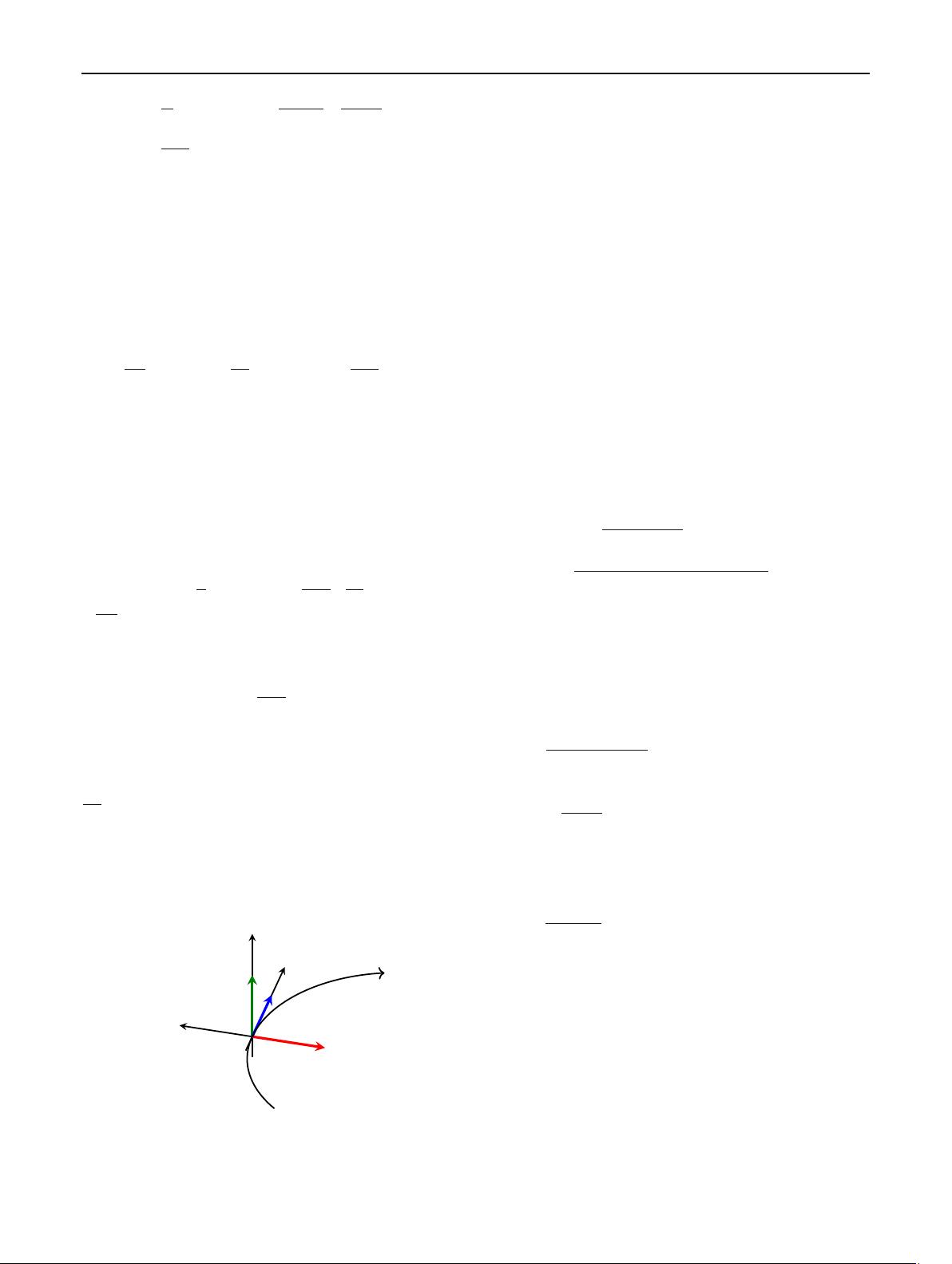
The three vectors B, E and v = βc are thus mutually orthog-

onal, as indicated in Fig. 1. In this case



MDM

⎛

⎝

MDM

⎞

⎠

and 

EDM

⎛

⎝

EDM

⎞

⎠

(6)

with Ω

MDM

=−

(GB +



G −

−1



β E

) and

EDM

−

2mc

(E + cβ B), B =|B| and E =|E|. The coordinate

system is chosen such that the ﬁrst component points in radial

direction, the second in vertical and the third in longitudinal

direction. Note that β ×E is anti-parallel to B. This explains

the +sign in front of



G −

−1



in the deﬁnition of Ω

MDM

instead of a − sign in Eq. 3.

For the following discussion it is more convenient to write

Eq. 2 in matrix form:

(

MDM

+ A

EDM

)

S (7)

with (to simplify the notation we use Ω

EDM

instead of

EDM

from now on)

longitudinal

radial

vertical



v

Fig. 1 Illustration of the coordinate system used

MDM

⎛

⎝

00Ω

MDM

000

−Ω

MDM

⎞

⎠

and A

EDM

= η

⎛

⎝

00 0

00Ω

EDM

0 −Ω

EDM

⎞

⎠

. (8)

In the following we assume that the EDM can have a

constant term and a time varying component, thus η = η

cos(ω

t +ϕ

) as suggested in [4,11]. The oscillating term

is caused by an axion of mass given by the relation ω

h. Assuming η

,η

 G, A

EDM

in Eq. 7 can be treated

as a perturbation.

The solution to ﬁrst order in η

and η

for arbitrary ini-

tial condition of the spin is given in Appendix A. The best

sensitivity to η

and η

is obtained by observing a build-

up of a vertical polarization of a beam initially polarized in

the horizontal plane. Thus we are interested in the behavior

of the vertical spin component S

(t) in the case where the

spin points for example initially in the longitudinal direction

(S(0) = (0, 0, 1)

). Using Eq. 37 in Appendix A one ﬁnds:

(t) = η

EDM

sin(Ω

MDM

+η

EDM

2(ω

− Ω

MDM

)(Ω

MDM

+ ω

)

[

−2ω

sin(ϕ

)

+(ω

+ Ω

MDM

) sin

(

(ω

− Ω

MDM

)t + ϕ

)

+(ω

− Ω

MDM

) sin

(

(Ω

MDM

+ ω

)t + ϕ

)

]

. (9)

We are interested in the behavior close to the resonance

condition Ω

MDM

≈ ω

. Ignoring in Eq. 9 all fast oscillating

terms (i.e. assuming Ω

MDM

,(Ω

MDM

+ω

)  Ω

MDM

−ω

)

one ﬁnds

(t) =

EDM

2(ω

− Ω

MDM

)

(

−sin(ϕ

) + sin

(

(ω

− Ω

MDM

)t + ϕ

))

. (10)

= η

EDM

2Δω

(

−sin(ϕ

) + sin(Δωt + ϕ

)

(11)

with Δω = ω

−Ω

MDM

For ϕ

= 0 this expression coincides

with the expression given for NMR experiments [5]. At the

resonance, ω

= Ω

MDM

,Eq.11 reduces to

(t) =

EDM

cos(ϕ

) t. (12)

In this case the build-up is linear in time to ﬁrst order in η

The phase ϕ

of the axion ﬁeld is unknown. The experi-

ment should be performed with two bunches in the ring where

the polarizations are orthogonal to each other, which corre-

sponds to two phases ϕ

and ϕ

+ π/2. This assures not

to miss an axion signal. This can also be seen in Fig. 2.It

shows the build-up of the vertical spin component S

as a

function of time t for ϕ

= 0 and ϕ

= π/2 and for dif-

ferent axion frequencies ω

and Ω

MDM

= 750,000.0s

−1

This Ω

MDM

corresponds to typical running conditions with

123

剩余7页未读，继续阅读

评论收藏

内容反馈

weixin_38598613

粉丝: 7
资源: 914

用于存储环中振荡电偶极矩测量的统计灵敏度估计

中子的永久电偶极矩的测量

介子$$ {{{\ varvec {g}}} $$ g –2中恒定径向磁场的校正和存储环中的电偶极矩实验

轻子电偶极矩和强烈的CP违规

轴突暗物质引起的振荡核电偶极矩产生原子和分子电偶极矩以及核自旋旋转

在大型强子对撞机中寻找奇异和重子重子的电偶极矩

大规模超对称模型中的核子电偶极矩

在大型强子对撞机上使用弯曲晶体测量τ轻子电磁偶极矩的可行性

反向跷跷板模型中的电子电偶极矩

磁共振的一般经典和量子力学描述：在电偶极矩实验中的应用

有效场论，电偶极矩和电弱重生

违反CP的BLMSSM中的c（t）电偶极矩的单环贡献

食管后重子产生的电偶极矩

引力对μ子偶极矩测量的影响

在电弱相互作用的大型粒子模型中，重归一化对电偶极矩的影响

与宇宙的重子不对称有关的电子偶极矩的抵消机制

matlab结题报告(电偶极子的辐射场).docx

来自暗区的电偶极矩

夸克电偶极矩的实验约束

QCD中重张量介子的磁偶极矩

违反CP的夸克Yukawas的电偶极矩约束

Di通过辐射轻子衰变的偶极矩

偶极矩介电常数.doc

在电场和磁场作用下磁偶极矩的平面量子动力学

溶液法测定极性分子偶极矩的数据处理方法.pdf

通过CLIC的单顶生产，电磁偶极矩的界限

振荡电偶极子辐射电磁波CAI动画显示技术研究.pdf

实验二十九偶极矩的测定.doc

最新资源