Solution of a Class of Minimal Surface Problem with Obstacle

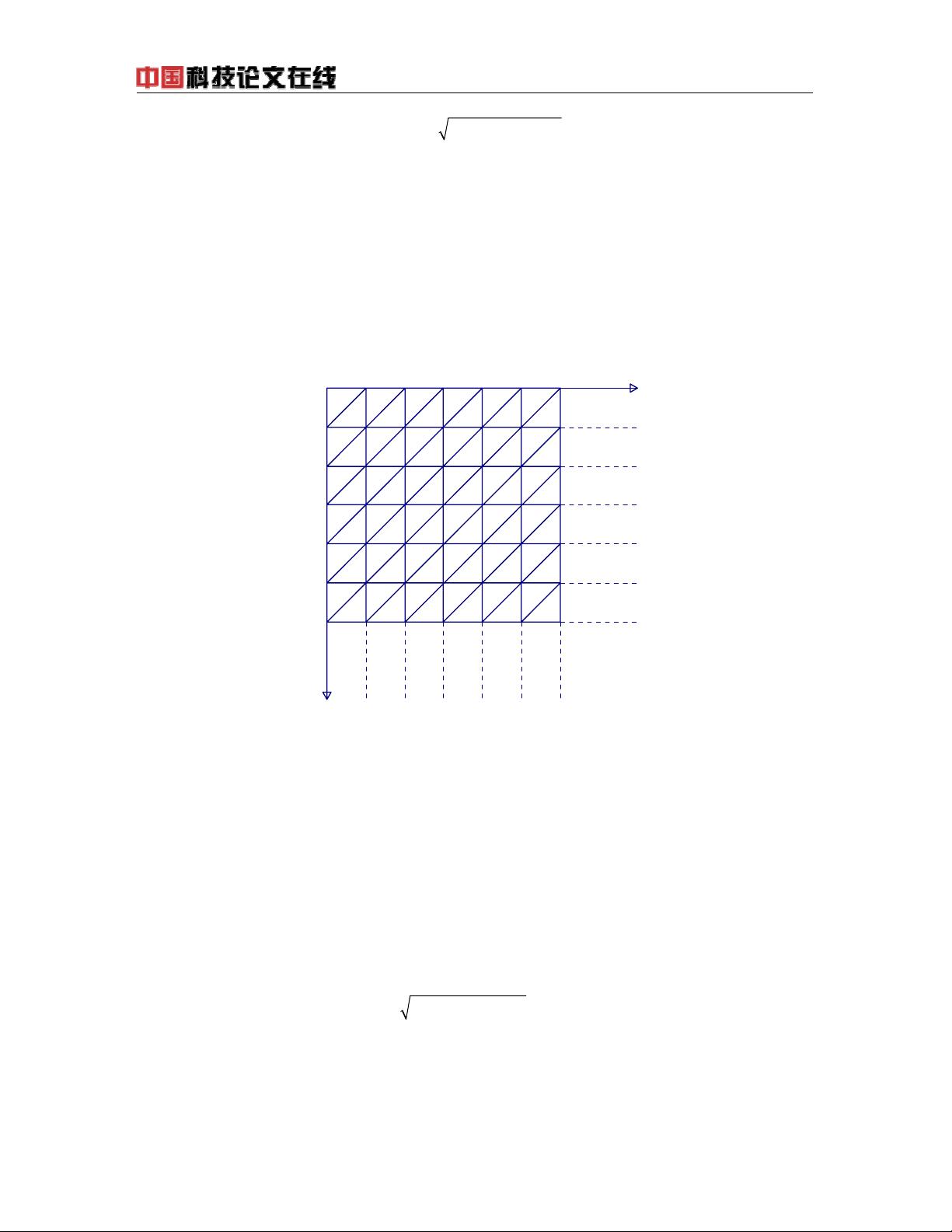
本文讨论的是一类特定的数学物理问题，即在存在障碍物条件下的极小曲面问题的求解方法。极小曲面问题是一种经典的变分问题，它在数学物理领域有着广泛的应用。Plateau问题便是这类问题中的一个典型例子，它旨在确定一个具有最小表面积的曲面，该曲面穿过给定的一个闭合曲线，并位于某个障碍物之上。此类问题在流体力学、材料科学、计算机图形学等多个领域中都有非常重要的地位。 文章中提到的作者刘克飞、李尚志和Wang Min来自北京航空航天大学的数学系和计算机科学与工程学院。他们提出了一个具体的例子，并应用有限元法来求解该问题。有限元法是现代数值分析中一种非常强大的工具，它将连续的数学模型划分为有限个小元素，通过求解这些小元素上的问题，来近似原始连续模型的解。在本问题中，这涉及将定义域三角化，并最小化某函数在分段线性函数空间上的值。 在有限元方法的应用中，计算结果的精度、计算时间与网格数量之间的关系被详细讨论。这涉及到选择合适的网格密度，既不能过大，导致计算量剧增，也不能太小，以致于无法达到所需的精度。文章中也引入了序贯二次规划法（Sequential Quadratic Programming, SQP）作为求解约束非线性优化问题的一个高效方法。序贯二次规划法是一种迭代算法，它通过求解一系列的二次规划子问题来逼近非线性约束问题的最优解。该方法的实现利用了MATLAB优化工具箱中的fmincon函数。 研究中还对Plateau问题进行了解析和数值上的探讨，提出了极小曲面的非参数形式表示，并对障碍物条件下的解的存在性和唯一性进行了证明。文中提及的数学函数和表示，如L2范数、R→R的函数f以及边界数据的梯度空间H(D)等，都是现代数学分析的常客。通过对这些数学概念的运用，作者能够构建和分析极小曲面问题的数值解。 序贯二次规划法之所以被选用，是因为其在处理有约束条件的非线性优化问题时，相较于其他方法，能更好地保证计算的稳定性和收敛速度。这种方法在工程和科学计算领域非常受欢迎，因为它可以有效处理包括等式约束和不等式约束在内的多种约束条件。 为了说明该方法的有效性，文章还讨论了不同网格数量对计算时间和解的精度的影响。这是数值分析和计算数学研究中的一个核心问题，如何平衡计算效率和解的精度是一个永恒的挑战。 本文提供了一种在存在障碍物的条件下求解Plateau问题的有效方法。通过有限元方法和序贯二次规划法的结合，给出了一个既实用又具有理论价值的数值解法。这种方法不仅能够得到较为精确的数值结果，而且在计算效率上也有不错的表现。对于那些对现代数学物理、数值分析以及优化算法感兴趣的读者，本研究提供了一次深入了解相关领域的宝贵机会。