Two-DimensionalDOAEstimationforIncoherentlyDistributedSourceswithUniformRectangularArrays.资源-CSDN文库

82 浏览量 2021-02-07 01:02:45 上传评论收藏 472KB PDF 举报

### 两维到达角（DOA）估计方法用于非相干分布源与均匀矩形阵列 #### 摘要及背景介绍本文提出了一种基于均匀矩形阵列（Uniform Rectangular Array, URA）的二维（2D）非相干分布（Incoherently Distributed, ID）源的到达角（Direction of Arrival, DOA）估计算法。通过泰勒级数展开方向矢量的方法，在小角度扩散和传感器间距离较小的假设下推导了名义方位角和名义仰角之间的子阵列旋转不变关系。由此，接收信号向量可由广义方向矩阵和广义信号向量表示；因此，提出了一个类似Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT)的算法来分别估计名义仰角和名义方位角，利用构建的子阵列的协方差矩阵。通过Capon原理提出了角匹配方法。所提出的算法无需进行谱搜索即可估计多个2D非相干分布源，并且不需要源的角度功率分布信息。 #### 关键技术要点分析 **1. 非相干分布源与广义方向矩阵：** 非相干分布源是指在一定空间范围内，信号源的能量不集中于一点，而是分散在一个区域内。这种情况下，传统的点源模型不再适用。文中提到的广义方向矩阵是通过考虑信号源的能量分布在一定范围内的特性而建立的。通过引入广义方向矩阵，可以更准确地描述信号传播路径，提高DOA估计精度。 **2. 子阵列旋转不变关系：** 子阵列旋转不变关系是通过泰勒级数展开方向矢量的方法得到的，它反映了不同子阵列间的信号特性在特定条件下保持不变的性质。这种性质对于实现精确的DOA估计至关重要。通过这种方法，即使在角度扩散较大的情况下，也能有效地提取出有用的信号特征。 **3. ESPRIT算法的应用：** ESPRIT算法是一种基于信号子空间分解的参数估计方法，特别适用于处理具有旋转不变特性的信号。本文提出的类似ESPRIT的算法能够利用子阵列的协方差矩阵来进行DOA估计，从而避免了复杂的谱搜索过程，提高了计算效率和估计准确性。 **4. 角匹配方法与Capon原理：** 角匹配方法是利用Capon原理进行的一种后处理步骤，用于进一步优化DOA估计结果。Capon原理通常被用来减少噪声的影响并提高信号分辨率。通过将Capon原理应用于角匹配过程中，可以提高估计的准确性，特别是在复杂环境中。 #### 实验验证与讨论为了验证所提方法的有效性，文中进行了多种情况下的模拟实验，包括不同信噪比（Signal to Noise Ratio, SNR）、不同角度功率密度函数、边界区域源以及不同传感器间距等条件。这些实验结果表明，所提方法能够在多种情况下提供准确的DOA估计，尤其是在处理多个非相干分布源时表现出良好的性能。本文提出的基于均匀矩形阵列的2D非相干分布源DOA估计方法为解决实际应用场景中的复杂信号处理问题提供了一个有效解决方案。该方法不仅避免了谱搜索过程，而且不需要源的角度功率分布信息，使得其实用性和灵活性得到了显著提升。

资源推荐

资源详情

资源评论

sensors

Article

Two-Dimensional DOA Estimation for Incoherently

Distributed Sources with Uniform Rectangular Arrays

Tao Wu

*, Zhenghong Deng

*, Yiwen Li

and Yijie Huang

School of Automation, Northwestern Polytechnical University, Xi’an 710072, China; hyjrly@126.com

Science and Technology on Combustion, Thermal-Structure and Internal Flow Laboratory,

Northwestern Polytechnical University, Xi’an 710072, China; lee_yiwen@nwpu.edu.cn

Correspondence: taowu_nwpu@126.com (T.W.); dthree@nwpu.edu.cn (Z.D.); Tel.: +86-150-2988-2069 (T.W.)

Received: 22 August 2018; Accepted: 18 October 2018; Published: 23 October 2018



 

Abstract:

Aiming at the two-dimensional (2D) incoherently distributed (ID) sources, we explore

a direction-of-arrival (DOA) estimation algorithm based on uniform rectangular arrays (URA).

By means of Taylor series expansion of steering vector, rotational invariance relations with regard

to nominal azimuth and nominal elevation between subarrays are deduced under the assumption

of small angular spreads and small sensors distance ﬁrstly; then received signal vectors can be

described by generalized steering matrices and generalized signal vectors; thus, an estimation of

signal parameters via rotational invariance techniques (ESPRIT) like algorithm is proposed to estimate

nominal elevation and nominal azimuth respectively using covariance matrices of constructed

subarrays. Angle matching method is proposed by virtue of Capon principle lastly. The proposed

method can estimate multiple 2D ID sources without spectral searching and without information of

angular power distribution function of sources. Investigating different SNR, sources with different

angular power density functions, sources in boundary region, distance between sensors and number

of sources, simulations are conducted to investigate the effectiveness of the proposed method.

Keywords:

incoherently distributed sources; generalized steering matrix; generalized signal vector;

rotational invariance relations; angle matching

1. Introduction

In most applications of array signal processing, traditional DOA estimation is based on point

source models which can simplify calculations. Point source models assume that propagations between

sources and receive arrays are straight paths and the spatial characteristics of sources can be ignored.

In the ﬁeld of wireless communication, there are obstacles around sources; the propagations from

sources to receive arrays are multipath. In the real surrounding of underwater, on the one hand,

there exist paths from seabed and sea surface of backscatters; on the other hand, spatial scatterers of

targets cannot be ignored when the distances from targets and receive arrays are short. Considering

the spatial scatterers and multipath phenomena, point models cannot characterize sources effectively,

which should be described by distributed source models [

]. The signal of a source only propagates

from a single direction through a straight path under the assumption of point source model. Distributed

sources can be regarded as an assembly of point sources within a spatial distribution. The shape of

spatial distribution is related to geometry and surface property of a target in underwater detection for

instance. Spatial distribution of a distributed source can be generally modeled as Gaussian or uniform

with parameters containing nominal angles and angular spreads. Nominal angles represent the center

of targets and angular spreads represent the spatial extension of targets.

According to the scatterers coherence of sources, distributed sources can be classiﬁed into

coherently distributed (CD) sources and incoherently distributed (ID) sources [

]. CD sources suppose

Sensors 2018, 18, 3600; doi:10.3390/s18113600 www.mdpi.com/journal/sensors

Sensors 2018, 18, 3600 2 of 18

that scatterers within a source are coherent whereas scatterers of an ID source are assumed to be

uncorrelated. In this paper, ID sources are considered.

For CD sources, representative achievements of DOA estimation are methods extended from point

source models through rotation invariance relations with respect to different array conﬁguration under

the small angular spreads assumption [

–

]. As to ID sources, people have presented subspace-based

algorithms such as distributed signal parameter estimator (DSPE) [

] and dispersed signal parametric

estimation (DSPARE) [

] which are developed from multiple signal classiﬁcation (MUSIC). Based on

uniform linear arrays (ULA), the authors of [

] have extended Capon method for ID sources,

where two-dimensional (2D) spectral searches based on high-order matrix inversion are involved.

The authors of [

] have proposed a generalized Capon’s method by introducing a matrix pencil of

sample covariance matrix and normalized covariance matrix to traditional Capon framework. A robust

generalized Capon’s method in [

] has been proposed by supplementing a constraint function using

property of covariance matrix to cost function of algorithm in [

], which has better accuracy without

a priori knowledge of shape of ID sources. Maximum likelihood (ML) approaches [

–

] have better

accuracy but require high computational complexity. The authors of [

] have taken the lead in

extending covariance matching estimation techniques (COMET) to DOA estimation of ID sources

using ULA. They have converted complex nonlinear optimization to two successive one-dimensional

(1D) searches utilizing the extended invariance principle (EXIP). Considering Gaussian and uniform

ID sources, number of sensors in experiment of [

] ranges from 4 to 20; they have proved that when

sensors is increased to a certain extent with other parameters ﬁxed, estimation tends to be less accurate.

Applying Taylor series expansion of steering vector to approximate the array covariance matrix

using the central moments of the source, the authors of [

] have elaborated a lower computational

COMET for ID sources, which exhibits a good performance at low SNR based on ULA with 11 sensors.

The authors of [

] have presented the ambiguity problem of COMET-EXIP algorithm using ULA and

proposed an inequality constraint in the original objective functions to solve this problem. The authors

of [

] have turned covariance matching problem to retrieve parameters of received covariance by

exploiting the annihilating property of linear nested arrays. The authors of [

] have embedded

algorithm of [19] into a Kalman ﬁlter for DOA tracking problem of ID sources.

The aforementioned DOA estimations of ID sources consider the sources and receive arrays are

in the same plane where sources are described by 1D model with two parameters: nominal angle

and angular spread. Generally, sources are in different plane with receive arrays, which should

be modeled as two-dimensional (2D) models with parameters as nominal azimuth angle, nominal

elevation angle, azimuth spread, and elevation spread. With more parameters, there have been

relatively few studies on estimation of 2D ID sources. The authors of [

] have extended COMET

algorithm to 2D scenarios, which separates variables of each source based on alternating projection

technique, then formulate equations set of unknown variables. The algorithm from [

] is applicable

to any arrays in three-dimensional spaces but requires considerably high computational complexity.

In addition, experiments of [

] have only considered a relatively small number of targets. The authors

of [

] have proposed a two-stage approach based on rotation invariance relations of generalized

steering vector of double parallel uniform linear arrays (DPULA), where nominal elevation is ﬁrstly

estimated via TLS-ESPRIT, then nominal azimuth is acquired by 1D searching.

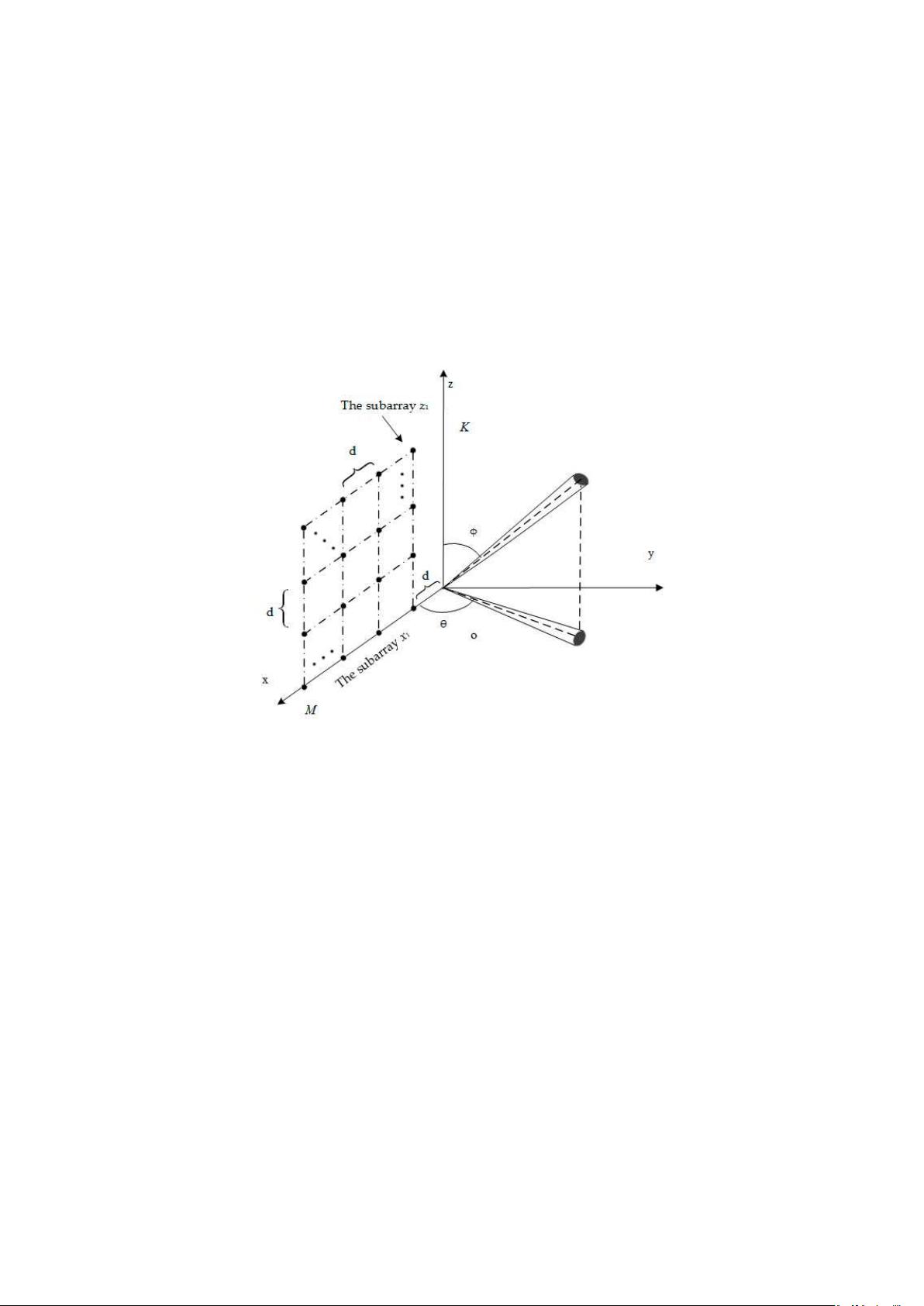
In order to estimate DOA of 2D ID sources, we propose an algorithm based on URA. Through

Taylor series expansions of steering vectors, received signal vectors of arrays can be expressed as a

generalized form which is combination of generalized steering matrix and generalized signal vector

under the assumption of small distance of sensors and small angular spread. Consequently, the rotation

invariance relations of constructed subarrays with respect to nominal azimuth and nominal elevation

are derived. Constructed subarrays fully use elements of URA, so the estimation accuracy is improved.

Then the nominal azimuth and nominal elevation can be calculated respectively by means of an ESPRIT

like algorithm. Thus, estimation of multiple 2D ID sources do not need spectral searching and avoid

high computational complexity. Lastly, the angle matching method is proposed according to Capon

Sensors 2018, 18, 3600 3 of 18

spectral search. Without information of angular power distribution function, the proposed method

can detect sources with different angular power distribution functions.

2. Arrays Conﬁguration and Signal Model

As shown in Figure 1, the URA consists of M

K sensors on xoz plane. The distance between

sensors along the direction of x and z axes is set at d meters. Azimuth

and elevation

are used to

describe the direction of signal in a three dimensional space. There are q 2D ID narrowband sources

with nominal angles (

) (i = 1, 2,

. . .

, q) denoting nominal azimuth and nominal elevation of the

ith sources impinging into arrays.

∈

[

0, π

]

∈

[

0, π

]

is the wavelength of the impinging signal.

The additive noise is considered as Gaussian white with zero mean and uncorrelated with sensors.

Sensors 2018, 18, x FOR PEER REVIEW 4 of 18

Figure 1. Uniform rectangular arrays configuration.

The M × 1 dimensional received vector of the kth subarray parallel to x-axis, which is defined as

subarray x

k, can be written as

() ( , ) ( , ,) ()

kki xk

t θφs θφtdθdφ t





x α n

(6)

where α

k(θ,φ) denotes the steering vector of subarray xk with respect to point source, which can be

written as

()cos/

(,) (,)

j π kd φλ

θφ θφe

−

=αα

(7)

The M × K dimensional received matrix of the URA along the x-axis can be expressed as

() [ (), (), , ()]=Xxx x

ttt t

(8)

The K × 1 dimensional received vector of the K sensors with distance d and parallel to z-axis

defined as subarray z

1 can be written as

11 1

() ( , ) ( , ,) ()

t θφs θφtdθdφ t





z β n

(9)

where the K × 1 dimensional vector β

1(θ,φ) denotes the steering vector of subarray z1 with respect to

point source, n

z1(t) denotes the noise vector of subarray z1. β1(θ,φ) can be expressed as

2221

cos sin / cos / ( ) cos /

(, ) , , ,

−





β 

j πd θφλ j πd φλ j π Kd φλ

θφ eee

(10)

The K × 1 dimensional received vector of the mth subarray parallel to z-axis defined as subarray

m can be written as

() ( , ) ( , ,) ()

mmi zm

t θφs θφtdθdφ t





z β n

(11)

where β

m(θ,φ) denotes the steering vector of subarray zm with respect to point source, which can be

written as

()cossin/

(,) (, )

j π md θφλ

θφ θφe

−

=ββ

(12)

The K × M dimensional received matrix of the URA along the z-axis can be expressed as

Figure 1. Uniform rectangular arrays conﬁguration.

The M

1 dimensional received vector of the M sensors located on the

-axis deﬁned as subarray

can be written as

(t) =

∑

i=1

(θ, ϕ)s

(θ, ϕ, t)dθdϕ + n

(t), (1)

where

(t) denotes the noise vector of subarray. The M

1 dimensional vector

(

) denotes the

steering vector of subarray x

with respect to point source, which can be expressed as

(θ, ϕ) =

j2πd cos θ sin ϕ/λ

, e

j2π2d cos θ sin ϕ/λ

, ··· , e

j2πMd cos θ sin ϕ/λ

, (2)

(

,t) is the complex random angular signal density of the distributed source representing the

reﬂection intensity of the source from angle (

) at the snapshot index t. Unlike a point source,

signal of a distributed source exists not only in the direction of (

) but also in a spatial distribution

around (

). A distributed source is deﬁned as incoherently distributed if s

(

,t) from one direction

is uncorrelated with other directions, which can be modeled as a random process as

E [s

(θ, ϕ, t)s

∗

(θ

, ϕ

, t)] = P

(θ, ϕ; u)δ(θ − θ

)δ(ϕ − ϕ

), (3)

where

(

) is the Kronecker delta function, P

is the power of the source, f

(

;

) is its normalized

angular power density function (APDF) reﬂecting geometry and surface property of a distributed

source. APDF is determined by parameter set

. For a Gaussian ID source,

= [

θi

φi

]

剩余17页未读，继续阅读

评论收藏

内容反馈

weixin_38590685

粉丝: 3
资源: 920

Two-Dimensional DOA Estimation for Incoherently Distributed Sour...

最新资源

Two-Dimensional DOA Estimation for Incoherently Distributed Sour...

&nbsp;均匀圆阵部分阵元失效情况下的DOA估计方法

二维DOA估计程序_DOA估计_matlab

doa估计算法

DOAestimation_DOA_

DOA算法程序

MUSIC and maximum likelihood techniques on two-dimensional DOA estimation

Two-Dimensional DOA Estimation for 5G Networks

（part3）Two-dimensional phase unwrapping: theory, algorithms, and software3

Two-dimensional signal and image processing.zip

Apress.PHP.Arrays.Single.Multi-dimensional.Associative.and.Object.Arrays.

Two-Dimensional Phase Unwrapping Problem

The two-dimensional Ising model (2014).pdf

Two-dimensional-code.zip_MATLAB二维码_two-dimensional-code_二维码 mat

Parallelizing Two-dimensional FFTs.pdf

Low-Dimensional Models for High-Dimensional Data From Linear to

Two-Dimensional FastFourier Transform

A Two-Dimensional Bar Code Reader

A two-dimensional hybrid for elastic-plastic stress analysis

C语言-二维数组two-dimensional-array-master.zip

High-dimensional data analysis with low-dimensional models-2020.pdf

PHP.Arrays.in.PHP.7

Image-classification-by-a-Two-Dimensional-Hidden-_two-dimensiona

High-Dimensional Probability: An Introduction with Applications in Data Science

Two-Dimensional Signal and Image Processing Part 2

Two-Dimensional Signal and Image Processing Part 1

Two-dimensional fast Fourier transform - Signal Processing

最新资源

均匀圆阵部分阵元失效情况下的DOA估计方法